# 1254. Number of Closed Islands
###### tags: `leetcode`
## Description
Given a 2D grid consists of 0s (land) and 1s (water). An island is a maximal 4-directionally connected group of 0s and a closed island is an island totally (all left, top, right, bottom) surrounded by 1s.

Return the number of closed islands.

- Example 1:

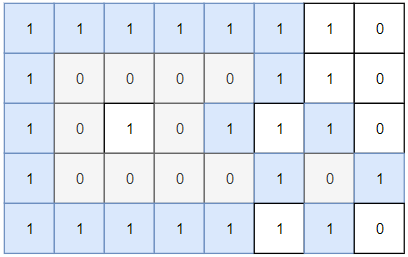
>Input: grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
Output: 2
>>Explanation:
Islands in gray are closed because they are completely surrounded by water (group of 1s).

- Example 2:

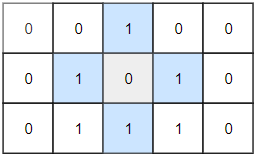
>Input: grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]]
Output: 1

- Example 3:

>Input: grid = [[1,1,1,1,1,1,1],
[1,0,0,0,0,0,1],
[1,0,1,1,1,0,1],
[1,0,1,0,1,0,1],
[1,0,1,1,1,0,1],
[1,0,0,0,0,0,1],
[1,1,1,1,1,1,1]]
Output: 2

- Constraints:

>$1 \leq grid.length, grid[0].length \leq 100$
$0 \leq grid[i][j] \leq1$

## Solution
- This is a typical dfs problem
- Use an iteration to go through all the nodes and check the value of the node to see whether it is the land that has not been gone through. Go to dfs when this happens

for (int i = 0; i < h; i++)
{
    for (int j = 0; j < w; j++)
    {
        if (grid[i][j] == 0)
            if (dfs(i, j, grid)) ans++;
    }
}

- When doing dfs, check the boundary problem because the land that reaches boundary can not be included. If it is not in the boundary case, go to the other sides to check the continuous land expansion

if (i == 0) closed = false;
else if (grid[i - 1][j] == 0) closed &= dfs(i - 1, j, grid);
if (i == h - 1) closed = false;
else if (grid[i + 1][j] == 0) closed &= dfs(i + 1, j, grid);
if (j == 0) closed = false;
else if (grid[i][j - 1] == 0) closed &= dfs(i, j - 1, grid);
if (j == w - 1) closed = false;
else if (grid[i][j + 1] == 0) closed &= dfs(i, j + 1, grid);

- The reason of using `&=` operation is that it can relay the boundary check previously and also go to the land even after the boudary check is confirmed