# 1697. Checking Existence of Edge Length Limited Paths
###### tags: `leetcode`
## Description
An undirected graph of n nodes is defined by edgeList, where edgeList[i] = [ui, vi, disi] denotes an edge between nodes ui and vi with distance disi. Note that there may be multiple edges between two nodes.

Given an array queries, where queries[j] = [pj, qj, limitj], your task is to determine for each queries[j] whether there is a path between pj and qj such that each edge on the path has a distance strictly less than limitj .

Return a boolean array answer, where answer.length == queries.length and the jth value of answer is true if there is a path for queries[j] is true, and false otherwise.

- Example 1:

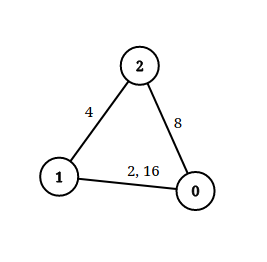
>Input: n = 3, edgeList = [[0,1,2],[1,2,4],[2,0,8],[1,0,16]], queries = [[0,1,2],[0,2,5]]
Output: [false,true]
>>Explanation: The above figure shows the given graph. Note that there are two overlapping edges between 0 and 1 with distances 2 and 16.
For the first query, between 0 and 1 there is no path where each distance is less than 2, thus we return false for this query.
For the second query, there is a path (0 -> 1 -> 2) of two edges with distances less than 5, thus we return true for this query.

- Example 2:

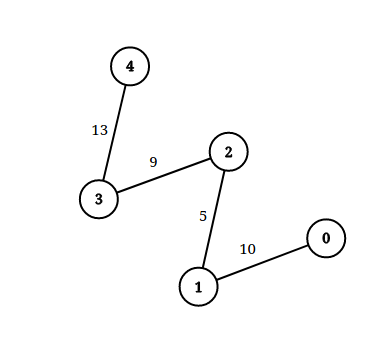
>Input: n = 5, edgeList = [[0,1,10],[1,2,5],[2,3,9],[3,4,13]], queries = [[0,4,14],[1,4,13]]
Output: [true,false]
>>Exaplanation: The above figure shows the given graph.

- Constraints:

>$2 \leq n \leq 10^5$
$1 \leq edgeList.length$, $queries.length \leq 10^5$
$edgeList[i].length == 3$
$queries[j].length == 3$
$0 \leq u_i, v_i, p_j, q_j \leq n - 1$
$u_i \neq v_i$
$p_j \neq q_j$
$1 \leq dis_i, limit_j \leq 10^9$
There may be multiple edges between two nodes.

## Solution
- The problem can be done by using `UnionSet`
- To begin with, sort the queries and edges by the value of them in order to keep the strictest one in the front. (In order to keep in the same sequence, the queries should keep the current index as well)

for (int i = 0; i < queries.size(); ++i) queries[i].push_back(i);
sort(begin(queries), end(queries), [&](auto &a, auto &b) { return a[2] < b[2]; });
sort(begin(edges), end(edges), [&](auto &a, auto &b) { return a[2] < b[2]; });

- In all the queries, connect the edges in the limit. Check the connectivity of the current result

for (auto &q : queries) { 
    int u = q[0], v = q[1], limit = q[2], qid = q[3];
    for (; i < edges.size() && edges[i][2] < limit; ++i) uf.connect(edges[i][0], edges[i][1]); 
    ans[qid] = uf.connected(u, v);
}

- In the `UnionSet`, connect the dot by finding the parent for the two nodes. Put the parent together if they are different

void connect(int a, int b) {
    int x = find(a), y = find(b);
    if (x == y) return;
    parent[x] = y;
}

- To check the connectivity, find he parents of the two

bool connected(int i, int j) { return find(i) == find(j); }

- To find the parent, check if they are the root, then recurse again and again

int find(int a) {
    return parent[a] == a ? a : (parent[a] = find(parent[a]));
}