# 547. Number of Provinces
###### tags: `leetcode`
## Description
There are n cities. Some of them are connected, while some are not. If city a is connected directly with city b, and city b is connected directly with city c, then city a is connected indirectly with city c.

A province is a group of directly or indirectly connected cities and no other cities outside of the group.

You are given an n x n matrix isConnected where isConnected[i][j] = 1 if the ith city and the jth city are directly connected, and isConnected[i][j] = 0 otherwise.

Return the total number of provinces.

- Example 1:

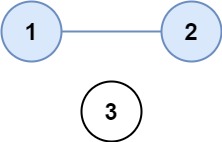
>Input: isConnected = [[1,1,0],[1,1,0],[0,0,1]]
Output: 2

- Example 2:

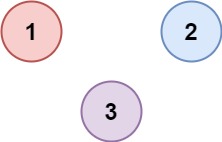
>Input: isConnected = [[1,0,0],[0,1,0],[0,0,1]]
Output: 3

- Constraints:

>1 <= n <= 200
n == isConnected.length
n == isConnected[i].length
isConnected[i][j] is 1 or 0.
isConnected[i][i] == 1
isConnected[i][j] == isConnected[j][i]

## Solution
- The problem can be solved by using DFS
- For each of the nodes, visit their connected dots by doing dfs from the point.

vector<int> visited(len);
int ans = 0;
for (int i = 0; i < len; i++)
{
    if (!visited[i])
    {
        ans++;
        dfs(i, len, isConnected, visited);
    }
}

- For the dfs procedure, mark the starting point as visited and start the iteration. Add all the connected dots into the queue and visit them if they have not been iterated yet

void dfs(int i, int n, vector<vector<int>>& isConnected, vector<int>&visited) {
    visited[i] = true;
    vector<int> adj;
    for (int j = 0; j < n; j++) if (isConnected[i][j]) adj.push_back(j);
    for (auto &j : adj) if (!visited[j]) dfs(j, n, isConnected, visited);
}