# 106. Construct Binary Tree from Inorder and Postorder Traversal
###### tags: `leetcode`
## Description
Given two integer arrays inorder and postorder where inorder is the inorder traversal of a binary tree and postorder is the postorder traversal of the same tree, construct and return the binary tree.

- Example 1:

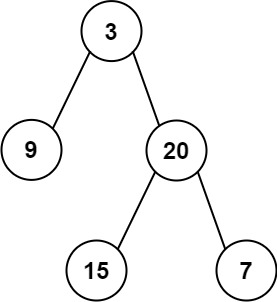
>Input: inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
Output: [3,9,20,null,null,15,7]

- Example 2:

>Input: inorder = [-1], postorder = [-1]
Output: [-1]

- Constraints:

>$1 \leq inorder.length \leq 3000$
postorder.length == inorder.length
$-3000 \leq inorder[i], postorder[i] \leq 3000$
inorder and postorder consist of unique values.
Each value of postorder also appears in inorder.
inorder is guaranteed to be the inorder traversal of the tree.
postorder is guaranteed to be the postorder traversal of the tree.

## Solution
- The key point to solve this problem is to compare the relationship between `inorder` and `postorder`
- The `inorder` takes left child, the value itself, and then the right child. The `postorder` takes left child, the right child, and then value itself
- The problem can be solved by looking into `postorder` first since we care about the actual `root` of the tree, which is bound to be the last element in the postorder

int temp = postl + len - 1; // last one in the postorder array
TreeNode* src = new TreeNode(postorder[temp]);
if (len == 1)
    return src;

- By looking into the value of the root in inorder, we can split the two chilren into left child and right child

auto it = find(inorder.begin() + inl, inorder.begin() + inl + len, postorder[temp]);

- The left child length can be told by the distance between the left of the tree and the root index

temp = (it - inorder.begin()) - inl;
if (temp != 0)
    src->left = buildSubTree(inorder, postorder, inl, postl, temp);

- The right child length and their left position can be updated by subtracting the left child and the root value

// inorder left index: add on left child length and the root space(1)
inl += temp + 1;
// postorder left index: add left child only because root space is on the right hand side
postl += temp;
// Right child length = total length - left child length - root space (1)
temp = len - temp - 1;
if (temp != 0)
    src->right = buildSubTree(inorder, postorder, inl, postl, temp);