# 802. Find Eventual Safe States
###### tags: `leetcode`
## Description
There is a directed graph of n nodes with each node labeled from 0 to n - 1. The graph is represented by a 0-indexed 2D integer array graph where graph[i] is an integer array of nodes adjacent to node i, meaning there is an edge from node i to each node in graph[i].

A node is a terminal node if there are no outgoing edges. A node is a safe node if every possible path starting from that node leads to a terminal node (or another safe node).

Return an array containing all the safe nodes of the graph. The answer should be sorted in ascending order.

- Example 1:

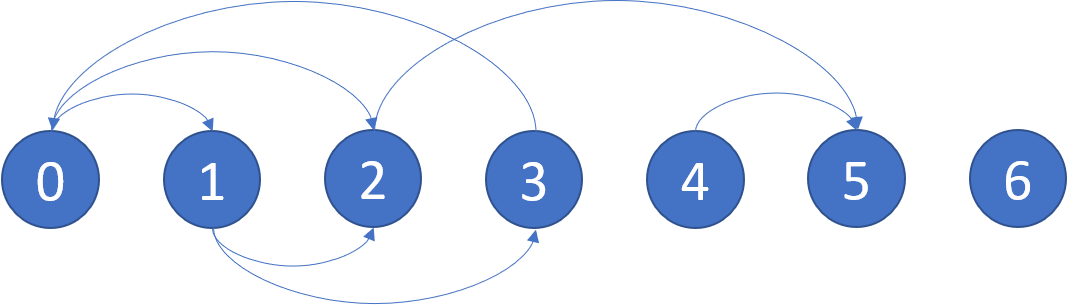
>Input: graph = [[1,2],[2,3],[5],[0],[5],[],[]]
Output: [2,4,5,6]
>>Explanation: The given graph is shown above.
Nodes 5 and 6 are terminal nodes as there are no outgoing edges from either of them.
Every path starting at nodes 2, 4, 5, and 6 all lead to either node 5 or 6.

- Example 2:

>Input: graph = [[1,2,3,4],[1,2],[3,4],[0,4],[]]
Output: [4]
>>Explanation:
Only node 4 is a terminal node, and every path starting at node 4 leads to node 4.

- Constraints:

>n == graph.length
1 <= n <= 104
0 <= graph[i].length <= n
0 <= graph[i][j] <= n - 1
graph[i] is sorted in a strictly increasing order.
The graph may contain self-loops.
The number of edges in the graph will be in the range [1, 4 * 104]

## Solution
- To make the question clear, there are two types of nodes we need to care about
- terminal node: no outgoing edge, the final stop
- safe node: all the outgoing edges points to safe node and terminal node
- As the result, use `bfs` to count the edges to answer and try to reverse the edges in order to backtrack the added safe nodes
- To begin with, record all the outgoing edges count

vector<int> out(graph.size()), ans;
vector<vector<int>> rev(graph.size());
queue<int> q;
for (int i = 0; i < graph.size(); i++)
{
    for (auto &j : graph[i]) rev[j].push_back(i);
    out[i] = graph[i].size();
    if (out[i] == 0) q.push(i);
}

- For all the nodes in queue, put them into answer vector and decrease all the starting points to it by 1 and check the outgoing count for all of them in order to add the edges

while (!q.empty())
{
    int cur = q.front();
    q.pop();
    ans.push_back(cur);
    for (auto &j : rev[cur]) if (--out[j] == 0) q.push(j);
}

- After all, sort the array and return it

sort(ans.begin(), ans.end());
return ans;