# 64. Minimum Path Sum
###### tags: `leetcode`
## Description
Given a `m x n` grid filled with non-negative numbers, find a path from top left to bottom right, which minimizes the sum of all numbers along its path.

Note: You can only move either down or right at any point in time.

Example 1:

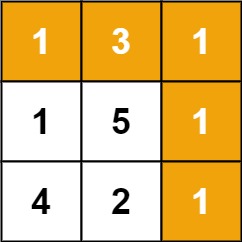
>Input: grid = [[1,3,1],[1,5,1],[4,2,1]]
Output: 7
>>Explanation: Because the path 1 → 3 → 1 → 1 → 1 minimizes the sum.

- Example 2:

>Input: grid = [[1,2,3],[4,5,6]]
Output: 12

- Constraints:

>m == grid.length
n == grid[i].length
$1 \leq m, n \leq 200$
$0 \leq grid[i][j] \leq 100$

## Solution
- The problem can be solved by using dynamic programming. To recurse for all the combination would bee a waste of time, so use an array to store all the information
- When the end is reached, just put the value in the dp set, and if it has only one direction left (either down or right), iterate to that direction

if (y == r)
{
    if (x == c) dp[y][x] = grid[y][x];
    else
    {
        if (grid[y][x + 1] != -1) minSubPathSum(grid, y, x + 1);
        dp[y][x] = grid[y][x] + dp[y][x + 1];
    }
}
else if (x == c)
{
    if (grid[y + 1][x] != -1) minSubPathSum(grid, y + 1, x);
    dp[y][x] = grid[y][x] + dp[y + 1][x];
}

- Else check the two direction if they are visited, go there and update the value. Choose the smaller one and update the table

else
{
    if (grid[y][x + 1] != -1) minSubPathSum(grid, y, x + 1);
    if (grid[y + 1][x] != -1) minSubPathSum(grid, y + 1, x);
    dp[y][x] = grid[y][x] + min(dp[y][x + 1], dp[y + 1][x]);
}

- After updating the value, turn itself as `-1`, showing that it is finished and the value can be straightly used

grid[y][x] = -1;