# 863. All Nodes Distance K in Binary Tree
###### tags: `leetcode`
## Description
Given the root of a binary tree, the value of a target node target, and an integer k, return an array of the values of all nodes that have a distance k from the target node.

You can return the answer in any order.

- Example 1:

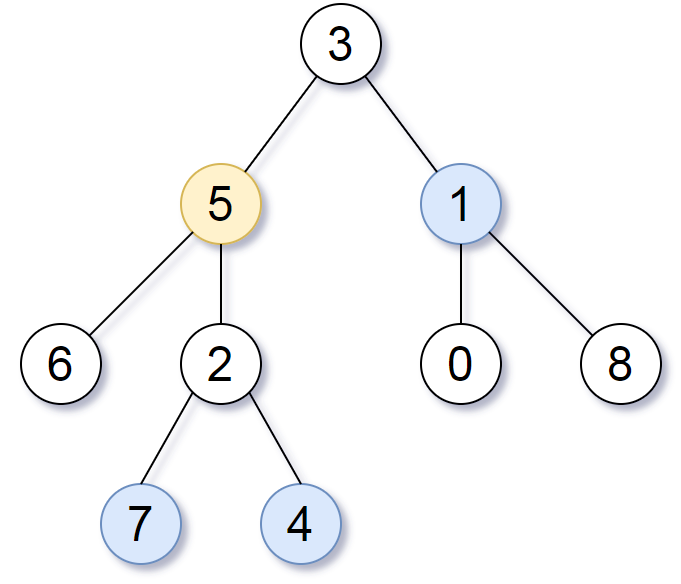
>Input: root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, k = 2
Output: [7,4,1]
>>Explanation: The nodes that are a distance 2 from the target node (with value 5) have values 7, 4, and 1.

- Example 2:

>Input: root = [1], target = 1, k = 3
Output: []

- Constraints:

>The number of nodes in the tree is in the range [1, 500].
0 <= Node.val <= 500
All the values Node.val are unique.
target is the value of one of the nodes in the tree.
0 <= k <= 1000

## Solution
- The problem can be categorized as follow
- The path that goes directly down
- The path that goes up for some steps and then go down
- The path that goes directly up
- Because we need to know how to go up, use a search to find the path from the root to the target

vector<TreeNode*> path;
rootToNodePath(root, path, target);

- In the `rootToNodePath`, we get the path from root and gradually down to the target. If the current path does not have target, we need to pop ip up

bool rootToNodePath(TreeNode* node, vector<TreeNode*> &path, TreeNode* target){
    if (node == NULL) return false;
    path.push_back(node);
    if (node == target) return true;
    if (rootToNodePath(node->left, path, target) || rootToNodePath(node->right, path, target)) return true;
    path.pop_back();
    return false;
}

- For the computational convinence, we reverse the path and start the iteration down with the step count degrading step by step

TreeNode* blocker = NULL;
vector<int> ans;
for (int i = 0; i < path.size(); i++)
{
    getNodes(path[i], k - i, ans, blocker);
    blocker = path[i];
}