# 1569. Number of Ways to Reorder Array to Get Same BST
###### tags: `leetcode`
## Description
Given an array nums that represents a permutation of integers from 1 to n. We are going to construct a binary search tree (BST) by inserting the elements of nums in order into an initially empty BST. Find the number of different ways to reorder nums so that the constructed BST is identical to that formed from the original array nums.

For example, given nums = [2,1,3], we will have 2 as the root, 1 as a left child, and 3 as a right child. The array [2,3,1] also yields the same BST but [3,2,1] yields a different BST.
Return the number of ways to reorder nums such that the BST formed is identical to the original BST formed from nums.

Since the answer may be very large, return it modulo 109 + 7.

- Example 1:

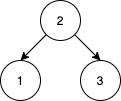
>Input: nums = [2,1,3]
Output: 1
>>Explanation: We can reorder nums to be [2,3,1] which will yield the same BST. There are no other ways to reorder nums which will yield the same BST.

- Example 2:

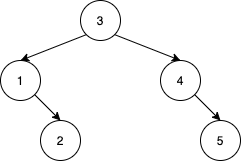
>Input: nums = [3,4,5,1,2]
Output: 5
>>Explanation: The following 5 arrays will yield the same BST:
[3,1,2,4,5]
[3,1,4,2,5]
[3,1,4,5,2]
[3,4,1,2,5]
[3,4,1,5,2]

- Example 3:

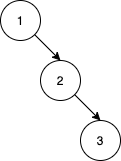
>Input: nums = [1,2,3]
Output: 0
>>Explanation: There are no other orderings of nums that will yield the same BST.

- Constraints:

>1 <= nums.length <= 1000
1 <= nums[i] <= nums.length
All integers in nums are distinct.

## Solution
- The problem can be done by using `DFS`.
- The main logic is clear. The first element must be the root, and the following nodes can be dividied as right (larger ones) and left (smaller ones)

for (; i < nums.size(); i++) {
    if (nums[i] < nums[0]) left.push_back(nums[i]);
    else right.push_back(nums[i]);
}

- For the result of the occurance, the calculate method is $C^{a+b}_{a}$ for $a=\text{left length}$ and $b=\text{right length}$. So calculate the value

for (i = b + 1; i <= a + b; i++) res = res * i % mod;
for (i = 2; i <= a; i++) res = res * inverse(i) % mod;

- The `inverse` is the divide part.

long inverse (long num) {
    if (num == 1) return 1;
    return mod - mod / num * inverse(mod % num) % mod;
}

- Finally, multiply the possibilities for both the left and right side

return res * dfs(left) % mod * dfs(right) % mod;