# 2218. Maximum Value of K Coins From Piles
###### tags: `leetcode`
## Description
There are `n` **piles** of coins on a table. Each pile consists of a **positive number** of coins of assorted denominations.

In one move, you can choose any coin on top of any pile, remove it, and add it to your wallet.

Given a list `piles`, where `piles[i]` is a list of integers denoting the composition of the `ith` pile from **top to bottom**, and a positive integer `k`, return the **maximum total value** of coins you can have in your wallet if you choose **exactly** k coins optimally.

- Example 1:

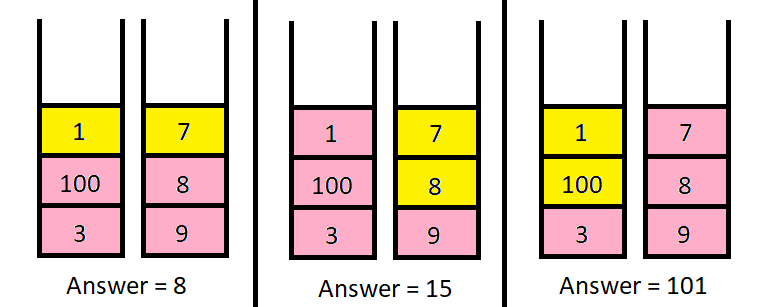
>Input: piles = [[1,100,3],[7,8,9]], k = 2
Output: 101
>>Explanation:
The above diagram shows the different ways we can choose k coins.
The maximum total we can obtain is 101.

- Example 2:

>Input: piles = [[100],[100],[100],[100],[100],[100],[1,1,1,1,1,1,700]], k = 7
Output: 706
>>Explanation:
The maximum total can be obtained if we choose all coins from the last pile.

- Constraints:

>n == piles.length
$1 \leq n \leq 1000$
$1 \leq piles[i][j] \leq 10^5$
$1 \leq k \leq sum(piles[i].length) <= 2000$

## Solution
- The problem is a dynamic programming issue and it requires heavier calculation
- To calculate the `k` coins with `n` piles, we can start with subpiles and subchoices
- The choice for the subpile can start with only one pile. The k choices can be done by accumulating the pile value till no elements are left

for (i = 1; i <= k; i++) dp[0][i] = (piles[0].size() >= i) ? dp[0][i - 1] + piles[0][i - 1] : dp[0][piles[0].size()];

- Later, when there are new piles adding in, we can see how many items can be joined, and find the maximum for each combination
- The maximum amount of the elements to join is the smaller value of the new added piles size or the total coins to collect

maxTaken = min(j, int(piles[i].size()));

- When adding the new pile, check the combination for adding the new value by the accumulation of new pile and the original one for dp table

acc = 0;
for (l = 0; l < maxTaken; l++)
{
    acc += piles[i][l];
    dp[i][j] = max(dp[i][j], acc + dp[i - 1][j - 1 - l]);
}

- The final value is the total pile set and the total coins to select

return dp.back().back();