# 1372. Longest ZigZag Path in a Binary Tree
###### tags: `leetcode`
## Description
You are given the root of a binary tree.

A ZigZag path for a binary tree is defined as follow:

Choose any node in the binary tree and a direction (right or left).
If the current direction is right, move to the right child of the current node; otherwise, move to the left child.
Change the direction from right to left or from left to right.
Repeat the second and third steps until you can't move in the tree.
Zigzag length is defined as the number of nodes visited - 1. (A single node has a length of 0).

Return the longest ZigZag path contained in that tree.

- Example 1:

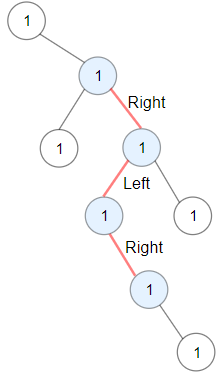
>Input: root = [1,null,1,1,1,null,null,1,1,null,1,null,null,null,1,null,1]
Output: 3
>>Explanation: Longest ZigZag path in blue nodes (right -> left -> right).

- Example 2:

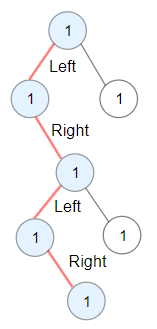
>Input: root = [1,1,1,null,1,null,null,1,1,null,1]
Output: 4
>>Explanation: Longest ZigZag path in blue nodes (left -> right -> left -> right).

- Example 3:

>Input: root = [1]
Output: 0

- Constraints:

>The number of nodes in the tree is in the range [1, 5 * 104].
$1 \leq Node.val \leq 100$

## Solution
- The problem can be regarded as a treversal issue
- To iterate and keepo the record for the biggest iteration value, the answer should be a global value and let the recursion go on for treversal

zz(root, true, 0);
zz(root, false, 0);
return ans;

- After so, check the existence of the current node and fo to the left and right to keep an eye on the maximum value. Only the correct order can plus the current value, unless it is a new set

if (!node) return;
ans = std::max(ans, currPathLen);
if (goLeft) {
    zz(node->left, false, currPathLen + 1);
    zz(node->right, true, 1);
} else {
    zz(node->right, true, currPathLen + 1);
    zz(node->left, false, 1);
}