# 1857. Largest Color Value in a Directed Graph
###### tags: `leetcode`
## Description
There is a **directed graph** of `n` colored nodes and `m` edges. The nodes are numbered from `0` to `n - 1`.

You are given a string `colors` where `colors[i]` is a lowercase English letter representing the **color** of the $i^{th}$ node in this graph (**0-indexed**). You are also given a 2D array `edges` where `edges[j] = [aj, bj]` indicates that there is a **directed edge** from node `aj` to node `bj`.

A valid path in the graph is a sequence of nodes `x1 -> x2 -> x3 -> ... -> xk` such that there is a directed edge from `xi` to `xi+1` for every `1 <= i < k`. The **color value** of the path is the number of nodes that are colored the most **frequently** occurring color along that path.

Return the **largest color value** of *any valid path in the given graph, or `-1` if the graph contains a cycle*.

- Example 1:

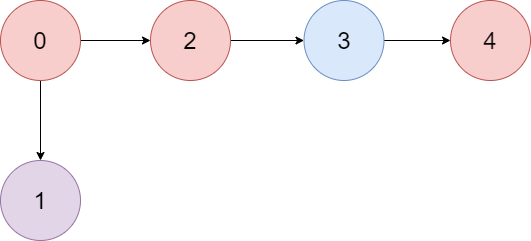
>Input: colors = "abaca", edges = [[0,1],[0,2],[2,3],[3,4]]
Output: 3
>>Explanation: The path 0 -> 2 -> 3 -> 4 contains 3 nodes that are colored "a" (red in the above image).

- Example 2:

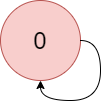
>Input: colors = "a", edges = [[0,0]]
Output: -1
>>Explanation: There is a cycle from 0 to 0.

- Constraints:

>n == colors.length
m == edges.length
$1 \leq n \leq 10^5$
$0 \leq m \leq 10^5$
colors consists of lowercase English letters.
$0 \leq a_j, b_j < n$

## Solution
- The problem is a `DFS` problem which contains lots of different twist
- To begin with, we need to find the begining of the path. Categorize the graph and find the in-direction edge counts

vector<int> indegrees(n, 0);
vector<vector<int>> graph(n, vector<int>());
for (vector<int>& edge : edges) {
    int u = edge[0];
    int v = edge[1];
    graph[u].push_back(v);
    indegrees[v]++;
}
unordered_set<int> zero_indegree;
for (int i = 0; i < n; i++) {
    if (indegrees[i] == 0) {
        zero_indegree.insert(i);
    }
}

- For each of the starting nodes, initialize the color counting vector

vector<vector<int>> counts(n, vector<int>(k, 0));
for (int i = 0; i < n; i++) {
    counts[i][colors[i] - 'a']++;
}

- We keep crack of `visited` count because for a looped graph, the `visited` count would be greater than all the number of the nodes.
- For all the starting points of the nodes that do not have in-directional edges, we iterate through them and refresh the count by adding for the maximum of the count
- After dealing with the edge, erase it by decreasing the count of the in-directional count of the incoming node. Check whether it still has other incominig edges, add to iteration if none is left
- Keep crack of the `max_count` for the maximum of the current one or the new updated node record

int max_count = 0;
int visited = 0;
while (!zero_indegree.empty()) {
    int u = *zero_indegree.begin();
    zero_indegree.erase(u);
    visited++;
    for (int v : graph[u]) {
        for (int i = 0; i < k; i++) {
            counts[v][i] = max(counts[v][i], counts[u][i] + (colors[v] - 'a' == i ? 1 : 0));
        }
        indegrees[v]--;
        if (indegrees[v] == 0) {
            zero_indegree.insert(v);
        }
    }
    max_count = max(max_count, *max_element(counts[u].begin(), counts[u].end()));
}

- When returning, compare the `visited` value because of the loop, which will result in more visited record

return visited == n ? max_count : -1;