# 1466. Reorder Routes to Make All Paths Lead to the City Zero
###### tags: `leetcode`
## Description
There are `n` cities numbered from `0` to `n - 1` and `n - 1` roads such that there is only one way to travel between two different cities (this network form a tree). Last year, The ministry of transport decided to orient the roads in one direction because they are too narrow.

Roads are represented by `connections` where `connections[i] = [ai, bi]` represents a road from city `ai` to city `bi`.

This year, there will be a big event in the capital (city `0`), and many people want to travel to this city.

Your task consists of reorienting some roads such that each city can visit the city `0`. Return the minimum number of edges changed.

It's **guaranteed** that each city can reach city `0` after reorder.

- Example 1:

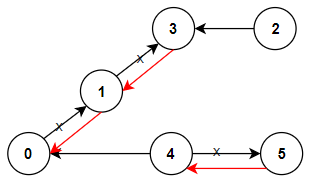
>Input: n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]
Output: 3
>>Explanation: Change the direction of edges show in red such that each node can reach the node 0 (capital).

- Example 2:

>Input: n = 5, connections = [[1,0],[1,2],[3,2],[3,4]]
Output: 2
>>Explanation: Change the direction of edges show in red such that each node can reach the node 0 (capital).

- Example 3:

>Input: n = 3, connections = [[1,0],[2,0]]
Output: 0

- Constraints:

>$2 \leq n \leq 5 \times 10^4$
connections.length == n - 1
connections[i].length == 2
$0 \leq a_i, b_i \leq n - 1$
$a_i != b_i$

## Solution
- The peoblem can be subdivided into the `DFS` tree structure
- Because it is a connected graph, we need to consider the direction of the tree and observe different behaviors
- For the root, if the node is pointing to the root, there is no need to change its direction. But if the node is pointing from the root, the direction should be turned around
- In order to store the direction value, construct two struvture to store the two direction of road and record the stamp for whether it has been visited

visit.resize(n);
to.resize(n);
from.resize(n);
for (auto &i : connections)
{
    to[i[0]].push_back(i[1]);
    from[i[1]].push_back(i[0]);
}

- When doing dfs, check the two direction and whether the node is visited, add when the direction is pointing outward and do the dfs

void dfs(int n) {
    visit[n] = true;
    for (auto &i : to[n])
    {
        if (!visit[i])
        {
            ans++;
            dfs(i);
        }
    }
    for (auto &i : from[n])
        if (!visit[i])
            dfs(i);
}