# 2101. Detonate the Maximum Bombs
###### tags: `leetcode`
## Description
You are given a list of bombs. The range of a bomb is defined as the area where its effect can be felt. This area is in the shape of a circle with the center as the location of the bomb.

The bombs are represented by a 0-indexed 2D integer array bombs where bombs[i] = [xi, yi, ri]. xi and yi denote the X-coordinate and Y-coordinate of the location of the ith bomb, whereas ri denotes the radius of its range.

You may choose to detonate a single bomb. When a bomb is detonated, it will detonate all bombs that lie in its range. These bombs will further detonate the bombs that lie in their ranges.

Given the list of bombs, return the maximum number of bombs that can be detonated if you are allowed to detonate only one bomb.

- Example 1:

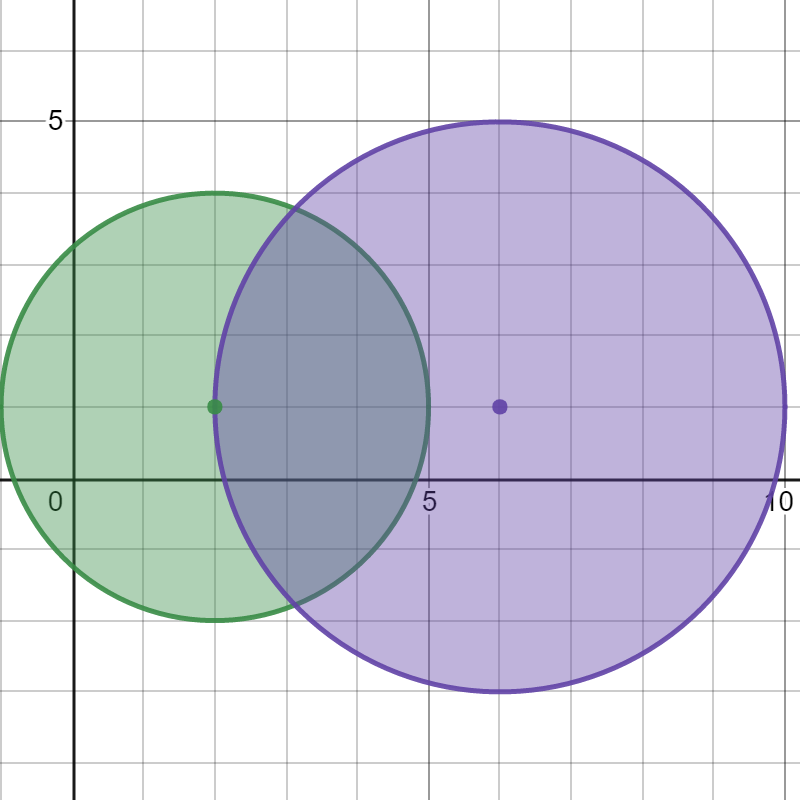
>Input: bombs = [[2,1,3],[6,1,4]]
Output: 2
>>Explanation:
The above figure shows the positions and ranges of the 2 bombs.
If we detonate the left bomb, the right bomb will not be affected.
But if we detonate the right bomb, both bombs will be detonated.
So the maximum bombs that can be detonated is max(1, 2) = 2.

- Example 2:

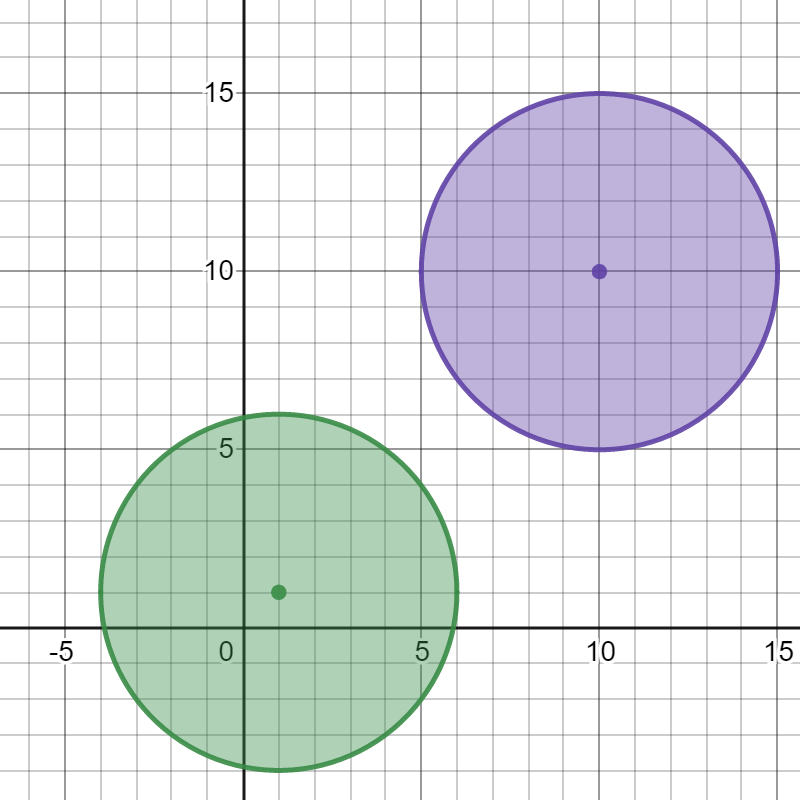
>Input: bombs = [[1,1,5],[10,10,5]]
Output: 1
>>Explanation:
Detonating either bomb will not detonate the other bomb, so the maximum number of bombs that can be detonated is 1.

- Example 3:

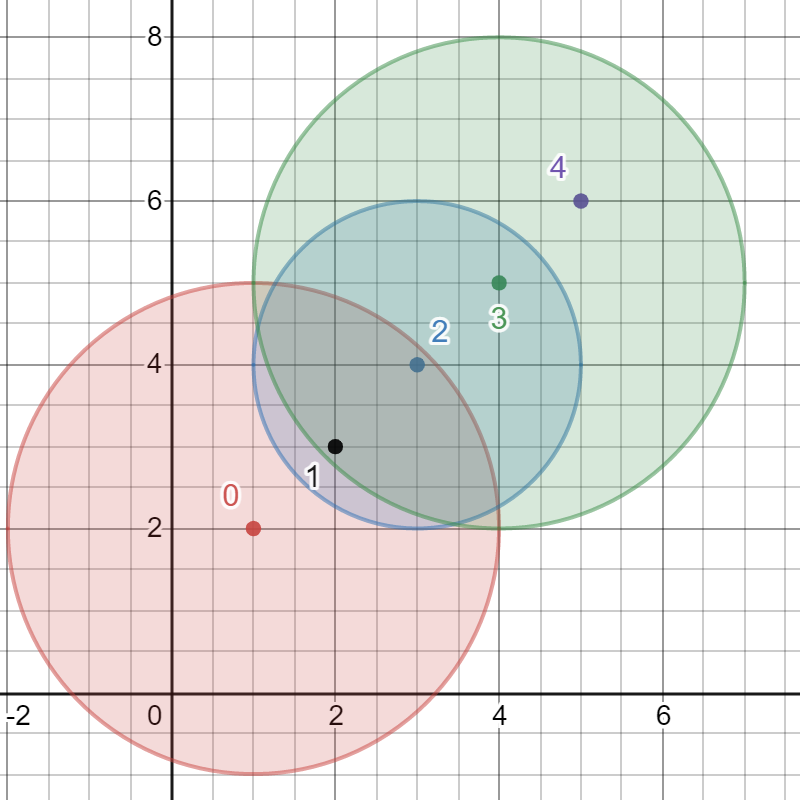
>Input: bombs = [[1,2,3],[2,3,1],[3,4,2],[4,5,3],[5,6,4]]
Output: 5
>>Explanation:
The best bomb to detonate is bomb 0 because:
- Bomb 0 detonates bombs 1 and 2. The red circle denotes the range of bomb 0.
- Bomb 2 detonates bomb 3. The blue circle denotes the range of bomb 2.
- Bomb 3 detonates bomb 4. The green circle denotes the range of bomb 3.
Thus all 5 bombs are detonated.

- Constraints:

>1 <= bombs.length <= 100
bombs[i].length == 3
1 <= xi, yi, ri <= 105

## Solution
- The problem is a revision of DFS. To cosntruct the relation graph, the edges are connected with direction if `the distance between the two nodes can cover the dimension of the initiated one`
- The distance can be calculated by iterating through all the possibilities of the two pairs in the set

vector<vector<bool>> graph(bombs.size(), vector<bool>(bombs.size()));
int i, j;
long long temp;
for (i = 0; i < bombs.size(); i++)
{
    for (j = i + 1; j < bombs.size(); j++)
    {
        temp = pow(bombs[i][0] - bombs[j][0], 2) + pow(bombs[i][1] - bombs[j][1], 2);
        graph[i][j] = temp <= pow(bombs[i][2], 2);
        graph[j][i] = temp <= pow(bombs[j][2], 2);
    }
}

- After the graph is constructed, iterate through all the nodes as the initiated bomb and see how many other bombs can be denotated as well by doing DFS starting from the first one. Record the largest one as the final answer

int ans = 1;
for (i = 0; i < bombs.size(); i++)
{
    vector<bool> stamp(bombs.size());
    int temp = 0;
    dfs(graph, i, stamp, temp);
    ans = max(ans, temp);
}

- The dfs function records all the iterated nodes by `stamp` vector. Mark as `finished` and append one to the count and then start the iteration for all the possible pathes

void dfs(vector<vector<bool>>& graph, int i, vector<bool>& stamp, int& ans) {
    stamp[i] = true;
    ans++;
    for (int j = 0; j < graph.size(); j++)
    {
        if (j == i) continue;
        if (graph[i][j] && !stamp[j]) dfs(graph, j, stamp, ans);
    }
}