# 662. Maximum Width of Binary Tree
###### tags: `leetcode`
## Description
Given the root of a binary tree, return the maximum width of the given tree.

The maximum width of a tree is the maximum width among all levels.

The width of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end-nodes that would be present in a complete binary tree extending down to that level are also counted into the length calculation.

It is guaranteed that the answer will in the range of a 32-bit signed integer.

- Example 1:

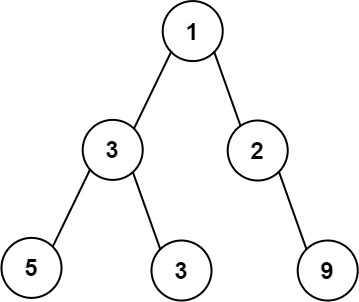
>Input: root = [1,3,2,5,3,null,9]
Output: 4
>>Explanation: The maximum width exists in the third level with length 4 (5,3,null,9).

- Example 2:

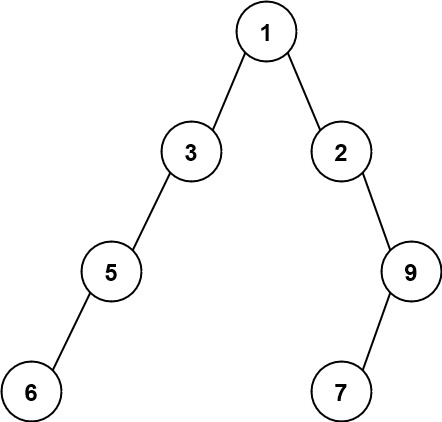
>Input: root = [1,3,2,5,null,null,9,6,null,7]
Output: 7
>>Explanation: The maximum width exists in the fourth level with length 7 (6,null,null,null,null,null,7).

- Example 3:

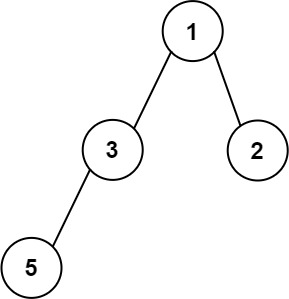
>Input: root = [1,3,2,5]
Output: 2
>>Explanation: The maximum width exists in the second level with length 2 (3,2).

- Constraints:

>The number of nodes in the tree is in the range [1, 3000].
-100 <= Node.val <= 100

## Solution
- To do the task, the BFS can be used with the index of the node
- Because it is a binary tree, there are at most 2 children. We can use the `2 * (parent) + 1/2` as the index for the children in avoidance of collision
- Keep track of the left most node and the right most node. The distance should be the distance between the two

sz = q.size();
a1 = 0, b1 = 0;
mn = q.front().second;
for(i = 0; i < sz; i++)
{
    auto p = q.front();
    TreeNode* b = p.first;
    long long int k = p.second - mn;
    q.pop();
    if(i == 0) a1 = k;
    if(i == sz - 1) b1 = k;

    if(b->left) q.push({b->left, 2 * k + 1});
                
    if(b->right) q.push({b->right, 2 * k + 2});
}

- The distance can be updated in each iteration

ans = max(ans, b1 - a1 + 1);