# 1579. Remove Max Number of Edges to Keep Graph Fully Traversable
###### tags: `leetcode`
## Description
Alice and Bob have an undirected graph of n nodes and three types of edges:

Type 1: Can be traversed by Alice only.
Type 2: Can be traversed by Bob only.
Type 3: Can be traversed by both Alice and Bob.
Given an array edges where edges[i] = [typei, ui, vi] represents a bidirectional edge of type typei between nodes ui and vi, find the maximum number of edges you can remove so that after removing the edges, the graph can still be fully traversed by both Alice and Bob. The graph is fully traversed by Alice and Bob if starting from any node, they can reach all other nodes.

Return the maximum number of edges you can remove, or return -1 if Alice and Bob cannot fully traverse the graph.

- Example 1:

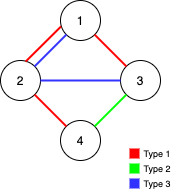
>Input: n = 4, edges = [[3,1,2],[3,2,3],[1,1,3],[1,2,4],[1,1,2],[2,3,4]]
Output: 2
>>Explanation: If we remove the 2 edges [1,1,2] and [1,1,3]. The graph will still be fully traversable by Alice and Bob. Removing any additional edge will not make it so. So the maximum number of edges we can remove is 2.

- Example 2:

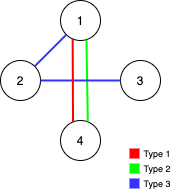
>Input: n = 4, edges = [[3,1,2],[3,2,3],[1,1,4],[2,1,4]]
Output: 0
>>Explanation: Notice that removing any edge will not make the graph fully traversable by Alice and Bob.

- Example 3:

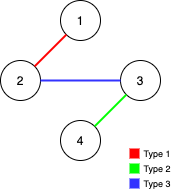
>Input: n = 4, edges = [[3,2,3],[1,1,2],[2,3,4]]
Output: -1
>>Explanation: In the current graph, Alice cannot reach node 4 from the other nodes. Likewise, Bob cannot reach 1. Therefore it's impossible to make the graph fully traversable.

- Constraints:

>1 <= n <= 105
1 <= edges.length <= min(105, 3 * n * (n - 1) / 2)
edges[i].length == 3
1 <= typei <= 3
1 <= ui < vi <= n
All tuples (typei, ui, vi) are distinct.

## Solution
- The problem can be done by using Union Set for each two
- To begin with, the edge for Type 3 is the most efficient one, so sort the edges by putting them in the front

sort(edges.begin(), edges.end(), [] (vector<int> &a, vector<int> &b) {return a[0] > b[0];});

- The problem can be eliminated to finding the fewest edges needed to be added in the system. Iterate through all the edges and see whether the edges needs to be added

UnionFind bob(n), alice(n);
for (auto &edge: edges) {
    int type = edge[0], one = edge[1], two = edge[2];
    switch (type) {
        case 3:
            edgesAdded += (bob.unite(one, two) | alice.unite(one, two));
            break;
        case 2:
            edgesAdded += bob.unite(one, two);
            break;
        case 1:
            edgesAdded += alice.unite(one, two);
            break;
    }
}

- Return the number of edges can be deleted or -1 if it is not connected

return (bob.united() && alice.united()) ? (edges.size()-edgesAdded) : -1;

- For the UnionSet, we need to keep the record for the distinct set count and all the parents

UnionFind(int n) {
    distinctComponents = n;
    for (int i = 0; i <= n; i++) {
        component.push_back(i);
    }
}

- The unite process is to find the original parents of the two. If they have the same parent, we do not need to add in the edge. In other case, one of them should be put into the other's parent tree and mark one edge required

bool unite(int a, int b) {
    if (findComponent(a) == findComponent(b)) {
        return false;
    }
    component[findComponent(a)] = b;
    distinctComponents--;
    return true;
}

- The process of `findComponent` is just the iteration till the root one

int findComponent(int a) {
    if (component[a] != a) {
        component[a] = findComponent(component[a]);
    }
    return component[a];
}

- To see whether all the nodes have beed iterated through, return the count of disjoint set

bool united() {
    return distinctComponents == 1;
}