# 2316. Count Unreachable Pairs of Nodes in an Undirected Graph
###### tags: `leetcode`
## Description
You are given an integer `n`. There is an undirected graph with `n` nodes, numbered from `0` to `n - 1`. You are given a 2D integer array edges where `edges[i] = [ai, bi]` denotes that there exists an undirected edge connecting nodes `ai` and `bi`.

Return the number of pairs of different nodes that are unreachable from each other.

- Example 1:

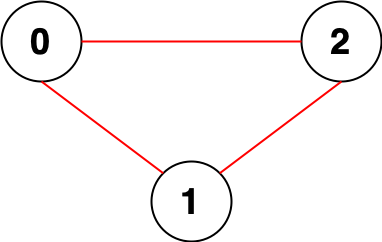
>Input: n = 3, edges = [[0,1],[0,2],[1,2]]
Output: 0
>>Explanation: There are no pairs of nodes that are unreachable from each other. Therefore, we return 0.

- Example 2:

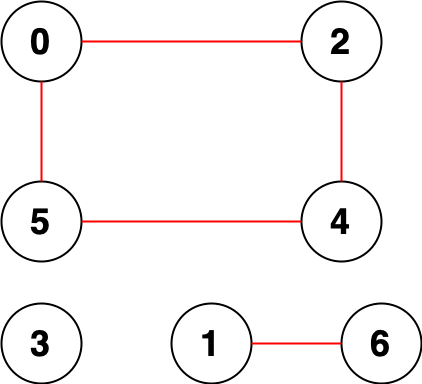
>Input: n = 7, edges = [[0,2],[0,5],[2,4],[1,6],[5,4]]
Output: 14
>>Explanation: There are 14 pairs of nodes that are unreachable from each other:
[[0,1],[0,3],[0,6],[1,2],[1,3],[1,4],[1,5],[2,3],[2,6],[3,4],[3,5],[3,6],[4,6],[5,6]].
Therefore, we return 14.

- Constraints:

>$1 \leq n \leq 10^5$
$0 \leq edges.length \leq 2 \times 10^5$
$edges[i].length == 2$
$0 \leq a_i, b_i < n$
$a_i \neq b_i$
There are no repeated edges.

## Solution
- The problem is to find the subset for each connected group
- By using `DFS`, we can simply group those connected graph together

void dfs(int i)
{
    if (visit[i] == 0)
    {
        ++cnt.back();
        visit[i] = 1;
        for (auto &j : graph[i])
            dfs(j);
    }
}

- Iterate through all the nodes and find the one that has not been iterated yet, dfs it

for (int i = 0; i < n; i++)
{
    if (visit[i] == 0)
    {
        cnt.push_back(0);
        dfs(i);
    }
}

- For those that only have one connected set, the cross cost is `0`, which is an exceptional case

if (cnt[0] == n) return 0;

- To count for each two sets, the trick is to group the other counted set together and count it for one time in avoidance of two for loop

long long int ans = 0, temp = 0;
for (int i = 0; i < cnt.size(); i++)
{
    ans += cnt[i] * (n - temp - cnt[i]);
    temp += cnt[i];
}
return ans;