# 2492. Minimum Score of a Path Between Two Cities
###### tags: `leetcode`
## Description
You are given a positive integer n representing n cities numbered from 1 to n. You are also given a 2D array roads where `roads[i] = [ai, bi, distancei]` indicates that there is a bidirectional road between cities ai and bi with a distance equal to distancei. The cities graph is not necessarily connected.

The score of a path between two cities is defined as the minimum distance of a road in this path.

Return the minimum possible score of a path between cities `1` and `n`.

- Note:
- A path is a sequence of roads between two cities.
- It is allowed for a path to contain the same road multiple times, and you can visit cities 1 and n multiple times along the path.
- The test cases are generated such that there is at least one path between 1 and n.

- Example 1:

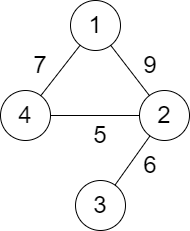
>Input: n = 4, roads = [[1,2,9],[2,3,6],[2,4,5],[1,4,7]]
Output: 5
>>Explanation: The path from city 1 to 4 with the minimum score is: $1 \leq 2 \leq 4$. The score of this path is min(9,5) = 5.
It can be shown that no other path has less score.

- Example 2:

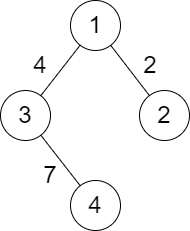
>Input: n = 4, roads = [[1,2,2],[1,3,4],[3,4,7]]
Output: 2
>>Explanation: The path from city 1 to 4 with the minimum score is: $1\leq 2\leq 1 \leq 3 \leq 4$. The score of this path is min(2,2,4,7) = 2.

- Constraints:

>$2 \leq n \leq 10^5$
$1 \leq roads.length \leq 10^5$
roads[i].length == 3$
$1 <= a_i, b_i <= n$
$a_i != b_i$
$1 \leq distance_i \leq 10^4$
There are no repeated edges.
There is at least one path between 1 and n.

## Solution
- The problem can be regarded as either `BFS` or `DFS` problem. Go through the iteration to find the iterated subset of the links that should be included in the graph
- To begin with, construct a graph that contain the road for each node and the corresponding value

vector<vector<int>> adj[n + 1];
for(int i = 0; i < roads.size(); i++)
{
    adj[roads[i][0]].push_back({roads[i][1],roads[i][2]});
    adj[roads[i][1]].push_back({roads[i][0],roads[i][2]});
}

- The visited stamp should be kept because it is crucial to see whether the node is actually connected with source 1 and destination n

vector<bool> vis(n + 1,false);
vis[1] = true;

- By using `BFS`, check all the nodes that are connected and collect it by pushing it into the queue

queue<int> q;
q.push(1);
while(!q.empty())
{
    int node = q.front();
    q.pop();
    for(auto &it : adj[node])
    {
        if(!vis[it[0]])
        {
            vis[it[0]] = true;
            q.push(it[0]);
        }
    }
}

- By checking the visited nodes, we can make sure which path is included and update the real answer

int ans = INT_MAX;
for(int i = 0; i < roads.size(); i++)
{
    if(vis[roads[i][0]] && vis[roads[i][1]])
        ans = min(ans,roads[i][2]);
}
return ans;