---
title: 樹 Tree
tags: article
---
---
# 結構(Structure)
二元樹的概念很簡單,就只是把原先Linked List的單一節點從單分支 變成 雙分支,
即樹的每個節點可以指向兩個子節點(children),其兩個子節點分別為左和右節點 (left & right)
```cpp
// the node structure of binary tree
class Node{
public:
int value;
Node *left;
Node *right;
};
```
 
(還記得老大第一堂課在黑板上畫的右邊那張圖嗎?這就是一個二元樹)
> 我們通常會以一些名詞來形容一棵樹,像是root(根)、leaf(葉)、level(層數)...等,
> 詳細名詞可以參見此講義:[資訊之芽2021算法班 - Tree](https://www.csie.ntu.edu.tw/~sprout/algo2021/ppt_pdf/week02/tree.pdf)
---
# 遍歷(Traversal)
主要使用兩種方式:<font color=blue>DFS(深度優先搜索)</font> 和 <font color=blue>BFS(廣度優先搜索)</font>
> 就普遍而言,大多情況都只會使用DFS,而不是BFS,
> 其原因是因為BFS寫法過於複雜,且通常會佔用更多的記憶體。
> ( DFS的記憶體用量 = 樹的深度、BFS的記憶體用量 = 當前層的數量 + 下一層的數量 )

- ## DFS (Depth-First Search) : 深度優先搜索
其檢查方式又分成三種形式:<font color=blue>preorder(前序)、inorder(中序)、postorder(後序)</font>
以此圖做舉例:

前序 = $\{3, 5, 6, 2, 7, 4, 1, 0, 8\}$
中序 = $\{6, 5, 7, 2, 4, 3, 0, 1, 8\}$
後序 = $\{6, 7, 4, 2, 5, 0, 8, 1, 3\}$
```cpp
void dfs(Node* ptr){
if(ptr == NULL) //end condition
return;
// preorder code here
dfs(ptr->right);
// inorder code here
dfs(ptr->left);
// postorder code here
}
```
- ## BFS (Breadth-First Search) : 廣度優先搜索

```cpp
void bfs(Node* head){
queue<Node*> buffer;
buffer.push(head);
while(!buffer.empty()){
if(buffer.front() != NULL){
buffer.push(buffer.front()->right);
buffer.push(buffer.front()->left);
cout << buffer.front()->value << '\n';
}
buffer.pop();
}
}
```
BFS即是將搜索的順序存起來(通常都會用queue來存),
並將存起來的順序由舊到新依序移出。
> queue是一個容器(Container),可以將其看成是一個「隊伍」的物件,
> push即排至隊伍尾端(push back),front是取出隊伍排頭的資料,pop是將隊伍排頭給移除。
>
> queue介紹:[C++ std::queue 用法與範例](https://shengyu7697.github.io/blog/2020/02/18/std-queue/)
---
# 各種樹(Variants of Tree)
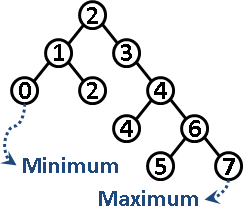
- ## 二分搜尋樹(Binary Search Tree)
小的往左放,大的往右放
---
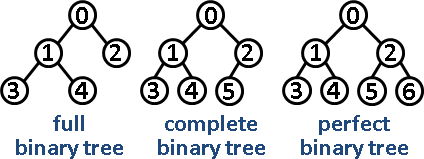
- ## Full Binary Tree、Complete Binary Tree、Perfect Binary Tree
**Full Binary Tree** : 每個節點皆有左右的子節點
**Complete Binary Tree** : 各層節點全滿,除了最底層的節點之外
**Perfect Binary Tree** : 每層節點皆滿
---
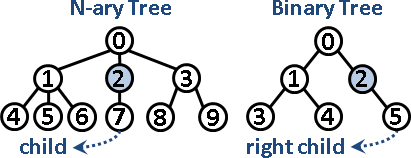
- ## N元樹(N-ary Tree)
每個節點有N個分支(N個子節點)
---
- ## 一維陣列存二元樹(Stored Binary Tree with 1D-Array)
利用一維陣列儲存二元樹的作法,其特性在於易於設計與編寫:
> 這種做法並不適合用來儲存一棵二元樹,可以想想為什麼
- 往左:left = root<<1
- 往右:right = (root<<1)+1

---
- ## 其他
wiki有個非常多的樹分類表,不用太擔心,幾乎大部分的樹都不會學到和用到。
wiki連結:[wiki - 樹 (資料結構)](https://zh.wikipedia.org/wiki/%E6%A0%91_(%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84))

---
文章參考:
- 資訊之芽2021算法班 - Tree : [(上篇)](https://www.csie.ntu.edu.tw/~sprout/algo2021/ppt_pdf/week02/tree.pdf)、[(下篇)](https://www.csie.ntu.edu.tw/~sprout/algo2021/ppt_pdf/week02/tree.pdf)
- [Geeks - Binary Tree Data Structure](https://www.geeksforgeeks.org/binary-tree-data-structure/)
- [演算法筆記 - Binary Tree](http://web.ntnu.edu.tw/~algo/BinaryTree.html)
---
# Problem Set
### Easy
1. LeetCode : [700. Search in a Binary Search Tree](https://leetcode.com/problems/search-in-a-binary-search-tree/)
2. LeetCode : [104. Maximum Depth of Binary Tree](https://leetcode.com/problems/maximum-depth-of-binary-tree/)
3. LeetCode : [938. Range Sum of BST](https://leetcode.com/problems/range-sum-of-bst/)
4. LeetCode : [965. Univalued Binary Tree](https://leetcode.com/problems/univalued-binary-tree/)
### Medium
1. 程式自學平台 : [[C_DT43-易] 嚴格二元樹](https://e-tutor.itsa.org.tw/e-Tutor/mod/programming/view.php?id=21770)
### Challenge
1. LeetCode : [102. Binary Tree Level Order Traversal](https://leetcode.com/problems/binary-tree-level-order-traversal/)
2. 程式自學平台 : [[C_DT26-中] 樹的走訪方式](https://e-tutor.itsa.org.tw/e-Tutor/mod/programming/view.php?id=13741)
3. Zerojudge : [d453. 最短距離](https://zerojudge.tw/ShowProblem?problemid=d453)
```
```
---
# Hints
### Easy
1. 利用Binary Search Tree的遍歷方式,當遇到相同值時即回傳該節點
2. 計算最大高度的遞迴式 : 1 + max( left_height, right_height )
3. 利用DFS遍歷樹的練習,此題意即判斷該節點的值落於區間之間
4. 判斷整棵樹的值是否皆相等
### Medium
1. 建構一棵二分搜尋樹,並判斷其是否為Full Binary Tree
### Challenge
1. 利用BFS,以樹的每層做分層,在兩層之間塞一個東西(作為分層用的判斷點),
或是記錄當前層的節點數量和下一層的節點數來判斷是否要換一層
2. 依照題意以BFS的方式建構一棵二元樹,並輸出該棵樹的preorder走訪順序
3. 迷宮走訪BFS,利用二維陣列紀錄有哪些格子是已經被走過或是不能走的,
其BFS所存的資料可以設成是一個座標點。
###### posted date: `2021.4.1`
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet