---
title: 'Notater'
disqus: hackmd
---

<style>
.markdown-body h1 {
font-size: 50px;
margin-top: 2em;
}
.markdown-body h2 {
font-size: 40px;
margin-top: 1.8em;
}
.markdown-body h3 {
font-size: 35px;
margin-top: 1.6em;
}
.markdown-body h4 {
font-size: 30px;
margin-top: 1.4em;
}
.markdown-body h5 {
font-size: 25px;
margin-top: 1.2em;
}
.markdown-body h6 {
font-size: 20px;
margin-top: 1em;
}
img {
padding: 1px;
border: solid black 1px;
}
.markdown-body blockquote {
margin-bottom: 3em;
}
</style>

# Datamaskinarkitektur notater

## Links
### Markdown & LaTeX
* [Mermaid Cheat-Sheet](https://jojozhuang.github.io/tutorial/mermaid-cheat-sheet/)
* [Latex Math Symbols](https://oeis.org/wiki/List_of_LaTeX_mathematical_symbols)
* [Markdown Cheat-Sheet](https://www.markdownguide.org/cheat-sheet)

# Table of Contents
[TOC]

# Kapittel 1 - Historie, Tallsystem og Basics
## Historie
Start:
- Kalkulator
- Rele
- Telefonsentraler

1947: Første transistor
1950-tallet: Første IC (Integrated circuit)

TRENGER MER INFO

## Tallsystem
### Dec system eksempel
$193_{10} \\ = 1*10^2+9*10^1+3*10^0 \\ = 1*100+9*10+3*1 \\ = 100+090+3 \\ = 193$

### Bin system
#### Bin --> Dec nr.1
$11000001_2 \\ = 1*2^0+0*2^1+0*2^2+0*2^3+0*2^4+0*2^5+1*2^6+1*2^7 \\ = 1*1+1*64+1*128 \\ = 1+64+128=1+64+128 = 193_{10}$

#### Bin --> Dec nr.2
$1011.01_2 \\ = 1*2^3+0*2^2+1*2^1+1*2^0+0*2^{-1}+1*2^{-2} \\ = 1*8+0*4+1*2+1*1+\frac{0}{2}+\frac{1}{4} \\ = 8+0+2+1+0+0.25 \\ = 11.25_{10}$

### Hexadesimale system
#### Bin --> Hex
$1000110001111101_2 \\ = 1000|1100|0111|1101 \\ = 8|12|7|13 \\ = 8|C|7|D \\ = 8C7D_{16} \\ = 0x8C7D$

#### Hex --> Bin
* $0x123 \\ = 1*16^2+2*16^1+3*16^0 \\ = 256+32+3 \\ = 291_{10}$

#### Dec --> Hex nr.1

  i) 193 : 16 = 12
     16
     ----
      33
      32
      ---
       1
    
  ii) 12 : 16 = 0
       0
      --
      12

| Kvotient | Rest |
| -------- | ---- |
| 12 | 1 |
| 0 | 12 |

==$=> 12 | 1 = 0xC1$==

#### Dec --> Hex nr.2

    i) 513 : 16 = 32
        48
       ---
        33
        32
        --
         1
      
   ii) 32 : 16 = 2
       32
       --
        0
       
  iii) 2 : 16 = 0
       0
       -
       2

| Kvotient | Rest |
| -------- | ---- |
| 32 | 1 |
| 2 | 0 |
| 0 | 2 |

==$=> 2|0|1 = 0x201$==

## Tallområde
Ulike verdier: $2^n$
Max verdier: $2^n-1$
Min verdi: 0

| Typer | Formel |
| --------- | ------------------------------------------------------------ |
| Unipolare | $s=[N_{min}, N_{max}] = [0, 2^n-1]$ |
| Bipolare | $s=[-\frac{1}{2}*2^n, +\frac{1}{2}*2^2-1] = [-2^{n-1}, +2^{n-1}-1]$ |

**Eks**
$n=10$
a) 0 - 5V
* Unipolart: $S=[0, 2^{10}-1]=[0, 1023]$
b) -2.5 - 2.5V
* Bipolart: $S=[-2^9, 2^9-1]=[-512, 511]$

## Klokkefrekvens
$t_{clock} = \frac{1}{f_{clock}}$

#### Eks
* $f_{clk} = 24MHz$
* $t_{clock} = 24MHz = \frac{1}{24''} = 0.00000004166666666666667 = 41.7*10^{-9} = 41.7ns$

## Hovedgrupper
- Generelle datamaskiner: PC, PLS
- Innebygde (embedded): mikrocontroller, vaskemaskin, ...

## Utviklingstrekk
* Integrasjon
* Kapasitet
* Gjerrige mikrokontrollere
* Selvforsynte komponenter
* Prisreduksjon

# Kapittel 2 - Mikroprosessor, CPU, Minneaddressering og Programmering
## Mikroprosessorbaserte system
> Mikroprosessoren kommuniserer med periferimodulene over systembussem, som er delt inn i:
* Databuss (8-64bit): Hva som skal overføres
* Adressebuss (16-64bit): Hvor skal dette overføres
* Styrebuss: Hvordan skal ting overføres
* *RD* - read, *WR* - write
* Adressedekoder: Leser addressen og velger den rette modulen.

## CPU-en
* Registerblokk: Brukes til å mellomlagre verdier som blir hentet fra minne eller kommer fra ALU-en
* ALU-en: Regner ut verdier
* Instruksjonsdekoderen: Forteller CPU-en hva den skal gjøre. For eksempel hvilke tall den skal plusse sammen osv.
* PC (Program Counter): Holder styr på hvilke "linje" CPU-en er på nå
* Tidtaking og styring "taktstokk": Holder "tiden"
* Statusregister (SR): # Antar den holder styring på om operasjonene var vellykket eller ikke, men ikke sikker. Bør søke opp
* Inn/ut- port: # Antar den brukes til å kommunisere med RAM osv. som ikke er i CPU-en

## Minne (registerblokk)
> Minnet har en lengde på 1 byte og høyde på n-bit. ARM CM3 har 32-bit med minne

### Minnestørrelse utregning:

     0xFFFFFFFF
  -  0x00000000
  +           1
  -------------
  = 0x100000000


  0x100000000 = 1*16^8 + 0*16^7 + ... + 0*16^0 
              = 1*16^8 
              = 1*(2^4)^8
              = 1*2^(4*8)
              = 1*2^32
              = 2^32
              = 2^2*2^30  // 2^30 = 1GB
              = 2^2 GB
              = 4 GB

> Forteller totalt størrelse på minne. Sier **ikke** hva maks addressen er.

## Omgjøring fra høynivå til lavnivå kode
> Forteller CPU-en hva den skal gjøre, steg for steg.

## Mikroprosessor operasjons gjennomgang

## Parallellkjøring

## Minnekart
Viser addresseområdet for ulike moduler i mikrokontrolleren

> Hele minnet deles opp i flere deler. Hver ting på mikrokontrolleren har sitt eget område på minnet.

## GPIO blokksjema
> Blokksjema av en GPIO modul (typisk periferimodul).
> GPIO modulen har et eget addresseringsområde i minnet. Man kan med C hente ut all informasjonen i minnet.

a = GPIOA --> ldr;
GPIOC --> odr = b;

*Ved bruk av GPIO må man konfigurere de ulike pinnene*
De ulike pinnene trenger:
* inngang
* utgang
* alteternativfunksjon (AF)
* Hvis man vil bruke en spesiell perifermodul så må man konfigurere pinnen på en spesiell måte så må signalene ha helt spesielle funksjoner

## Eksempel for lab 1

graph TD
    A((main)) --> B[init]
    B --> C{"while(1)"}
    C --> |Yes| D[Do something]
    D --> C

## Baseaddresse
Den minste addressen en modul kan ha

### Baseaddresse for en GPIO modul

## Grunnleggende struktur for en standard I/O prot bit

## Programmering av ARM
- Bruker **C**
- ARM har en programmvarestandard kalt **CMSIS**

### Datatyper
#### Heltall (Integers)
| Navn | Info |
| -------- | ---------------- |
| uint8_t | 8 bit (1 Byte) |
| int16_t | 16 bit (halvord) |
| uint32_t | 32 bit (ord) |

> Man trenger bare å referere til den *første* minne addressen. Prosessoren vet at hvis variable, for eksempel, er `uint32_t` å man henviser til minneaddressen til den første av de 4 cellene så vil den automatisk ta med de 3 som er over.

### Bitvise operasjoner
* $12 = 00001100$
* $25 = 00011001$

| Operator | Operator Navn | Forklaring | Eksempel | Kode Eksempel |
| -------- | --------------- | ---------- | -------- | ------------- |
| **&** | **AND** | Begge tallene må være `1`. ==Brukes til nullstilling (CLEAR)== |  |  |
| **\|** | **OR** | Ett av tallene må være `1`. ==Brukes til å sette en bit (Testing)== |  |  |
| **^** | **XOR** | `1` hvis *ulike*, `0` hvis like. ==Snuing av en bit==|  |  |
| **~** | **Complement (IKKE)** | Inverterer det binære tallet. ==Snuing av alle bit==|  | |
| **>>** | **Right Shift** | *Skifter* tallet n-hakk til høyre |  | |
| **<<** | **Left Shift** | *Skifter* tallet n-hakk til venstre |  | |

### Pekere (Pointer)
eks:

int8_t a=1,b,*P; // "*P" sier at *innholdet* i P er en 8 bit størrelse (1 byte)
p = &a; // Betyr at *p* er addressen til a (bilde 1 under)
b = *P; // Betyr at b = verdien som ligger i minneplasseringen til a som er 1


> P = minneplasseringen til *a* og siden *a* = 1 så blir verdien som *P* peker på `0x01` (0x01 = 1~10~)

### SysTick
Er en del av mikroprosessoren som brukes til å "telle". Den teller vanligvis ned fra en verdi og deretter sender et *avbrudd (interrupt)* signal når den har kommet til 0. Deretter starter den på nytt igjen.
>

> Viser gangen av systick. Starter på en tidsverdi. Teller til 0. Sender et *interrupt*. Starter på nytt.

$T_{int}=startverdi*t_{clk} = \frac{startverdi}{f_{clk}}$
eks:
* $T_{int} = \frac{72000}{72*10^6}=1*10^{-3}=1ms$
<br />

## Bygging av C-programmer
1. Høynivå kode:
> Høynivåkode med instruksjonssettet i assembly.
> Har en global variabel `int counter;`
> Har en funksjon `int counterInc(void)` som inkrementerer `counter`

2. Minnekart for STM32F103RB
3. Eksempeloppsett av minnekart under kjøring av `counterInc()`

    FLASH MINNE:

    |-------------|
    |             |
    |-------------|
    | int counter |
    |-------------| <-- Baseaddressen for å få verdien i *counter*
    |             |
    |-------------|
    | main()      |
    |-------------| <-- Baseaddressen for main()
    |-------------| <-- Baseaddressen for Flash minne *0x0800 0000*

    SRAM (Static Random Access Memory):

    |-------------|
    |             |
    |             |
    |             |
    |-------------|
    | int counter | <-- Midlertidig lagringsplass som brukes for *counter*
    |-------------| <-- Baseaddressen for variablen (ukjent addresse)
    |             |
    |             |
    |-------------| <-- Baseaddressen for SRAM *0x2000 0000* 

4. Maskinkode og assembly instruksjoner etter bygging av koden

| Addresseskyv | Maskinkode | Assembly Instruksjoner | Kommentar |
| --------------- | ------------ | ---------------------------- | ------------------------ |
| 0: (32 bit) | 0xf240 0300 | `movw r3, #:lower16:counter` |`r3 = &counter bit: 15-0` |
| 4: + 4 (32 bit) | 0xf2c0 0300 | `movt r3, #:upper16:counter` |`r3 = &counter bit: 16-31`|
| 8: + 4 (16 bit) | 0x6818 | `ldr r0, [r3, #0]` | `r0 = *r3` |
| a: + 2 (16 bit) | 0x1c42 | `adds r2, r0 #1` | `r2 = r0 + 1` |
| c: + 2 (16 bit) | 0x601a | `str r2, [r3, #0]` | `*r3 = r2` |
| e: + 2 (16 bit) | 0x4740 | `bx lr` | `return r0` |
> **0:, 4:** Fordi addressen til counter er 32 bit så må den deles opp i 2 16-bits addresser i prosessor minnet. Så de 16 første bit-ene ligger i addresse `0xf2c0 0300` mens de 16 siste bit-ene ligger i addresse `0xf240 0300`
> **8:** *Last inn inholdet i cellen som ligger på addressen til r3 + 0*. Denne innstruksjonen henter verdien til counter fra SRAM (r3 er addressen til counter) inn i prosessoren i r0 registeret.
> **a:** *Ta verdien i register r0 og legg adder 1 til verdien. Deretter lagre dette i register r2.*
> **c:** *Lagre verdien i r2 i SRAM (\*r3 = pointeren til minneaddressen til counter)*
> **e:** *hopp tilbake til "kalleren"*


## Instruksjonsett ARM Cortex M3 (assembly instruksjoner)
### Grundig innsikt i instruksjons formatet
Eks:
**0x1c42:** `adds r2, r0, #1`
**#** betyr direkte verdi (immediate).
> Fra **Encoding T1:** `Rd = r2, Rn = r0, imm3 = 1`

> Forklarer hva som for eksempel at det er selve register tallene som skal inn og ikke minneaddressen eller lignende. I tillegg ser vi at vi kun kan *immediate* addere et tall som får plass i max 3 bit aka. 2^3 aka. 0 - 7

> Dette forklarer hvorfor maskinkoden til operasjonen `adds r2, r0, #1` blir **0x1c42:**
#### Flytting
##### Flytting til minne
> Ønsker å lagre r3 i 3 forkjellige registere i SRAM.
> 1. Lagre r3 i r4 i SRAM. R4 er baseaddressen til r4 (0x20005000) + 4 som betyr 4 "hakk" opp fra baseaddressen. Hiver da inn den minst signifikante (bakerste) biten i første område og fortsetter oppover til hele r3 er lagret i SRAM.
> 2. Samme som nr. 1, men vi har `strh` som betyr 2 Byte (16 bit). Vi begynner igjen med de minst signifikante tallene og fyller bare to celler. **Hvis vi ønsker å lagre de to mest signifikante tallene (0xFE og 0xDC) så må vi *høyre-skifte* (`r3>>16`) tallene**.
> 3. Samme som nr. 2 bare at vi bruker `strb` som betyr store byte som er 1 Byte (8 bit) og bare kan lagre i 1 celle og cellen er r4 + 0 så den første cellen.

##### Lasting fra minne
> Hvis man bare skal hente ut 16 bit av 32 bit så vil man bare hente ut de to minst signifikante 16 bit-ene. Resten av bit-ene blir nullstillt

##### Plassering av tallverdi inn i et register når det ikke er plass
Hvis man skal flytte f.eks en addresse inn i et register så er det ofte ikke plass. Man kan kanskje få plass til bare addressen, men fordi det også legges til tilleggsinformasjon som forteller hva denne instruksjonen er så må man bruke:
* `movw`: move wide: Tar den siste delen av addressen
* `movt`: move top
[Eksempel på bruk](###Tabular-oversikt-over-inkrementeringmetode)
[StackOverflow eksempel](https://stackoverflow.com/questions/7800055/movw-and-movt-in-arm-assembly)

#### Hopping
To typer:
* Hopp med vilkår
* Vil sjekke om en "condition" er oppfylt før den hopper
* 
* Alle operasjoner påvirker statusbit i prosessor status registeret
* 
* Disse hopper ved vilkår:
* 
* Hopp uten vilkår
* 
* Lenkeregisteret (LR) holder vare på returaddressen til funksjonen som kalte på den. Hvis man kaller en metode som kaller en metode som kaller en metode ... Så holder det ikke å bare ta vare på en return addresse. Da trenger man en **stack** som *pusher* når en ny funksjon blir kalt og *popper* når man returnerer.
* 
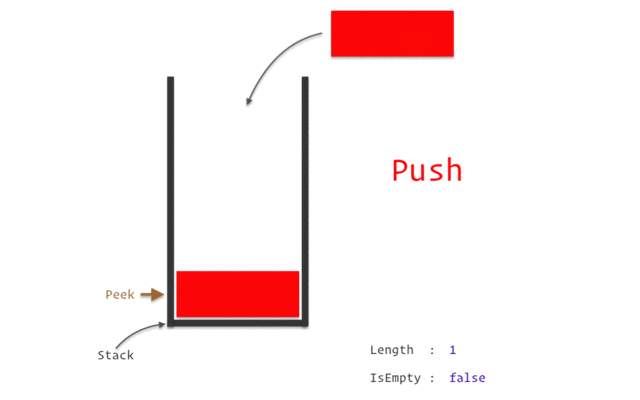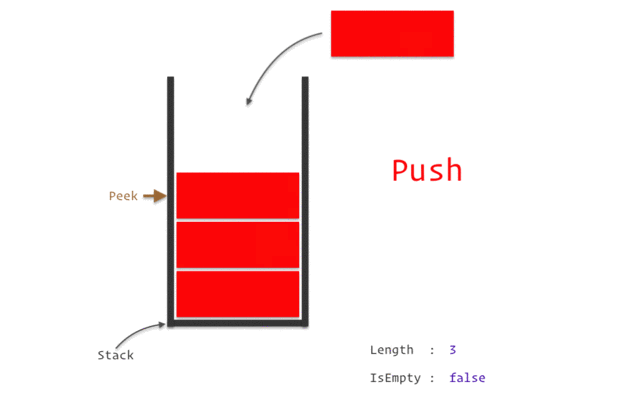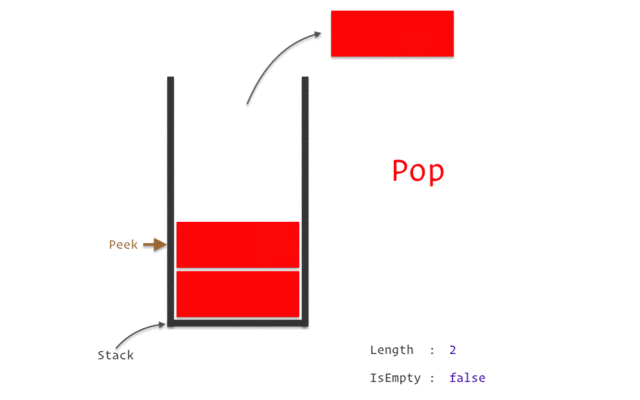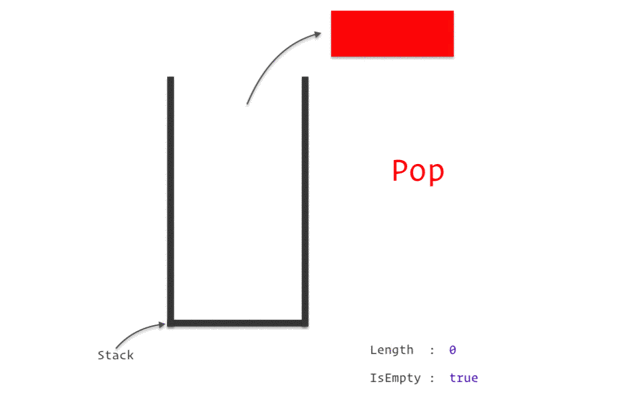
> Eksempel på en **stack**

## Avbrudd

graph LR
    A(Kilde) -->|Sender et avbrudd signal| B(MP)
    B --> |Automatisk oppstart av en handler| C(Handler)

> Viser en kilde som sender et avbruddsignal. Mikroprosessoren fanger dette opp og automatisk går og ser i en *vektor tabell* hvor den ser hvilke handler den skal starte opp.
> Det kan f.eks. være at du vil med 1ms mellomrom hente data fra en bryter for å se om den er trykket inn eller ikke.

### Gang
1. Avbruddsignal blur sendt til mp
2. mp henter startaddressen til hanlere fra en **vektortabell** hvor de ligger.
3. Starter opp handlerene (`PC = &handler // når programmtelleren settes lik baseaddressen til handleren så begynner prosessoren automatisk å starte programmet`)

### Ved avbrudd
1. Kjører ferdig maskininstruksjonen den holder på med
2. Sikkerhetskopierer en **Stakkramme**, som er informasjonen angående hva mp holdt på med akkurat nå, inn på stakken.
3. Setter `PC = &handler`
4. Legger så inn en kode `EXC (exception)`. Denne koden har til hensikt å fortelle mp at den må hente tilbake den **stakkrammen** fra *2.* etter den er ferdig med avbruddet så den kan fortsette hvor den slapp.
5. Kjører handleren
6. Gjenopprett *staten*

### MSR & MRS
Brukes for flytting fra spesialregister til register r0-r15 (MSR) og fra register r0-r15 til spesialregister (MRS)

## Programstruktur
*Er ingen fasit*
> Eksempel på hvordan et program som styrer en alarm kan bli satt opp

### Avbruddshåndtering
> Finnes mange forskjellige handlere til forskjellige typer avbrudd.

> Forskjellige avbrudd har også forskjellig prioritet. Hvis det skjer flere avbrudd samtidig, eller mens et annet avbrudd holder på, vil avbruddet med høyere prioritet ta over. Hvis de har samme prioritet så fortsetter alt som vanlig. Det samme skjer med lavere prioritet.

# Kapittel 3 - Digitalteknikk
## Logikk - Hovedgrupper av digitale signaler
### Kombinatorisk logikk
Hvis det er en kombinasjon av inngangssignalene som er sånn og sånn så reagerer man momentant på utgangssignalet
Eksempel:
**Typisk spesifikasjon:**
* Innganger
* Utganger
* Funksjon

### Sekvensiell logikk
*Forskjellen her er at tilstanden du er i **nå** skal være med på å bestemme hva som skal skje.* F.eks *Sykkellyktsystemet* i lab 3 er et sekvensielt system pga. når man trykker på bryteren så må man vite hva signalet er **nå** som påvirker hva signalet skal **bli**.
**Tilstander:** S1 - Sn

#### Synkron
*Tilstandsendringene går i en fast takt styrt av et klokkesignal. Tiden mellom stegene er altså konstante. Dette er den vanligste typen sekvensiell logikk.*

Her trenger man minne for å lagre forrige tilstand

##### Blinklys eksempel

* $t_{BP} = t_{clk}*2^8=2^n*\frac{1}{f_{clk}}$
* $t_{BI} = \frac{1}{2}*t_{BP} = \frac{1}{2}*2^n*\frac{1}{f_{clk}} = 2^{n-1}*\frac{1}{f_{clk}} = 128ms$

#### Asynkron
*Tilstandsendringene skjer når inngangssignalene endrer seg. Tiden mellom slike endringer eller steg er da generelt varierende.*

## Digitalt hierarki

### Transistorer Felteffekttransistoren (MOSFET)
Før: Var det *Bipolar Junction Transistor*. Disse gikk det hele tiden litt strøm i.

Nå: Er det **MOSFET** *Metall Oxide Semiconductor Field Effect Transistor*
> Hovedtanken med denne typen transistor at med å indusere et magnetisk felt ved **G** (i bilde 2) så vi det dannes en slags *kanal* som leder strømmen mellom V~GS~
> NB: Bruker "doping" som ved laging av solcellepaneler.

### Resistor Transistor Logikk
> Når man har et **lavt** nivå på inngangen så er transistoren stengt og ingen strøm går igjennom den eller motstanden. Da er det null spenningsfall i motstanden og en høy **ut**. `Lavt nivå inn --> Høyt nivå ut`

### CMOS Inverter
> Når $A = 0$ *(ingen spenning)* vil forkjellen i spenning mellom V~CC~ og A føre til at Q1 danner en krets *(spenningen går fra V~CC~ til Y)* og $Y=1$.
> Når $A = 1$ *(spenning)* vil spenningen i A føre til at Q2 danner en krets *(spenningen går fra A til Q2) og $Y=0$ fordi strømmen går til jord.

Youtube video [link](https://www.youtube.com/watch?v=hmpVrjm93n4)

### Spenningsforhold
> Må garantere at 1 og 0 ligger imellom et spenningsområde for at mottakeren skal kunne forstå hva som menes hvis kretsen påvirkes av *støy*. Toleransen varierer fra komponent til komponent. Hvordan den

#### Standard spenningsområde for *Høy*
Mottakeren har en innebygd toleranse (noise margin).

### Effektforbruk

2 typer effektforbruk:
* statisk (veldig lavt i CMOS)
* dynsamisk (skjer ved signalendringer)
* Opplading:
* *Bytte mellom 1 og 0 og motsatt skjer ikke umiddelbart. A1 må "lade opp" A2!*
* $C_T$ - Intern kapasitans
* Hvis $A1 = 0 \Longrightarrow A2 = 1$
* $I_C > 0$
> Fører til en oppladning av C~T~ *(source / push situasjon).* Når C~T~ er "fyllt opp" så switcher A2 fra av til på.
* Hvis $A1 = 1 \Longrightarrow A2 = 0$
* $I_C < 0$
> Fører til en utlading av C~T~ *(sink / pull situasjon).* Når C~T~ er "ladet ut" så switcher A2 fra på til av.

###### Gjennomsnittsstrøm: $\overline{I_{C}} = \frac{1}{T}*C_T*V_{CC}=f*C_T*V_{CC}$
> Viktig formel
###### Gjennomsnittseffekt: $P_D=V_{CC}*I_C=f*C_T*V_{CC}^2$
>Forsyningsspenningen teller mye på effektforbruket i en krets

### Ladeintervall for mobiltelefon
###### Kapasitet: $K_B=I_B*T_B$
> Formel for kapasitet i et batteri

Gitt: $C_T=1\mu F,\ \overline{V_{CC}}=2.5V,\ f=100kHz$
1. Hvor mye kapasitet har batteriet?
$K_B = 2000mAh = 2A*3600s\ (1h = 60*60s = 3600s)$
2. Hvor mye energi har batteriet?
$E_B=V_B*K_B \approx 26kJ$
3. Hva er effektforbruket i mobilen?
$P_D=V_{CC}*I_C=f*C_T*V_{CC}^2 =100kHz*1\mu F*2.5V = 0.63W$
4. Hva er ladeintervallet gitt av?
$P_D*T_I=E_B \Longrightarrow T_I=41600s \approx 12t$

## Logiske porter

### Logiske operatorer
#### Funksjonstabellen for de forskjellige logiske operatorene

### Inverter (N) 

* Når $A = 0$ *(ingen spenning)* vil forkjellen i spenning mellom V~CC~ og A føre til at Q1 danner en krets *(spenningen går fra V~CC~ til Y)* som gjør at $Y=1$.
* Når $A = 1$ *(spenning)* vil spenningen i A føre til at Q2 danner en krets *(spenningen går fra A til Q2)* som gjør at $Y=0$ fordi strømmen går til jord.

### Buffer 

Er 2 **invertere** etter hverandre. Virker meningsløst, men målet er å *fordele* signalet ut på flere komponenter. Hvis signalet har for høy strøm så kan buffring fordele signalet fra 1 komponent og ut på flere komponenter.

### *Tristate*-buffer 

* Når $S=0$ $\Longrightarrow Q4 = 0\ \ \& \ \ Q3 = 0$ $\Longrightarrow Y\ er\ frakoblet\ A\ (flytende)$  brukt bl.a. for å koble vekk *ikke brukte* ting fra databussen.

### NOG (NAND) 

###### Forklaring:

**A** og **B** blokkerer jord. <br /> Altså begge må være på for at Y skal slås av. <br /> Hvis $A \| B = 0 \Longrightarrow Q2 \| Q4 = av\ (lukket)$. <br /> Hvis begge er 1 vil strømmen gå til jord <br /> istedenfor til Y.


### OG (AND) 

###### Forklaring:
Samme som **NOG-port**, men signalet sendes <br /> til en **inverter** og snus.


### NELLER (NOR) 


###### Forklaring:

### ELLER (OR) 

###### Forklaring:

### XNELLER (XNOR) 

###### Forklaring:

### XELLER (XOR) 
> Den øverste varianten bruker 22 transistorer, mens den nederste bare bruker 16.

###### Forklaring:
Realiserer en XELLER (XOR) funksjon ved bruk av en kombinasjon av andre funksjoner. Det finnes to enkle varianter.

## Tidsforsinkelser
Det vil alltid være små forsinkelser når man i switchingen i kretsene. Når man går fra *på* til *av* eller motsatt så må kondensatoren *lades opp* eller *lades ut* først. Dette skjer ganske fort, men med flere logiske porter etter hverandre så *adder* der opp. I tillegg så kan kan det være lettere å *lade ut* en kondensator enn å *lade den opp* eller motsatt.

I programerbar elektronikk så kan mange av disse portene komme etter hverandre fordi det er **mindre kapasitans** og **miniatyrisert** som fører til **mindre effektforbruk**.

Hvor fort stort *delay* det er mellom switchingen påvirker også hvor høy klokkefrekvens det er mulig å ha igjennom kretsen.


###### Eks

## Boolsk Algebra

### De Morgan
**3.18**
| $A$ | $B$ | $\overline{A}$ | $\overline{B}$ | $A*B$ | $\overline{A*B}$ | $\overline{A}+\overline{B}$ |
| --- | --- | -------------- | -------------- | ----- | ---------------- | --------------------------- |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 |

**3.19**
| $A$ | $B$ | $\overline{A}$ | $\overline{B}$ | $A+B$ | $\overline{A+B}$ | $\overline{A}*\overline{B}$ |
| --- | --- | -------------- | -------------- | ----- | ---------------- | --------------------------- |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 |

##### Eksempel på forenkling
$Y=(\overline{AB)+(AC)}+\overline{A}\overline{B}\overline{C}\\=(\overline{A}+\overline{B})(\overline{A}+\overline{C})+\overline{A}\overline{B}\overline{C}\\=\overline{A}\overline{A}+\overline{A}\overline{C}+\overline{B}\overline{A}+\overline{A}\overline{B}\overline{C}\\=\overline{A}+\overline{A}\overline{C}+\overline{B}\overline{A}+\overline{B}\overline{C}+\overline{A}\overline{B}\overline{C}\\=\overline{A}(1+\overline{C})+\overline{A}\overline{B}(1+\overline{C})+\overline{B}\overline{C}\\=\overline{A}+\overline{A}\overline{B}+\overline{B}\overline{C}\\=\overline{A}(1+\overline{B})+\overline{B}\overline{C}\\=\overline{A}+\overline{B}\overline{C}$

### Fra Funksjonstabell til Logisk Likning (SOP-metoden)
**Gitt funksjonstabell**

|A|B|Y|
|-|-|-|
|0|0|0|
|0|1|1|
|1|0|1|
|1|1|1|
>
$Y = \overline{A}*B+A*\overline{B}+A*B$
> Dette er alle kombinasjoner som gir at Y = 1

**Dette kan forenkles**
$Y=\overline{A}*B+A(\overline{B}*B=\overline{A}B+A$
> **3.15** sier at $X\overline{Y}+\overline{X}=\overline{Y}+\overline{X}$
> $X = \overline{A}$ og $\overline{Y} = B$

$Y = \overline{Y}+\overline{X}=B+\overline{A}=A+B \Longrightarrow$ **Eller-operasjon**

## FPGA
### LUT
* Dekoder
* Minne
* Buffer

* Poenget er at med rett innhold i minnecellene så oppfører LUT-en seg som en XOR.
* Å programmere en FPGA, er å følge SRAM-en i LUT-ene med rette verdier
* 

### Multiplekser
> `3 --> 8 MUX`
> Dette eksempelet har 3 inngangssignaler (2^3^ kombinasjoner). Dette gjør at du kan velge å slippe igjennom 1/8 signaler.

#### Realisering av `1 --> 2 MUX`
1. Spesifikasjon vhja. blokkskjema
> En `/` over en linje betyr at *bitbredden* på kanalen er lik størrelsen på tallet som hører til.
2. Funksjonstabell
|S|Y|
|-|-|
|0|A|
|1|B|
3. SOP-basert logisk likning
$Y = \overline{S}*A+S*B$
4. Logisk skjema

### MUX-IC
> Eksempel: `74HC151 = (8 --> 1 MUX)`

> * **S~0~ - S~2~** *Seleksjon av 1 av 2^3^ signal*
> * **I~0~ - I~7~** *Innsignal*
> * **$\overline{E}$ (Enable)** *Åpning **($\overline{E}$ = 0)** eller stenging **($\overline{E}$ = 1)** av kretsen*
> * Kalles et *aktivt lavt signal*.
> * Det er raskere å slå av et signal enn å starte det.
> * 

### Tidsdiagram
Bruker eksempelet [Realisering av `1 --> 2 MUX`](#Realisering-av-`1--->-2-MUX`)
1. | A | B | $\overline{A}$ | Y |
| --- | --- | -------------- | --- |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 |
2. $Y=\overline{A}*B$
3. 
> $tp_1 = ?$
> $tp_2 = 2*tp_1$
4. 
> *`Y_i` er Y~ideell~*

### Dekoder

#### 2 --> 4 Dekoder
1. 
2. | S~1~ | S~0~ | Y~3~ | Y~2~ | Y~1~ | Y~0~ |
| ---- | ---- | ---- | ---- | ---- | ---- |
| 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 |
3.
* $Y_0=\overline{S1}*\overline{S0}$
* $Y_1=\overline{S1}*S0$
* $Y_2=S1*\overline{S0}$
* $Y_3=S1* S0$
4. 

### Digital Komparator
> Sammenlikner to verdier. F.eks `A > B`.

#### Realiseres på 2 ulik måter
1. Vhja. dedikert logikk
* Siffervis m/start i A~0~, B~0~ (lsb)
* | A~0~ | B~0~ | Q~0,a>B~ | Q~0,a=B~ | Q~0,a<B~ |
| ---- | ---- | -------- | -------- | -------- |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 |
* 

2. Basert på subtraksjon i ALU (trenger en prosessor)

### Adderer
> Trenger mente hvis man overgår 32-bits formatet

Funksjonstabell:
| A~0~ | B~0~ | S~0~ | C~1~ |
| ---- | ---- | ---- | ---- |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| | | XOR | AND |

> HA = Halv-adderer
> FA = Full-adderer

Er et problem fordi den neste addereren må vente på mente fra den forrige. Har derfor utviklet en *carry-lookahead* metode som predikerer mente.

## Sekvensiell logikk

To typer:
* Asynkron:
* Endringen skjer når inngangssignalet endrer seg
* 

* Synkron:
* Skjer ved klokke tikk
* 

### Minneelement for sekvensiell logikk
*Hovedforskjellen mellom dem er at ei **vippe** kan bare endre tilstand ved faste tidspunkt styrt av ei klokke. En **lås** kan endre tilstand når det skjer endringer på inngangen.*

### NELLER S/R lås
> Denne baserer seg på NELLER porter

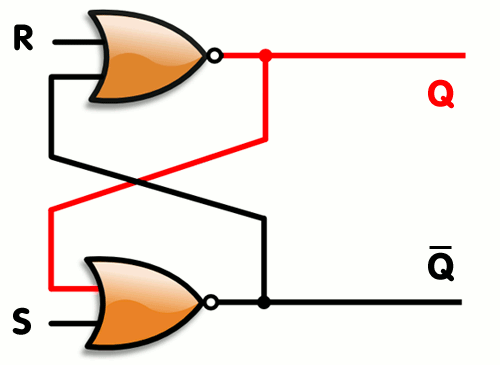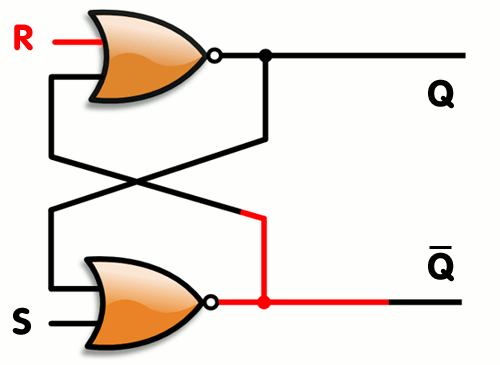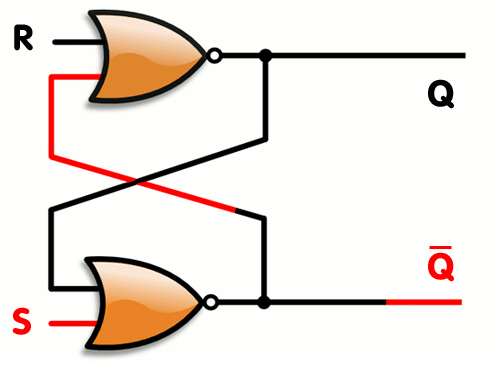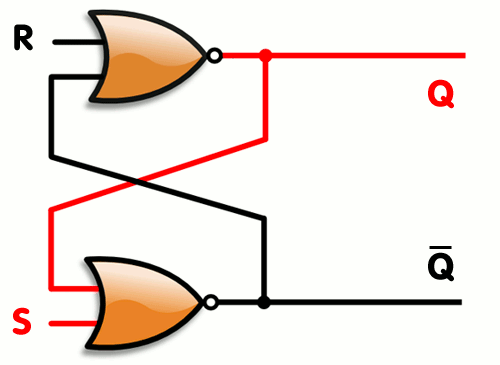
> Animasjonen er oppned!

**Når R er satt så vil en ny R-puls ikke gjøre noen endringer i signalet. Den er da låst!**

### NOG S/R lås
> Denne baserer seg på NOG porter

### 3 metoder for avprelling
1. RC-filter
2. Digitalt filter
* Skiftregister
* SR lås (spesiell utgave med 3 kontaktpunkt)
* 
3. Programmvare
* Sampler p åbestemte intervaller og trenger da f.eks 3 etterfølgende like verdier for å godkjenne trykk eller slepp.

### Race condition
> Hvis xS og xR blir 1 samtidig så vil vi ende opp i en *reset situasjon*. xS er den raskeste og blir da *straffet* for det fordi den ender opp med å bli 0.
**Den tregeste bestemmer tilstanden**. Vanligvis er etterslep ukjent så vi kan ikke forutsi hva som er den *raskeste*. For å unngå *race condition* må man legge på en **datalås**.

### Datalås
> Inngangssignaleene vil her *nesten* alltid være ulike.
> 
> Det er et lite delay fra når inverteren *inverterer* signalet at begge vil være like og kan derfor fremdeles påvirkes av *glitch*-er.

#### Transparent Datalås 
> Har et ekstra *Enable* **E** signal som brykes til å åpne og lukke låsen.
> * E = 1: Låsen er åpen - verdien endrer seg når D endrer seg.
> * E = 0: Låsen er stengt - vil lagra den verdien som D hadde rett før stenging.

### Datavippe 
Det er ikke altid bare nok å ha et stengt/åpent signal (E). I mange system vil man at endringene bare skal skje på bestemte tidspunkt. Altså at ting også påvirkes av klokkesignalet.
>