---
tags: Data Structure
---

# Final 考試重點

# Chapter 05

## 1. Binary search tree
> - Definition
> - Iterative search program
> - Each value being inserted into/ deleted from the tree
> - ppt. p.51-58.
> - Textbook: Sect. 5.7.3 Fig. 5.30, p.234

### Binary search tree definition

- Every element has a **unique key**.
- The keys in a nonempty **left subtree** (**right subtree**) are **smaller** (**larger**) than the key in the root of subtree.
- The left and right **subtrees** are also binary search trees.

### Recursive search program

tree_pointer search(tree_pointer tree, int key) {
    // return a pointer to the node that contains key.
    // If there is no such node, return NULL.
    if (!root)
        return NULL;
    if (key == root->data)
        return root;
    if (key < root->data)
        return search(root->left_child, key);
    return search(root->right_child, key);
}

### Iterative search program

tree_pointer search2(tree_pointer tree, int key) {
    // return a pointer to the node that contains key.
    // If there is no such node, return NULL.
    while (tree) {
        if (key == tree->data)
            return tree;
        if (key < tree->data)
            tree = tree->left_child;
        else
            tree = tree->right_child;
    }
    return NULL;
}

### Inserted into the binary tree

void insert_node(tree_pointer *node, int num) {
    // If num is in the tree pointer at by node, do nothing;
    // otherwise add a new node with data = num.
    
    /* modified_search is modified from iterSearch which
     * return NULL if the tree is empty or if num is presented.
     * Otherwise it returns a pointer to the last node of
     * the tree that was encountered during the search.
     */
    tree_pointer ptr, temp = modified_search(*node, num);
    if (temp || !(*node)) {
        // num is not in the tree
        ptr = (tree_pointer) malloc(sizeof(node));
        if (IS_FULL(ptr)) {
            fprintf(stderr, "The memory is full\n");
            exit(1);
        }
        ptr->data = num;
        ptr->left_child = ptr->right_child = NULL;
        if (*node) {
            // insert as child of temp
            if (num < temp->data)
                temp->left_child = ptr;
            else
                temp->right_child = ptr;
        } else {
            *node = ptr;
        }
    }
}

### Deletion from the binary tree

Three conditions should be considered:

1. **Leaf** -> delete directly.
2. **Has one child** -> delete and change the pointer to this child.
3. **Has two child** -> either the smallest element in the right subtree or the largest element in the left subtree.
- **從左子樹找最大或從右子樹找最小的節點** （假設為 x），x 必為 case 1 或 case 2，用 x 的值取代原本要刪除的節點後，再將 x 節點刪除。
- [詳細說明](http://alrightchiu.github.io/SecondRound/binary-search-tree-sortpai-xu-deleteshan-chu-zi-liao.html#delete)

### Binary search tree time complexity

- **Searching, insertion, removal**
- $O(h)$, where $h$ is the **height** of the tree.
- Worst case - **skwed （歪斜） binary tree**.
- $O(n)$, where $n$ is the **number** of internal nodes.

# Chapter 06
## 1. Graph definition and representation

> - ppt. 1-20
> - Textbook: Section 6.1.2-6.1.3.2

- [Definition](https://hackmd.io/W3pU80U1TY6od32-ibdVJg#The-graph-ADT)
- [Representation](https://hackmd.io/W3pU80U1TY6od32-ibdVJg#Graph-representations)

## 2. Graph DFS and time complexity for different data structure

> - ppt. 29-33
> - Textbook: Section 6.2.1-6.2.2

- DFS : Preorder traversal

### DFS implementation

#define MAX_VERTICES 50 // maximum number of vertices
typedef struct node *node_pointer;
typedef struct node {
    int vertex;
    struct node *link;
};
node_pointer graph[MAX_VERTICES];
int n = 0; // vertices currently in use

#define FALSE 0
#define TRUE 1

short int visited[MAX_VERTIES];

void dfs(int v) {
    // depth first search of a graph begin node_pointer w
    
    node_pointer w;
    visited[v] = TRUE;
    printf("%5d", v);
    for (w = graph[v]; w; w = w->link) {
        if (!visited[w->vertex]) dfs(w->vertex);
    }
}

### DFS time complexity for different data structure

- Adjacency list: $O(e)$
- $e = \cfrac{n(n-1)}{2}$ is number of edges.
- Adjacency matrix: $O(n^2)$

## 3. Graph BFS and time complexity for different data structure

> - ppt. 29-33
> - Textbook: Section 6.2.1-6.2.2

- BFS : level order traversal

### BFS implementation

#define FALSE 0
#define TRUE 1

short int visited[MAX_VERTIES];

void bfs(int v) {
    node_pointer w;
    queue_pointer front, rear;
    front = rear = NULL; // initialize queue

    printf("%5d", v);
    visited[v] = TRUE;
    addq(&front, &rear, v);
    while (front) {
        v = deleteq(&front);
        for (w = graph[v]; w; w = w->link) {
            if (!visited[w->vertex]) {
                printf("%5d", w->vertex);
                addq(&front, &rear, w->vertex);
                visited[w->vertex] = TRUE;
            }
        }
    }
}

### BFS time complexity for different data structure

- Adjacency list: $O(e)$
- Adjacency matrix: $O(n^2)$

## 4. Three minimum cost spanning trees algorithms + cost of the spanning tree

[三種演算法](https://z1nhouse.github.io/post/p0rM7JmKv/)

> - Kruskal’s, Prim’s, Sollin’s algorithms
> - Cost of the spanning tree
> - ppt. 49-55
> - Textbook: Section 6.3.1-6.3.3.

[spanning tree](https://mycollegenotebook.medium.com/%E7%94%9F%E6%88%90%E6%A8%B9-spanning-tree-fa19df652efb)

- The cost of a spanning tree of a weighted, undirected graph is the **sum of the costs** (weights) of the **edges in the spanning tree**.
- Minimum cost spanning tree must satisfy:
- Use **only edges** within the graph.
- Use **exactly** $n - 1$ edges.
- Not use edges that produce a cycle.

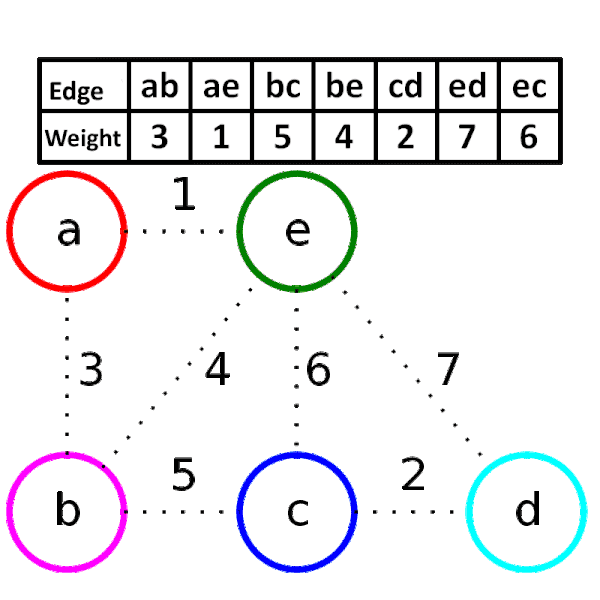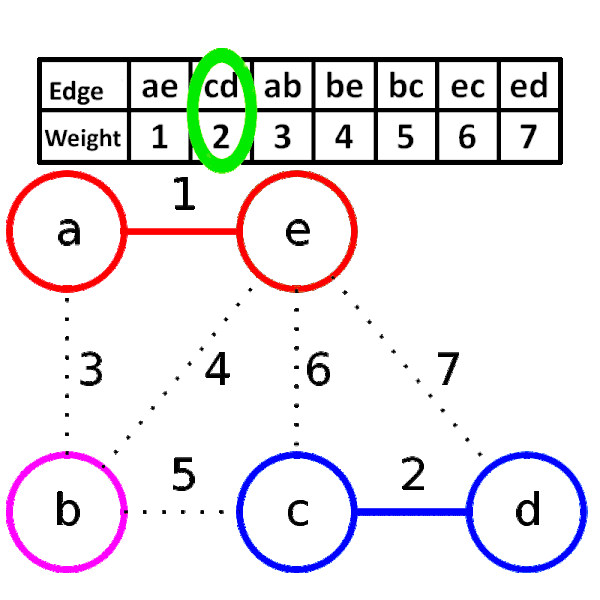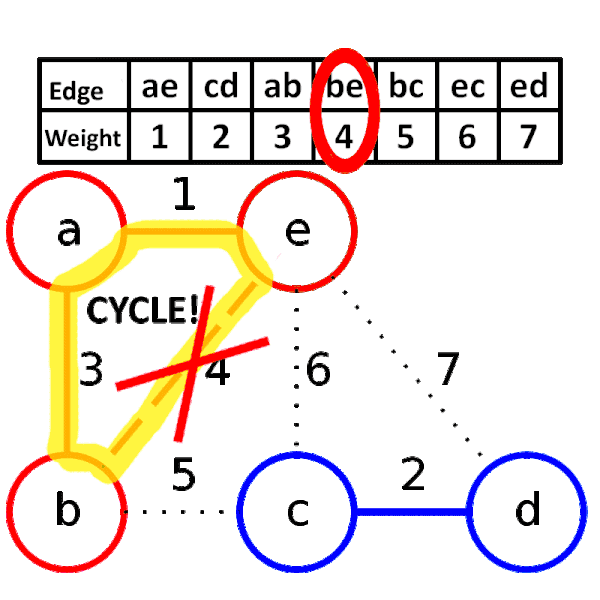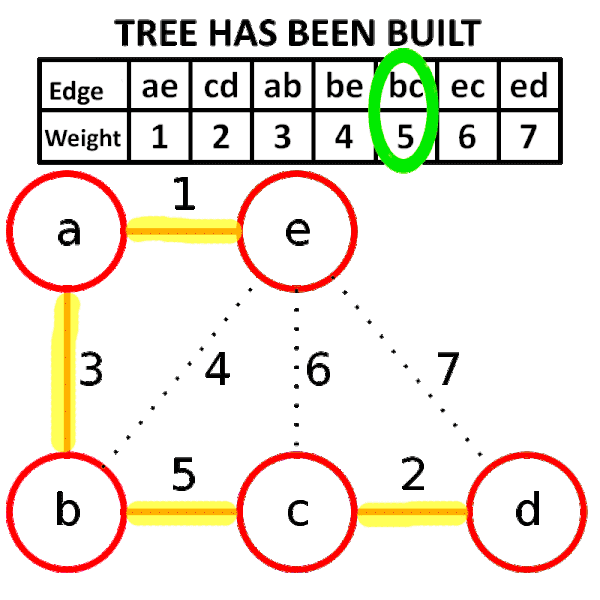
### [Kruskal’s Algorithm](https://mycollegenotebook.medium.com/kruskal-algorithm-deb0d64ce271)

1. Build a minimum cost spanning tree $T$ by **adding edges to $T$ once at a time**.
2. Select the edges for inclusion （包含） in $T$ in **non-decreasing order of the cost**.
3. An edge is added to $T$ if it does **not form a cycle**.
4. Since $G$ is connected and has $n > 0$ vertices, **exactly $n - 1$ edges** will be selected.

- **Time complexity: $O(e \log e)$**

Pseudocode:

T = {};
while (T contains less than n - 1 edges && E is not empty) {
    choose a least cost edge (v, w) from E;
    delete (v, w) from E;
    if ((v, w) does not create a cycle in T)
        add (v, w) to T;
    else
        discard (v, w);
}
if (T contains fewer than n - 1 edges)
    printf("No spanning tree\n");


### [Prim’s Algorithm](https://ithelp.ithome.com.tw/articles/10205823)

1. Build a minimum cost spanning tree $T$ by **adding edges to $T$ once at a time**.
2. At each stage, add a **least cost edge** to $T$ such that the **set of selected edges is still a tree**.
3. Reapeat the edge addition until $T$ contains $n - 1$ **edges**.

Pseudocode:

T = {};
TV = {0};    // start with vertex 0 and no edges
while (T contains fewer than n - 1 edges) {
    let (u, v) be a least cost edge such that u in TV and v not in TV;
    if (there is no such edge)
        break;
    add v to TV;
    add (u, v) to T;
}
if (T contains fewer than n - 1 edges)
    printf("No spanning tree\n");


### [Sollin’s Algorithm](https://garychang.gitbook.io/data-structure/4-graph/4.3-spanning-tree/4.3.3-sollins-algorithm)

1. Select **several edges** for inclusion in $T$ at each stage.
2. At the start of a stage, the selected edges forms a **spanning forest**.
3. During a stage we **select a minimum cost edge** that has **exactly one vertex** in the tree edge for each tree in the forest.
4. Repeat until only tree at the end of a stage or no edges remain for selection.

# Chapter 07

## 1. 5 different sorting algorithms. At least 2-3 problems with partial codes or sorting process as problems from homework

> - At least 2-3 problems with partial codes or sorting process as problems from homework (e.g. exercise 1, p.355)

[Chapter7 - Sorting](/PJW-SRN5QtGBIHXyfbw1Yw)