## 段考剛結束
#### 我們來休息一下
#### 來做一些比教輕鬆的事
----
能先幫我們填一下表單嗎
[press this](https://forms.gle/nb376SuwB6QkRAFDA)
放心 不是rickroll
https://forms.gle/nb376SuwB6QkRAFDA
----
但教學們很扣黏 :cry:
段考完當天晚上就要來做教學簡報
----
段考完 我先不教新東西
今天主要來解題 :+1:
---
#### 接下來來復習一下上次教的
~~大家還記得嗎~~
----
#### 我們教了Def
(你可以定義一個任何你想要的函數)
----
### def的用法
```
公式:
def 名字(你要帶入的參數):
程式碼
```
----
這樣大家都記起來了嗎?
----
補充一下上次有人問的
print(f " ")
print 中為什麼要加f
----
```
在Python中,加入 f 前綴是為了使用「格式化字符串
這被稱為「格式化字符串字面值」(formatted string literal)
在這樣的字符串中,你可以透過在字符串中嵌入表達式,引用變數或執行其他Python代碼。
```
----
舉例
```py!
name = "John"
age = 25
# 使用 f-string 進行字符串格式化
print(f"My name is {name} and I am {age} years old.")
```
----
說明
```
在這個例子中,f"My name is {name} and I am {age} years old."
就是使用 f-string 格式化的字符串
在字符串中的花括号 {} 內部,你可以放置變數、表達式等
這些在運行時會被替換為實際的值。
在 print(f" ") 中,f 前綴表示字符串中可能包含表達式
而 {} 內部的內容將被替換為相應的值
這使得字符串的構建更直觀和方便。
```
---
#### 那我們先來完成上次還教完的那幾題
----
#### 題目2:編寫一個函數,找出兩個數字的最大公因數(GCD)。
----
我這裡先提一下
python中有一種用法能讓進位制前後位移一個位數
```py!
>>
<<
```
有點亂 對吧
我詳細解釋一下
----
當涉及到位運算時,我們首先要了解數字在計算機內部是如何表示的。計算機使用二進制來表示整數。在二進位中,每一位可以是 0 或 1。一個二進位位元稱為一個位元。
----
例如,整數 8 在二進位中表示為 001000。這個二進制數有四位,分別是 1、0、0、0。
----
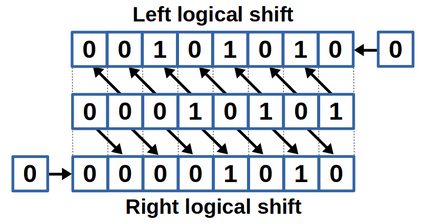
現在,讓我們來看看右移運算子 >> 的作用。右移運算子將二進制數向右移動指定的位數,丟棄右側多餘的位,並在左側用零填充。右移一位相當於除以 2,右移兩位相當於除以 4,以此類推。
----
同理<<
----

----

----
舉例
```py!
x = 8 # 二進位表示為 001000
y = x >> 2 # 右移兩位,結果為 000010,即十進位的 2
```
----
第二個補充
```py!
&
```
那麼這是什麼呢
----
```
在Python中,& 是位元與操作符。
它用來執行兩個整數之間的位元與操作,對於每一對對應的位
只有在兩個操作數的對應位都是1時,結果的對應位才為1。
```
----
```py!
a = 5 # 0b0101
b = 3 # 0b0011
result = a & b
print(result)
# 輸出1,因為只有在最低位元時兩者都是1
```
在這個例子中,a 和b 的二進位表示中,只有最低位元同時為1,所以結果是1。
----
大家都了解後
再來解看看吧
----
解法
```py!
def gcd(a, b):
if a == b:
return a
if a == 0:
return b
if b == 0:
return a
if a & 1 == 0: # 如果a是偶数
if b & 1 == 1: # 如果b是奇数
return gcd(a >> 1, b)
else:
return gcd(a >> 1, b >> 1) << 1
if b & 1 == 0: # 如果b是偶数
return gcd(a, b >> 1)
if a > b:
return gcd((a - b) >> 1, b)
return gcd((b - a) >> 1, a)
```
```
a = 56
b = 48
result = gcd(a, b)
print(f"{a} 和 {b} 的最大公約數為 {result}")
```
----
是的
程式很長X_X
容我慢慢解釋
----
### 首先
這裡定義了一個函數 gcd,它接受兩個參數 a 和 b。首先,檢查了一些特殊情況,如果 a 和 b 相等,那麼它們本身就是最大公約數。如果其中一個為零,那麼另一個就是最大公約數。
```py!
def gcd(a, b):
if a == b:
return a
if a == 0:
return b
if b == 0:
return a
```
----
那這幾行呢
```py!
if a & 1 == 0: # 若a是偶數
if b & 1 == 1: # 如果b是奇數
return gcd(a >> 1, b)
else:
return gcd(a >> 1, b >> 1) << 1
```
----
接下來,程式檢查 a 是否為偶數。如果是偶數,它進一步檢查 b 是否為奇數。
如果 b 是奇數,那麼兩者的最大公約數仍然是 a 和 b 之間的最大公約數。
如果 b 也是偶數,它將遞歸地計算 a >> 1 和 b >> 1(即右移一位,相當於除以 2),然後將結果左移一位(相當於乘以 2)。這是因為兩個偶數的最大公約數的 2 倍,仍然是它們的最大公約數。
----
如果 a 是奇數而 b 是偶數,那麼程式將遞歸地計算 a 和 b >> 1 的最大公約數。這是因為偶數和奇數的最大公約數仍然是奇數。
```py!
if b & 1 == 0: # 如果b是偶數
return gcd(a, b >> 1)
```
----
最後,如果 a 和 b 都是奇數
程式將遞歸地計算 a 與 (a - b) >> 1 或 b 與 (b - a) >> 1 的最大公約數,取決於哪一個數較大。
這是透過減去較小的數,然後右移一位來實現的,以確保遞歸過程中使用的數是奇數。
最終,透過這樣的遞歸過程,找到了 a 和 b 的最大公約數,並將其傳回。
```py!
if a > b:
return gcd((a - b) >> 1, b)
return gcd((b - a) >> 1, a)
```
----
最後,程式使用給定的兩個數來呼叫 gcd 函數,並將結果列印出來。在這個例子中,輸入為 a = 56 和 b = 48,輸出將是這兩個數的最大公約數。
```py!
a = 56
b = 48
result = gcd(a, b)
print(f"{a} 和 {b} 的最大公約數為 {result}")
```
----
好吧
我沒想到這題要說明19頁X_X
---
#### 題目: 撰寫一個函數,接受一個正整數 n,回傳斐波那契數列的第 n 項。
那麼什麼是費氏數列呢
----
```
費氏數列(Fibonacci sequence)是一個數學上的數列
起始於0和1,之後的每一個數字都是前兩個數字的和。
第三個數字是前兩個數字的和,第四個數字是前兩個數字的和,依此類推。
```
```
舉個例子
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...
```
----
解答
```python
def fibonacci(n):
a, b = 0, 1
for _ in range(n - 1):
a, b = b, a + b
return a
# 測試
print(fibonacci(7)) # 13
print(fibonacci(10)) # 55
```
----
說明
```
a 和 b 是兩個變數,用來追踪費氏數列中的兩個相鄰的數字。
for _ in range(n - 1): 是一個迴圈,迭代n-1次。
這是因為我們已經初始化了a和b的值,所以我們只需要再迭代n-1次,就能得到第n項的值。
a, b = b, a + b 是一個同時賦值的操作
這樣可以在不使用臨時變數的情況下交換a和b的值,同時計算下一個數字。
最後,函數返回變數a的值,這是費氏數列的第n項。
```
---
下一題
#### 題目:編寫一個函數,找出一個數字的所有因數。
----
```py!
def find_factors(number):
factors = []
for i in range(1, number + 1):
if number % i == 0:
factors.append(i)
return factors
```
----
```
def find_factors(number)::這一行定義了一個函數 find_factors,它有一個參數 number,表示要找因子的整數。
factors = []:建立一個空列表 factors,用於儲存找到的因子。
for i in range(1, number + 1)::這是一個循環,從 1 循環到 number,包括 number。 range(1, number + 1) 產生一個從 1 到 number 的範圍。
if number % i == 0::這一行檢查 i 是否為 number 的因子,即是否能夠整除。如果是因子,就執行下面的語句。
factors.append(i):將找到的因子 i 加入 factors 清單中。
```
----
```
最終,return factors 將包含所有因子的清單傳回給呼叫者。
舉例說明,如果你呼叫 find_factors(12),這個函數會回傳 [1, 2, 3, 4, 6, 12]
因為 12 的因數是 1、2、3、4、6 和 12。
```
---
#### 題目:編寫一個函數,找出一個數字是否為質數。
----
我覺得這里需要補充一下
a的0.5次方=根號a
(這個部分你們可能學過也可能幾個月後就會學)
----
```py!
def is_prime(number):
if number <= 1:
return False
for i in range(2, int(number**0.5) + 1):
if number % i == 0:
return False
return True
```
----
```python
def is_prime(number):
if number <= 1:
return False
```
說明
```
def is_prime(number)::這一行定義了一個函數 is_prime
它有一個參數 number
表示要檢查是否為質數的整數。
if number <= 1::這一行檢查 number 是否小於或等於 1
如果是,那麼根據質數的定義,它不是素數,因為質數是大於 1 的正整數
因此,函數傳回 False。
```
----
```python
for i in range(2, int(number**0.5) + 1):
if number % i == 0:
return False
```
說明
```
for i in range(2, int(number**0.5) + 1)::這是一個循環
從 2 循環到 number 的平方根(包括平方根)
這是因為如果一個數不是質數
它必定有一個因子在平方根以下。
if number % i == 0::在循環中,檢查 number 是否能夠被 i 整除,即是否有因數
如果有因子,那麼 number 不是質數,因此函數傳回 False。
```
----
```python
return True
```
說明
```
如果經過循環,沒有找到能整除 number 的因子,那麼 number 是質數,函數傳回 True。
綜合起來,這個函數的作用是判斷給定的整數是否為質數。如果是質數,傳回 True,否則傳回 False。
```
---
#### 題目:編寫一個函數,計算於一個範圍內所有質數的總和。
----
```py!
def sum_of_primes_in_range(start, end):
total = 0
for num in range(start, end + 1):
if is_prime(num):
total += num # 使用之前定義的is_prime函數
return total
```
----
```python
def sum_of_primes_in_range(start, end):
total = 0
```
說明
```
def sum_of_primes_in_range(start, end)::這一行定義了一個函數 sum_of_primes_in_range
它有兩個參數 start 和 end,表示整數範圍的起始和結束。
total = 0:建立一個變數 total,用來累積質數的和。
```
----
```python
for num in range(start, end + 1):
if is_prime(num):
total += num # 使用先前定義的is_prime函數
```
說明
```
for num in range(start, end + 1)::這是一個循環,遍歷從 start 到 end 的整數範圍(包括 start 和 end)。
if is_prime(num)::在迴圈中,檢查目前的 num 是否是質數
這是透過呼叫之前定義的 is_prime 函數來實現的。
total += num:如果 num 是質數,將它加到 total 中。
```
----
```python
return total
```
說明
```
return total:最後,函數傳回累積的質數和作為結果
綜合起來,這個函數的作用是計算給定範圍 [start, end] 內所有質數的和
它透過遍歷範圍內的每個數字,並使用先前定義的 is_prime 函數來檢查每個數字是否為素數
然後將素數累積到 total 變數中,並最終傳回總和。
```
---
#### 題目:撰寫一個函數,接受一個正整數,回傳其數字反轉後的結果。
----
解答
```python
def reverse_number(n):
reversed_n = 0
while n > 0:
reversed_n = reversed_n * 10 + n % 10
n //= 10
return reversed_n
# 測試
print(reverse_number(12345)) # 54321
print(reverse_number(789)) # 987
```
----
說明
```
reversed_n = 0 是用來保存反轉後的數字的變數,一開始初始化為0。
while n > 0: 是一個循環,只要輸入的數字 n 還大於0,就執行循環內的代碼。
reversed_n = reversed_n * 10 + n % 10 將 reversed_n 左移一位(乘以10)
然後加上 n 的個位數(n % 10),這樣就實現了反轉的操作。
n //= 10 是將 n 除以10,去掉已經處理過的個位數。
循環結束的條件是當 n 變為0,表示所有位數都已經處理完畢。
函數返回 reversed_n,這是反轉後的整數。
```
---
#### 題目:撰寫一個函數,接受一個整數列表,回傳所有偶數的平方。
----
解答
```python
def square_of_even(numbers):
return [x**2 for x in numbers if x % 2 == 0]
# 測試
print(square_of_even([1, 2, 3, 4, 5, 6])) # [4, 16, 36]
print(square_of_even([2, 4, 6, 8, 10])) # [4, 16, 36, 64, 100]
```
----
說明
```
for x in numbers 是一個迭代給定的數字列表 numbers 中的每個元素。
if x % 2 == 0 是一個條件判斷,檢查元素 x 是否為偶數。如果是偶數,則進入下一步
如果不是偶數,則跳過該元素。
x**2 計算偶數 x 的平方。
利用列表解析的方式,將每個符合條件的偶數的平方收集起來形成一個新的列表。
函數返回這個新的列表。
```
---
#### 題目:撰寫一個函數,接受一個字串,回傳該字串中所有大寫字母的個數。
----
那麼我們要如何找到大寫字母呢
這時候就要用到一個酷東西
```py!
.isupper
```
----
isupper() 是字符串物件的一個方法
用於檢查字串中的所有字母是否都是大寫字母。
如果字串中的所有字母都是大寫
該方法會返回 True,否則返回 False。
----
例
```py!
text = "HELLO"
result = text.isupper()
print(result) # 輸出 True,因為所有字母都是大寫
```
----
如果字串中至少有一個小寫字母,那麼 text.isupper() 將返回 False。
----
解答
```python=
def count_uppercase_chars(s):
return sum(1 for char in s if char.isupper())
# 測試
print(count_uppercase_chars("Hello World")) # 2
print(count_uppercase_chars("Python")) # 1
```
----
說明
```
for char in s 是一個迭代字符串 s 中的每個字符。
if char.isupper() 是一個條件判斷,檢查字符 char 是否為大寫字母。
如果是大寫字母,則進入下一步;如果不是大寫字母,則跳過該字符。
1 for char in s if char.isupper() 使用了列表解析,對每個符合條件的大寫字母都返回1
最後組成一個由1組成的列表。
sum(...) 計算這個列表中所有元素的和,這樣就得到了大寫字母的數量。
函數返回大寫字母的數量。
```
---
#### 題目:撰寫一個函數,接受一個整數列表,找出其中的最大值。
----
解答
```py!
def find_max_value(numbers):
max_value = float('-inf')
for num in numbers:
if num > max_value:
max_value = num
return max_value
# 測試
print(find_max_value([3, 7, 1, 10, 5])) # 10
print(find_max_value([-5, -2, -8, -1])) # -1
```
----
說明
```
max_value = float('-inf') 初始化 max_value 變數為負無窮大的值
這樣可以確保列表中的任何值都會比這個初始值大。
for num in numbers 是一個迭代給定的數字列表 numbers 中的每個元素。
if num > max_value 是一個條件判斷,檢查元素 num 是否大於當前已知的最大值 max_value。
如果是,則將 max_value 更新為 num。
函數返回最終的 max_value,即列表中的最大值。
```
---
最後的一題
~~這是一個超級複雜神秘高深晦澀超難的程式~~
但總攝覺得還好:D
----
### **計算1到200之間所有質數的平方和,並找出這個平方和的因數個數**
----
```py!
def is_prime(number):
if number <= 1:
return False
for i in range(2, int(number**0.5) + 1):
if number % i == 0:
return False
return True
def prime_square_sum(limit):
prime_sum = 0
for num in range(2, limit + 1):
if is_prime(num):
prime_sum += num ** 2
return prime_sum
def count_factors(number):
factors = 0
for i in range(1, int(number**0.5) + 1):
if number % i == 0:
factors += 2
if int(number**0.5) ** 2 == number:
factors -= 1
return factors
limit = 200
prime_sum = prime_square_sum(limit)
factor_count = count_factors(prime_sum)
print(f"1 到 {limit} 之間所有質數的平方和為:{prime_sum}")
print(f"這個平方和的因數個數為:{factor_count}")
```
----
```python
def is_prime(number):
if number <= 1:
return False
for i in range(2, int(number**0.5) + 1):
if number % i == 0:
return False
return True
```
```
這是一個判斷質數的函數。它接受一個整數 number 作為參數
返回一個布爾值,表示該數是否為質數。
```
----
```python
def prime_square_sum(limit):
prime_sum = 0
for num in range(2, limit + 1):
if is_prime(num):
prime_sum += num ** 2
return prime_sum
```
說明
```
這個函數 prime_square_sum 接受一個參數 limit
然後計算從 2 到 limit 之間的所有質數的平方和
在迴圈中,對每個質數,它將質數的平方累加到 prime_sum 變數中。
```
----
```python
def count_factors(number):
factors = 0
for i in range(1, int(number**0.5) + 1):
if number % i == 0:
factors += 2
if int(number**0.5) ** 2 == number:
factors -= 1
return factors
```
說明
```
這是一個計算一個數的因子數量的函數。它接受一個參數 number
然後通過迴圈檢查從 1 到 number 平方根的所有因子
在迴圈中,如果 i 是 number 的因子
那麼 factors 將增加 2
最後,如果 number 是一個完全平方數,需要減去 1(因為平方根只計算一次)。
```
----
```python
limit = 200
prime_sum = prime_square_sum(limit)
factor_count = count_factors(prime_sum)
print(f"1 到 {limit} 之間所有質數的平方和為:{prime_sum}")
print(f"這個平方和的因子個數為:{factor_count}")
```
說明
```
最後,程式設置了一個 limit 變數
然後調用 prime_square_sum 函數計算 1 到 limit 之間的所有質數的平方和
並調用 count_factors 函數計算這個平方和的因子數量
最終,打印出結果,包括質數的平方和以及這個平方和的因子數量。
```
---
今天就到這
上面的文字說明寫了好久 :skull:
~~好累~~
{"description":"能先幫我們填一下表單嗎","contributors":"[{\"id\":\"35a0644c-29d6-4dd3-98eb-9df68421a475\",\"add\":11910,\"del\":349}]","title":"解題"}