---
tags: Note
---
# 演算法

## 1. 緒論

### 定義:
針對一個問題，給予有限個明確的步驟，在有限時間內解出問題的方法

+ 每個步驟都要清晰明確
+ 輸入值域要清楚
+ 一種演算法可以用不同形式描述
+ 可能存在一種以上解決相同問題的演算法
+ 不同演算法對同一個問題有不同思路，花的時間也不一樣
+ 在有限時間內得到輸出
### 解決問題的程序:
理解問題 => 了解電腦設備的性能 => 決定精確解法或近似解法 => 確定適當的資料結構 => 設計演算法 => 詳細表述演算法 => 證明演算法正確性 => 分析演算法 => coding

### 重要的問題:
+ 排序
+ 搜尋
+ 字串處理
+ 圖問題
+ 組合問題
+ 幾何問題
+ 數值問題

### 基本資料結構
#### 線性資料結構
+ **array (有index)**
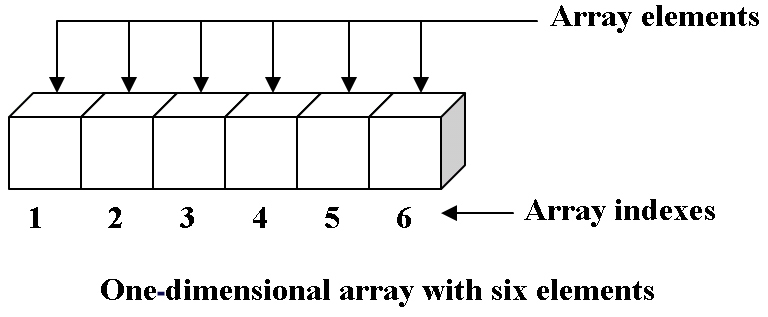
+ **linked-list (沒有index)**
+ **stack (後進先出)**
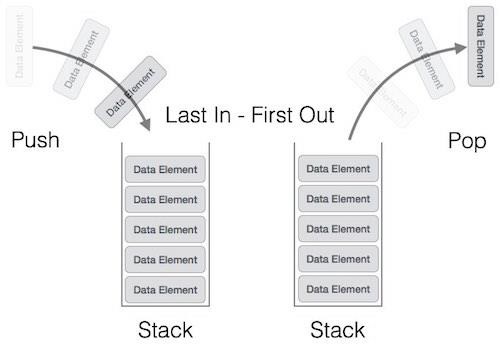
+ **queue (先進先出)**
+ 

#### 圖
+ 有向圖
+ 無向圖
+ 有根樹
+ 有序樹
+ 二元樹

#### 集合與字典

## 2. 演算法效率分析

$O()$ big-o (最大演算時間)
$O(n^2)$ 是 order of growth 小於 $n^2$
$\Omega()$ omega(最小演算時間)
$\Omega(n^2)$ 是 order of growth 大於 $n^2$
$\Theta()$ theta (平均演算時間)
$\Theta(n)$ 是 order of growth 等於 $n$

### 常見的 order of growth 類型：
1 常數
$log(n)$ 對數（sublinear）
$n$ 線性
$nlog(n)$
$n^2$ 平方
$2^n$ 指數

### 例子
#### binary search: $O(log_2n)$
最壞的狀況，假設有n個項，需要切x次
$\frac{1}{2}^x = n$，求x

#### bellman-ford algorithm （最短路徑）
假設有$m$個edge, $n$個node:
對edge做iteration
最壞為每次只更新一個node的權重 $\implies m\times n$

#### 行列式降階：
每次少一階：$\frac{n(n+1)}{2}$ => $O(n^2)$

## 3. 圖 Graph
- n 個 nodes (vertices)
- m 個 edges ($m \leq n^2$)

### 表示方式
#### adjacency list
- 空間 $O(n+m)$ （= input size）
- BFS, DFS 遇到用 adjacency list 表示的表示的 graph 時只需要 $O(n+m)$ 的時間複雜度

#### adjacency matrix
- 空間 $\Theta(n^2)$

### 無向圖 undirected graph
- connected: 是否 graph 內部任兩個 node 之間都有 path
#### Connected Component:
- 任兩個 node 之間都有 path 的最大集合
- 彼此之間沒有交集

### 有向圖 directed graph
- s-t 有 path != t-s 有 path
- Strongly connected: 是否 graph 內部任兩個 node 之間都有**雙向** path

#### Strongly Commected Component:
- 任兩個 node 之間都有**雙向** path 的最大集合
- 彼此之間沒有交集

### 廣度優先搜尋 BFS
- discover array: 當 BFS 找到一個 node $n$，discover($n$) = True
- Quene: first-in, first-out
- Layers: 初始 L(0) 只有起點 s，找到 node 就加入下一層

#### 實作
iterates over nodes in each layers，在 L(i) 內的 node $u$，找到 node $v$，檢查 discover($v$) 是否為 False，是的話：
- v 加入 L(i+1)
- (u, v) 加入 BFS Tree

#### BFS Tree
- BFS 找到的 nodes 和 經過的 edges
- BFS Tree 內的所有 nodes 一定是 connected component

### 深度優先搜尋 DFS
- explored array: 當對一個 node $n$ 做 DFS 時，explored($n$) = True
- Stack: last-in, first-out
- 和 BFS 不同： discover 時不做標記

#### 實作
- 用一個 Stack $S$ 搜集每次看到的 nodes
- iterate over $u \in S$，標記 explored，把所有和 $u$ 鄰接的 node 加入 $S$
- 直到 $S$ 空了

### 二分圖 Bipartite Graph
- 定義：所有 nodes 可以分為兩個子集使得所有 edges 兩端連接於不同子集
- 性質：
- 沒有 odd cycle （奇數 nodes 的圈）
#### Testing Bipartiteness of a Graph
- BFS
- 奇偶 Layer 標上不同顏色
- iterate over edges，檢查顏色是否都不同

### Directed Acyclic Graphs (DAGs)
- 沒有 cycle 的有向圖
- 有 topological ordering: 存在一種 nodes 排序使所有 edges 指向單一方向
- 優先權應用

#### 判斷是否為 DAG
- DFS，如果某次加入的 edge 的端點已經在 discover 內 $\implies$ 有環

#### 找一個 DAG 的 topological ordering
- set $S$：包含所有無 incoming edge 的 nodes
- $n = S.\text{pop}()$，把 $n$ 移除
- 檢查 $n$ 的 outcoming edges 鄰接 nodes 是否已無 incoming edge：
- 是：加入 $S$

## 4. 貪心法 Greedy algorithm
每一步都是最佳解，不能回溯修改

### 排程問題 Interval Scheduling Problem
- 同樣時間內排出最多行程
- 行不通的 Greedy rule：最早開始，最短結束，最少衝突
- 可行的：最早結束

#### 實作 $O(n\log{n})$
- 排序 ending time: $O(n\log{n})$
- 排程 $O(n)$

#### proof
和某個已知 optimal 比較，上述實作的第 i 個行程的結束時間一定比 optimal 的第 i 個還早

### 區間著色 Interval Partitioning (Coloring)
最少要幾個 Core 才能完成這些 Request
- 應用：伺服器問最少需要買的流量

#### 深度 $O(n\log{n})$
- 排序時間陣列 $s_1, s_2, s_3, f_2, f_1, s_4 .....$
- 深度： s:+1, f:-1
=> 最大深度 $d$（最糟所需要的 core 數）

#### 實作：塗色
labels: $1, 2, ..., d$
- 以開始時間順序：抓 labels
- 結束：吐出 labels

#### proof
1. 不會 overlap
2. 每個 request 都會被排到

### 最小延遲 Scheduling to Minimize Lateness
- 交作業問題
- 每個作業都有 deadline
- Lateness: $\max(0, f(i) - d_i)$
- No idle time (休息)

#### Greedy Rule
- 行不通的：最短時間先做，Slack = $d_i - t_i$ 最小先做
- deadline 早的先做

#### Exchange argument
- 抽換最佳解，最佳解仍是最佳解
- inversion: deadline 早的後做
- deadline 很晚的情況下，先做哪個沒差，所以可以有多種最佳解

### 最短路徑 Shortest path
- Dijkstra 算法 （j不發音）
- weights > 0
- 可以找出整張圖的 s 到任意一點 v 最短路徑

#### 實作
- set S = $\{\phi\}$
- $d_v$: 最短距離陣列
- 起點 s 加入 S
- 對每個圖裡且鄰接 S 的 node，找 S 到 node 的最短距離並儲存

### Huffman codes
- 最佳的 prefix codes（字根不重複）
- 每次合併頻率最小的字
- 左0右1
- $O(n\lg{n})$
- 可以用 BFS 以 $O(n+m) = O(2n-1) = O(n)$ 找出編碼

### kruskal's algorithm
+ 如果自kruskal及prim 中，把邊的權值調成負數，仍能正常運作嗎?
ANS: 可以，因為負值可以視為正值的平移，做完kruskal 之後再平移回來就好。
+ kruskal 做最小生成森林:
把圖分割，對每個分割做kruskal

### steiner problem
最短路徑和問題，可以加入平面上不存在的點 (steiner points)
每個 steiner point 的 degree 必須是 3
$\implies$ 120 度


### 渡河問題

a[0]+a[1]*2+a[n]
a[0]*2+a[n-1]+a[n]
每次選兩者比較取小的那個

## 費波那契 秤重問題
+ 砝碼只能放天平一邊: 2進位
+ 可以放兩邊: 3進位

# Divide and Conquer
## 主定理 master theorm
- $T(n) = aT(\frac{n}{b}) + f(n)$
- 判斷 $f(n)$ 是否增長比 $n^{\text{log}_ba}$ 快
- 慢：$\Theta(n^{\text{log}_ba})$
- 相等：$\Theta(n^{\text{log}_ba}\log{n})$
- 快：$\Theta(f(n))$

## Tromino puzzle
- [play this](https://www3.amherst.edu/~nstarr/trom/puzzle-8by8/)
- 用小 L 拼出大 L

# Dynamic Programming

## world cup series
- A, B 兩隊一直比賽，A勝率p，當A剩下i場要贏，B剩下j場要贏時，A的勝率為 P(i,j)
- P(i,j) = (1-p)P(i,j-1) + pP(i-1,j)

digraph hierachy {
"P(i, j)"->"P(i-1, j)" [label=p]
"P(i, j)"->"P(i, j-1)" [label="1-p"]
}

## Warshall 演算法
- 遞移封閉集　transitive closure
- 十字檢查：a$\to$b 和 b$\to$c 有路徑$\implies$a$\to$c 有路徑$\implies$改成$1$

digraph {
c
b -> d
d -> c [constraint=false]
d -> a [constraint=false]
{rank = same; a -> b;}
{rank = same; c; d;}
 }

**(1)鄰接矩陣**
$$\begin{matrix}
& a & b & c & d \\
a & 0 & 1 & 0 & 0 \\
b & 0 & 0 & 0 & 1 \\
c & 0 & 0 & 0 & 0 \\
d & 1 & 0 & 1 & 0
\end{matrix} \tag{1}$$

**(2)遞移封閉集**
$$\begin{matrix}
& a & b & c & d \\
a & 1 & 1 & 1 & 1 \\
b & 1 & 1 & 1 & 1 \\
c & 0 & 0 & 0 & 0 \\
d & 1 & 1 & 1 & 1
\end{matrix} \tag{2}$$
## Floyd 演算法

digraph {
a ->b [style=invis]
{rank = same; b -> a [label=2];}
{rank = same; c -> d [label=1];}
a -> c[label=3]
d -> a[label=6]
c -> b[label=7]
}

**(1) 加權矩陣**
$$\begin{matrix}
& a & b & c & d \\
a & 0 & \infty & 3 & \infty \\
b & 2 & 0 & \infty & \infty \\
c & \infty & 7 & 0 & 1 \\
d & 6 & \infty & \infty & 0
\end{matrix} \tag{2}$$

**(2) 距離矩陣**
$$\begin{matrix}
& a & b & c & d \\
a & 0 & 10 & 3 & 4 \\
b & 2 & 0 & 5 & 6 \\
c & 7 & 7 & 0 & 1 \\
d & 6 & 16 & 9 & 0
\end{matrix} \tag{1}$$

- 完全最短路徑問題

## P,NP, NP-complete

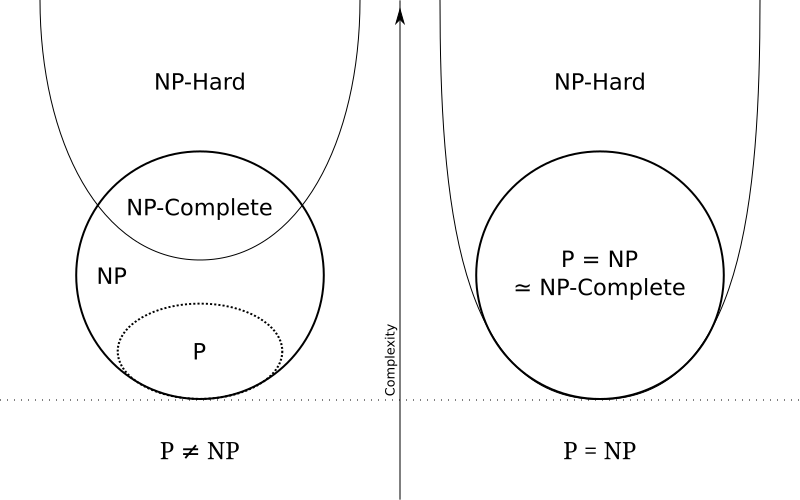
+ P問題(polynomial)
可以在多項式時間複雜度 $O(n^k)$ 內求解的問題
+ NP問題(non-deterministic polynomial)
可以在多項式時間複雜度內驗證答案是否正確的問題
+ NP-hard
只要有一個NP困難問題找到P解，那麼所有NP問題都是P問題
### NP-Complete
- 條件1: 本身為NP
- 條件2: 所有 NP 問題都可以 reduce 成 NP-Complete
- A 可以被 reduce 成 B: $A \leq_p B$ 代表可以用B的解法來解A（但是不一定可以用A的解法來解B），所以B至少跟A一樣難
- NP-Complete 問題至少跟 NP 問題一樣難
- NP-Complete 的解法可以用來解所有 NP 問題
- 如果證明 NP-Complete 問題有 P 時間解，即 P = NP