In October 3, 2016, Vitalik Buterin, a guy who funded a little an no so well-known blockchain called Ethereum, did [a post in reddit](https://www.reddit.com/r/ethereum/comments/55m04x/lets_run_onchain_decentralized_exchanges_the_way/) proposing to run the first DEX based on uniswap famous invariant $x \times y = k$.

But, what does this invariant means? Well, it is just a rectangle area... I'm not joking.

How would you calculate next rectangle area?

$$Rectangle \; area = shorter \; side \; length \times longer \; side \; length$$

Now, let's suppose that we want modelize all the rectangles which have a fixed area, for instance 10. How would this model look like? Well, something like this:
1. $shorter \; side \; length > 0$
2. $longer \; side \; length > 0$
3. $shorter \; side \; length \times longer \; side \; length = 10$

Now, let's make the formula a little more general. If I give you an area $k$ with $k>0$, which would be its formula?
$$shorter \; side \; length \times longer \; side \; length = k$$

Instead of talking about the $shorter \; side$ or the $longer \; side$, we could also talk about the $bottom \;side$ and the $left \;side$, given that **both of them are going to have the different length except from when they form a square**. Then

$$bottom \; side \; length \times left \; side \; length = k$$

And if we say that $x = bottom \; side \; length$ and we $y = left \; side \; length$ we reach to next formula:

$$ x \times y = k$$

Can we graph this? The answer is absolutely yes!

<iframe src="https://www.geogebra.org/calculator/thcaar5d?embed" width="800" height="600" allowfullscreen style="border: 1px solid #e4e4e4;border-radius: 4px;" frameborder="0"></iframe>

The green ecuation, when $x >0$ and $y>0$ represent the area of the rectangle which area is $k$

# $x$ and $y$ meaning
In the context of uniswap:
* $x$ is the amount of token $X$ in the liquidity pool represented by $x \times y = k$
* $y$ is the amount of token $Y$ in the liquidity pool represented by $x \times y = k$

How many tokens $Y$ are per token $X$ in a pool? Simply $\frac{y}{x}$. This could be consider as the price of token $X$ in terms of token $Y$ in a pool in a given moment. Uniswap describe this as the price of token $X$ in units of token $Y$, however is this really the price?

# Swap without fees
To perform a swap, uniswap enforce that after the operation

$$x_{before \; swap} \times y_{before \; swap} = x_{after \; swap} \times y_{after \; swap} = k$$

However, how is this granted?

If we want to get $900$ tokens $X$, how much tokens $Y$ should we sent? If we think that $\frac{y}{x}$ is the price of token $X$ in terms of token $Y$ we could argue that it is $900 \times \frac{y}{x}$, but we have 2 problems:
* If $900 \times \frac{y}{x} > x$ then there won't be enough token to perform the operation.
* This does not guarantee that after adding $900$ tokens $Y$ and extract $900 \times \frac{y}{x}$ tokens $X$ from the pool the invariant $k$ will hold.

For instance let's suppose that we have $1,000$ tokens $X$ and $1,000$ tokens $Y$, then:

1. Initially: $x \times y = 1,000 \times 1,000 = 1,000^{2} = 1,000,000$. So $k = 1,000^{2} = 1,000,000$
2. $\frac{y}{x} = \frac{1,000}{1,000} = 1$
3. $900 \times \frac{y}{x} = 900 \times 1 = 900$
4. If we add 900 tokens $Y$ to get 900 tokens $X$, then:
* $x_{after \; swap} = x_{before \; swap} - amountOut_{X} = 1,000 - 900 = 100$
* $y_{after \; swap} = y_{before \; swap} + amountIn_{Y} = 1,000 + 900 = 1,900$
* However: $x_{after \; swap} \times y_{after \; swap} = 100 \times 1,900 = 190,000$. Given that $1,000,000 \neq 190,000$ we can see that $x_{before \; swap} \times y_{before \; swap} \neq x_{after \; swap} \times y_{after \; swap}$, therefore $k$ does not holds.

So using $\frac{y}{x}$ to calculate how much should we get is not a correct approach. But, given we know current $x$ and $y$ amount, how much tokens $X$ we are introducing to the pool, and the value $k$ that must hold we know that:
* $y_{after \; swap} = y_{before \; swap} + \Delta y$, with $\Delta y$ as simply the difference of $y_{after \; swap} - y_{before \; swap}$.
* $x_{after \; swap} = x_{before \; swap} + \Delta x$, with $\Delta x$ as simply the difference of $x_{after \; swap} - x_{before \; swap}$.

If we are subtracting $amountOut_{X}$ tokens from the pool, then
$$x_{after \; swap} = x_{before \; swap} + \Delta x \implies$$
$$x_{after \; swap} = x_{before \; swap} - amountOut_{X} \implies$$

$$\Delta x = - amountOut_{X}$$

This value also can be expressed as $- amountOut_{X} = x_{after \; swap} - x_{before \; swap}$

Now we can deduce that
$$x_{before \; swap} \times y_{before \; swap} = k \implies$$
$$ (x_{before \; swap} + \Delta x) \times (y_{before \; swap} + \Delta y) = k \implies $$
$$ y_{before \; swap} + \Delta y = \frac{k}{(x_{before \; swap} + \Delta x)} \implies $$
$$ \Delta y = \frac{k}{(x_{before \; swap} + \Delta x)} - y_{before \; swap} \implies $$
$$ amountIn_{Y} = \frac{k}{(x_{before \; swap} + \Delta x)} - y_{before \; swap} \implies $$

Let's see if this work for our example:
$$amountIn_{Y} = \frac{k}{(x_{before \; swap} + \Delta x)} - y_{before \; swap} $$
$$amountIn_{Y} = \frac{1,000^{2}}{(1,000 - 900)} - 1,000 $$
$$amountIn_{Y} = \frac{1,000,000}{(100)} - 1,000 $$
$$amountIn_{Y} = 10,000 - 1,000 $$
$$amountIn_{Y} = 9,000 $$

Wait!! We need to give $9,000$ $Y$ tokens to get $900$ $X$ tokens? Wouldn't that mean a real price of $10$ $Y$ tokens per $X$ token? Yes, but in this way the invariant will hold:

$$(x_{before \; swap} + \Delta x) \times (y_{before \; swap} + \Delta y) =$$
$$(1,000 + 9,000) \times (1,000 - 900) =$$
$$10,000 \times 100 = 1,000,000 = 1,000^{2}$$

# Swap with fees
When a swap is executed a fee is charged to compensate liquidity providers. In uniswap V2 this fee is 0.30%, and it is paid in the token we are sending.

$$feesToPay = amountSent_{Y} \times fee \; percentage \%$$

How does this affect the swaps and $k$?

To perform a swap:
* $amountIn_{Y} = amountSent_{Y} \times (1 - fee \; percentage \%)$

This is the amount that we are going to use to calculate how much $amountOut_{X}$ a user is going to receive for sending $amountSent_{Y}$. Fees are added as liquidity inside the liquidity pool, this means that:

* To perform the swap we are going to consider $k$ before the transaction and $amountIn_{Y}$. $k_{before \; swap}$ is used to calculate $amountOut_{X}$. In this way: $(x_{before\; swap} - amountOut_{X}) \times (y_{before \; swap} + amountIn_{Y}) = k_{before \; swap}$
* We will need to update $k$ after the swap based on $amountSent_{Y}$ and $amountOut_{X}$. This means that: $(x_{before \; swap} - amountOut_{X}) \times (y_{before \; swap} + amountSent_{Y}) = k_{after \; swap}$

Notice that in the first case we use the amount of token $Y$ that we sent discounting fees, and in the second case we don't discount fees. Also, in both cases $amountOut_{X}$ does not change. This enable fees to autocompound in each swap operation

# Problems with V2
Uniswap V2 approach is super simple and efficient for on-chain calculations, at least once you get it (hopefully you do now after this article :D). However, it is not efficient for liquidity providers. Why? Liquidity providers are enforced to provide liquidity for whole price range, which can motivate a lot of liquidity to not be used.

In our example, of $1,000$ tokens $X$ and $1,000$ tokens $Y$, let's suppose that $X$ was USDC and $Y$ was USDT. In normal circumstances, why would anyone want to get $900$ USDC for $9,000$ USDT paying $9$ USDT per USDC? Would it not be more reasonable to offer them at a price of at most $1.05$ USDT per USDC? In this way we can get more fees, otherwise anyone can simply go to another AMM with more liquidity.

Before uniswap V3, an order book was the only way to handle this problem (or at least the only one I could find). An order book looks something like this:


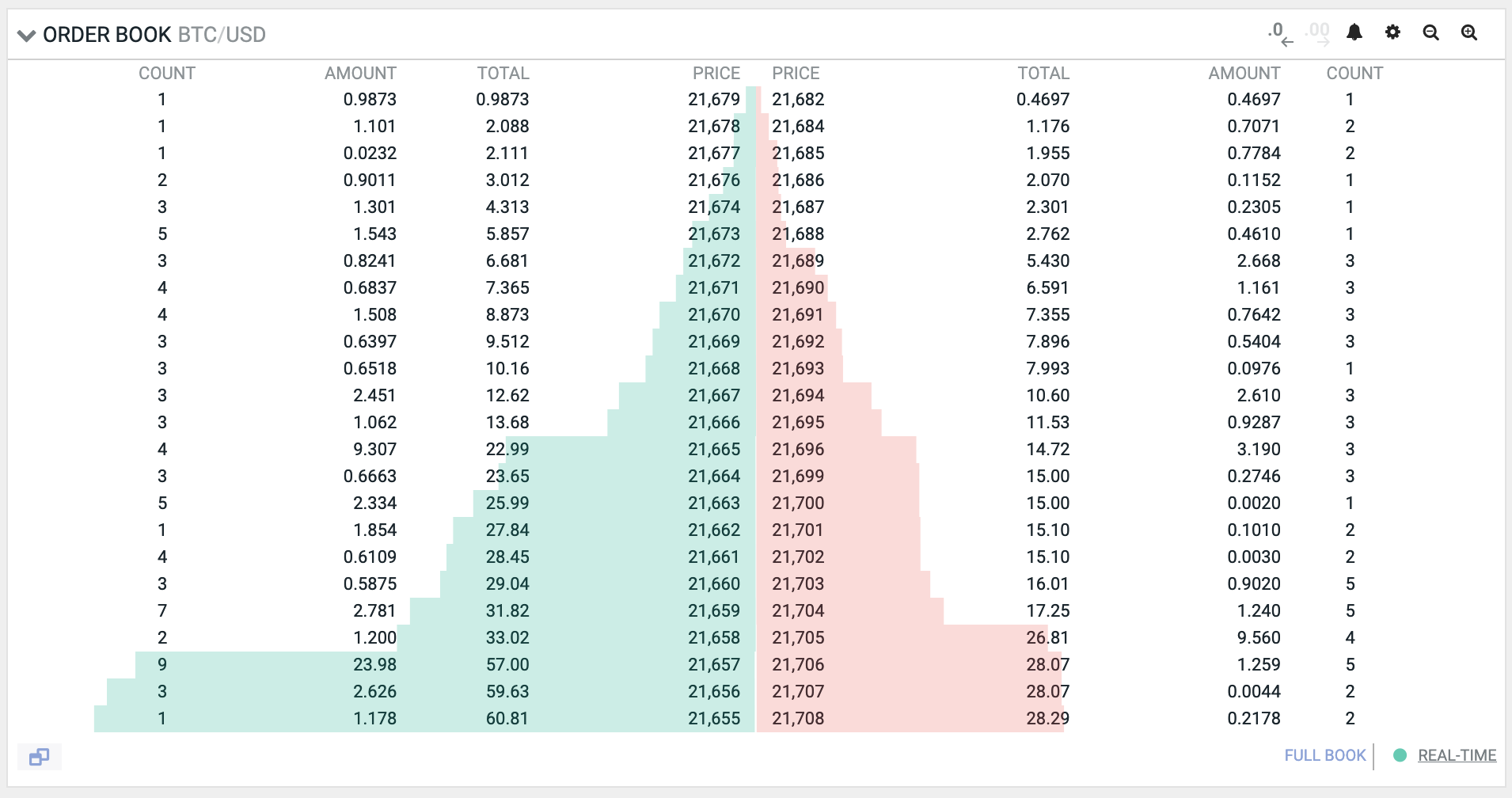
The column price indicates the price to trigger an order, the bars represent how much liquidity there is available. Usually liquidity concentrates around current price. To perform a swap users specify how much is the most they are willing to pay/receive if they are buying/selling. Then they try to consume the orders with the lowest/highest price, and the next one if the liquidity is not enough.

You may be thinking: "So, why not simply implement an order book on chain? The algorithm to perform a buy/sell doesn't seems so complex". It is an option, but when you put an order you would be only willing to sell for the price you specified, not a price range. For instance, something you cannot do is putting a sell order to accept selling BTC between 40-45k.

So, during [next article](https://hackmd.io/@carlitox477/SyxVHD4kC) we are going to talk about how uniswap V3 solved this.