## 4章 特徴量と予測値の関係性を知る 〜Partial Dependence〜 『機械学習を解釈する技術』輪読回 2021年10月30日（土） S.Kanai --- ### 🔖 4.1 なぜ特徴量と予測値の関係性を知る必要があるのか * 3章のPFIで求めるような **重要度** では、特徴量が変化した時の予測値の動きが分からない。 * 4章のPDは、特徴量と予測値の **関係の大枠** を知ることができる。 例 * PFI : アイスの売り上げ予測には、気温が重要である * PD : 気温が高くなると、アイスの売り上げの予測値が高くなる ----  https://travel.watch.impress.co.jp/docs/news/1325186.html ---- PDの用途 * モデルのデバッグ - PDの傾向は常識と一致するか？ - 例 : 気温が高いとアイスが売れなくなるモデルはバグの可能性 * 意思決定の仮説 目的変数を最大化するように変数を操作する - 例 : 広告出稿料が高いとアイスの売り上げが高いなら、広告出稿料を増額する - 注 : PDは因果関係を示すとは限らないので、↑のような仮説を因果推論で確かめるのが良い --- ### 🔖 4.2 線形回帰モデルと回帰係数 * 線形回帰モデルは、回帰係数がそのまま特徴量と予測値の関係を示す。 - しかし、非線形な関係は正確に記述できない。 * Random Forest（等の非線形モデル）は、非線形な関係も学習できる。 - しかし、回帰係数のように特徴量と予測値の直接的な関係は取り出せない。 ---- 参考 : Random Forest の原理  https://www.researchgate.net/figure/Random-Forest-Principle-17_fig1_325966978 --- ## 🔖 4.3 Partial Dependence ---- ### 4.3.1 1つのインスタンスの特徴量とモデルの予測値の関係 あるインスタンスに注目して、特徴量を動かした時の予測値の動きを可視化する。 不正会計検知モデルでの例 1. とある会社の財務情報を1つ選ぶ 1. 興味のある特徴量 **以外の** 特徴量の値を固定する 1. 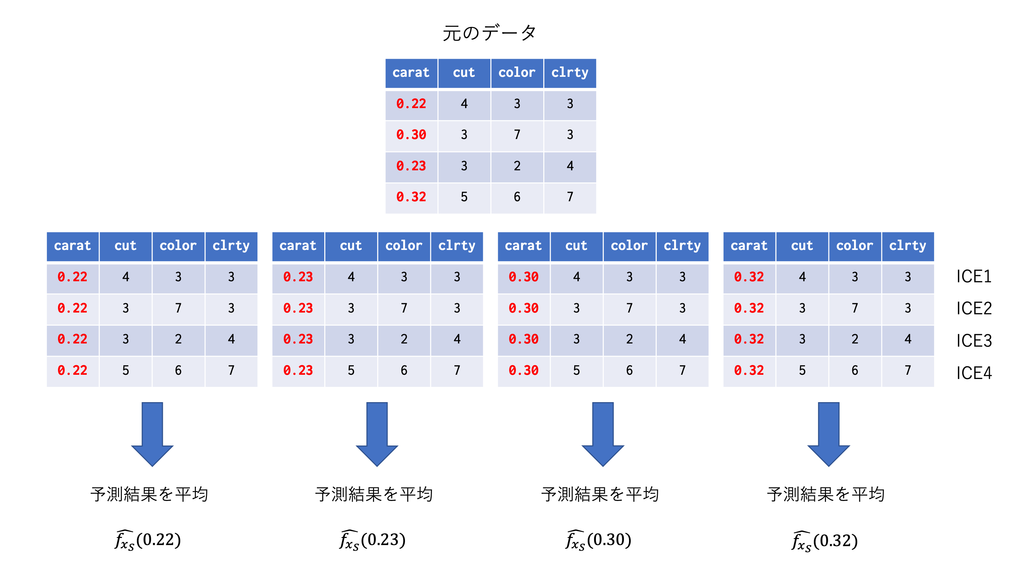興味のある特徴量の値を **変化させて** 、その都度の **予測値** をプロットする ---- ### 4.3.2 すべてのインスタンスに対する特徴量と予測値の平均的な関係 すべてのインスタンスの、特徴量を動かした時の予測値を、特徴量の値ごとに平均する。 不正会計検知モデルでの例 1. 全てのデータセットを利用する 1. 興味のある特徴量 **以外の** 特徴量の値を固定する 1. 興味のある特徴量の値を **変化させて** 、その都度の **予測値の平均値** をプロットする これが、Partial Dependence ----  https://dropout009.hatenablog.com/entry/2019/01/07/124214 ---- ### 4.3.3 Partial Dependence クラスの実装 (省略) ---- ### 4.3.4 Partial Dependence の数式表現 モデルの興味のある特徴量の周辺分布。すなわち、特徴量にある値を入れた時の、平均的な予測値を表す。 $$ PD_j\left(x_j\right)= E\left[\hat{f}\left(x_j, \bf{X}_{\\\j}\right)\right] \\ = \int\hat{f}\left(x_j, \bf{x}_{\\\j}\right)p\left(\bf{x}_{\\\j}\right) d\bf{x}_{\\\j} $$ ---- ※興味のあるもの以外の特徴量ベクトルを、母集団の分布に従うように発生させたいので、元データをそのまま使っている。 なので、母集団の分布が使えるならば、それに従う乱数で特徴量ベクトルを生成すれば良い。多くのデータを生成すればPDの精度が上がると思う。 --- ## 🔖 4.4 Partial Dependence は因果関係として解釈できるのか ---- ### 4.4.1 シミュレーション3 : 相関関係と因果関係 * 目的変数と特徴量の散布図では、相関のある他の特徴量の影響が排除されない。 * 上手く学習ができているモデルのPDプロットは、特徴量同士の影響が排除された結果を示す。 ----   ---- ### 4.4.2 PDを因果関係として解釈することの危険性 * モデルに投入されていない変数の影響は、PDを使っても排除できない。 * PDの結果を、目的変数と特徴量の **因果関係** として解釈することは危険。 * PDの結果を、目的変数と特徴量の **平均的な関係** として解釈することは安全。 --- ### 🔖 4.5 実データでの分析 * ボストン住宅価格データセット - 目的変数 : 住宅価格 - 特徴量 : 部屋の数, 都心からの距離, 犯罪率, 他 - モデル : ランダムフォレスト ---- ### 4.5.1 PDによる可視化 * 部屋の数が多いと、住宅価格が高い。 * 都心からの距離が遠いと、住宅価格が低い。 ---- ### 4.5.2 散布図による可視化 * 都心からの距離が遠いと、住宅価格が高い。 - PDの結果と異なり、直感にも反する。 * （実は）都心からの距離が遠いと、犯罪率が低い。 * 犯罪率が低いと、住宅価格が高い。 ----   ---- PDは、散布図では捉えられない背後関係を排除できる。 --- ### 🔖 4.6 PDの利点と注意点 利点 * どんな機械学習モデルでも使える * 特徴量の予測値への影響の与え方が知れる * 非線形な関係も把握できる * 他の特徴量の影響を考慮している ---- 注意点 * 見ている関係は、あくまで特徴量と **予測値** （$\neq$目的変数の値） * 見ている関係は、特徴量と予測値の **平均的な** 関係 個別のインスタンスにおける関係性は、5章ICEで見れる --- ### 🔖 考察 * 会計不正検知での実用では、モデルの説明のために使えそう。論文や監査法人への営業資料で見せるイメージ。 * GPFIで重要度の高い特徴量グループに興味がある場合は、グループの組み合わせでPDを計算するとよさそう。 * カテゴリ変数でもPDは利用できそう。全てのカテゴリ実現値を代入して、予測させる。 ---- * [PDの解説資料](https://web.stanford.edu/~hastie/Papers/ESLII.pdf) p.388 - ↑はscikit-learn(Pythonの機械学習ライブラリ)の[PD使用例のページ](https://scikit-learn.org/stable/auto_examples/inspection/plot_partial_dependence.html#sphx-glr-auto-examples-inspection-plot-partial-dependence-py)に記載あり。