# CR point ENSTA 12-13/04/2023

Présents : Alain, Jean-Baptiste, Christian, Mathieu, @abavoil @jbcaillau (ENSTA Bretagne)

## Contexte
- modèle 3D = corps rigide *vs.* point-mass (point ponctuel) actuellement
- origine = projet "beyond the sea" (navigation par kite)
- technos anciennes / actuelles : Kite Power, KiteGen, SkySails (kite à caisson)
- [années 80 Lloyd](http://edge.rit.edu/edge/P15462/public/CAD/crosswind_kite.pdf)
- montée par des 8, puis redescente : techno existante
- surface kite 20-30 m^2
- 0.6 kW / m^2
- coût a priori un peu caché / non négligeable pour la commande du kite

## Techno KEEP
- ossature = kite à boudins (moins de brides, donc moins de traînée)
- dimensions : jusqu'à 300 m^2, 100 m de haut
- aller chercher des vents forts plus haut
- monter jusqu'à 1 kW / m^2
- kite 20 m^2 = équivalent à éolienne 25 kW (à hauteur fixe de 15 m env)
- 2 lignes avant + 2 lignes arrière (pilotage)
- le 8 engendre une rotation de la "tourelle" au sol
- commande par lignes arrière
- viser un système auto-entretenu
- modèle = 1 seule ligne (et non 4) de longueur constante vers une masse ponctuelle
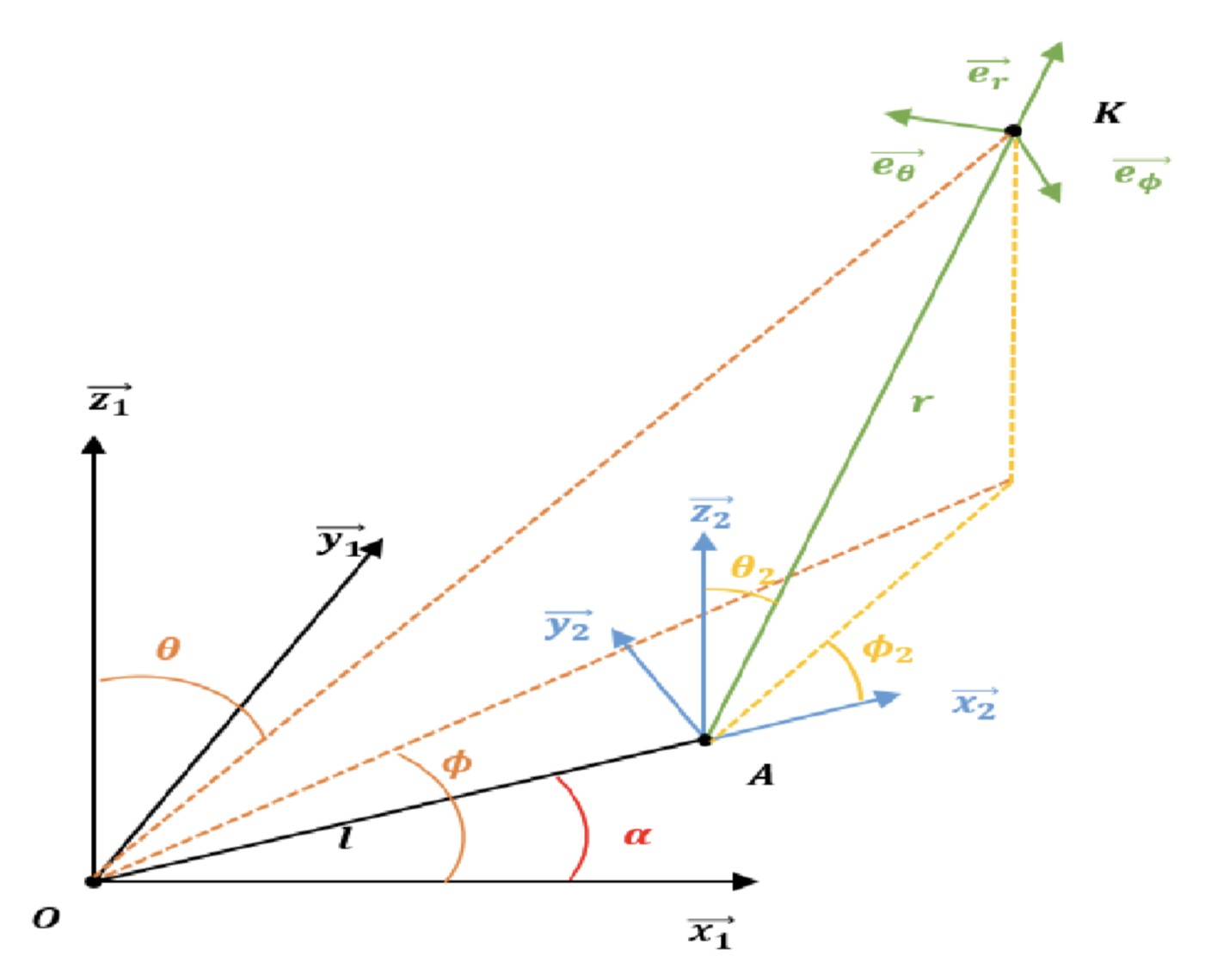
- $\alpha$ = angle du bras, $(\theta,\phi)$ coords sphériques usuelles (sans homothétie = distance kite), sachant que le point $A$ (de fin du bras)
- 2 jeux de coords : $(\alpha,\theta,\phi)$ (attaché à $O$), $(\alpha,\theta_2,\phi_2)$ (attaché à $A$), sachant que $OA$ et $AK$ sont des longueurs fixes
- $(e_r,e_\theta,e_\phi)$ trièdre direct lié aux coords sphériques
- contrainte : le kite est astreint à rester sur le cône (non convexe) engendré par une courbe de huit en $(\theta,\phi)$


<img width="677" alt="IMG_2033" src="https://user-images.githubusercontent.com/62183989/231583635-4c47e27c-8ea0-4648-9fac-fc8efd8cdcec.png">

- vent : la principale composante est horizontale (1 ou plusieurs ordres de grandeur en moins pour composante verticale
- $(0x_1y_1)$ est un repère vent, *i.e.* $(0x_1)$ est la direction du vent
- le modèle intègre donc, par construction, le fait que la direction du vent est fixe
- raffinement : vent non constant, repère mobile
- couple $C_{aero}$ en fonction de $\dot{\alpha}$ : impact à la fois sur la dynamique et sur le coût (= énergie générée)
- forme "libre" dans le régime $|\dot{\alpha}|$ dans $[\dot{\alpha}_\min, \dot{\alpha}_\max]$, et le couple max (données génératrice)
- ce couple max (que la génératrice peut encaisser) est une contrainte
- modèle 3D, *i.e.* solide *indéformable* (c'est encore une approximation) : permet de prendre en compte non pas une seule ligne ($AK$) mais un différentiel ligne avant / ligne arrière
- contrainte aussi sur la tension de la ligne (= pression supportée par le kite)
- puissance instantanée = $C_{aero} \times \dot{\alpha}$
- paramètres fixes : longueur ligne $r$, longueur bras $l$, $\Delta\theta$, $\Delta\phi$ du cycle
- coût = énergie (intégrale de la puissance instantanée)
- $C_r = C_{aero}$ (fonction de $\dot{\alpha}$)
- model mass point : ajouter calcul suppl. (énergie...) et faire (i) comparaison `python`/ `julia`, (ii) prédicteur-correcteur
- pour mémoire : puissance instantanée = $C_r \dot{\alpha}$, *cf.* code `python`
- état "vrai" : $(R,\tau)$ où $R = OK$, dimension deux (cône), et ordre deux : dim quatre, donc

## Modèle corps solide
- modèle corps solide (indéformable) : état dim 2 + 3 nouveaux degrés de liberté (SO(3)) = 5 ; donc au moins 2 x 5 = 10 (cf. ordre deux)
- contrôle dim ? 2 = les longueurs des deux lignes arrière (ou $\frac{l_1 - l_2}{2}$ et $\frac{l_1 + l_2}{2} - l_{avant}$)
- question ouverte : faisabilité suivi trajectoire en huit "sans commande", *i.e.* avec lignes fixes
- première approximation : modèle stationnaire pour $C_L$ et $C_D$ (lift = portance, drag = traînée) en fonction de l'angle d'incidence (donné par attitude)
- plus fin : modèle instationnaire

## Todo
- [x] préalable : normalisation système, *cf.* [théoreme de Vaschy-Buckingham](https://fr.wikipedia.org/wiki/Théorème_de_Vaschy-Buckingham)
- [ ] vérif. calculs via [symbolique](https://symbolics.juliasymbolics.org/stable/manual/derivatives/)
- [ ] passer à un code prédicteur-correcteur pour vérifier qu'on a juste un drift (et pas une diffusion sur le cône) ; voir [ici](https://github.com/SciML/DiffEqCallbacks.jl)
- [ ] tester différentes conditions initiales (cas où le kite ne décrit qu'une partie du huit, revient en arrière...)
- [ ] générer le second membre par diff. auto. (*cf.* dérivation des contraintes)
- [ ] paramètres à optimiser : $I_\mathrm{eq}$ (inertie du bras), longueur de ligne (ou bras, ou ratio, *cf.* ci-dessous), $\Delta\theta$, $\Delta\phi$
- [ ] revoir (*cf.* pertinence de la mise à zéro au delà du couple du couple max) et optimiser la loi (forme feedback) $C_r(\dot{\alpha})$ (prendre un modèle paramétrique)
- [ ] intégrer (= dans un premier temps monitorer sur simu, éventuellement avec callback, puis dans un cadre optimisation) les contraintes (i) $F_\mathrm{tract}$ maximum *cf.* (17)), (ii) couple maximum pour génératrice
- aussi : contrôle = forme du huit (courbe de Lissajous, sinon), ce qui est une façon de faire du contrôle en mass point
- prochain point : mi / fin mai

## Misc
- revoir biblio Moritz *et al* (ancienne techno ?) [review](https://scholar.google.com/citations?view_op=view_citation&hl=en&user=JEwMX6wAAAAJ&citation_for_view=JEwMX6wAAAAJ:1taIhTC69MYC)
- paramètres = ? dim finie / infinie
- conditions de vent, géographie typique (montagne... cf. appli défense)

## Jour 1

- ~80% de la tension sur les lignes avant, contrôle avec les lignes arrière : trainée créée en déformant le profil lorsqu'on tire sur la ligne.
- opposition de phase kite/bras de la génératrice pour un contrôle autonome ? Test avec un modèle plus simple de pendule double excité ? [https://en.wikipedia.org/wiki/Parametric_oscillator](https://en.wikipedia.org/wiki/Parametric_oscillator) avec entrée d'énergie par le vent et sortie par la génératrice ?
- *Question* Quelle est l'amplitude optimale du mouvement du bras ($\alpha$) ? Quel phase avoir entre $\phi$ et $\alpha$ : privilégier un contrôle presque passif, avoir un angle proche de 90° entre le bras et les lignes, ou les deux ?
- $0 < F_\mathrm{tract} < F_\mathrm{tract, max}$ et $C_r < C_\mathrm{r, max}$ : le kite doit toujours être sous tension, sans dégrader l'équipement -> choquer en cas de vent trop fort. $F_\mathrm{tract, max} = 100\ kg/m^2 \cdot 9.81 N/kg$.
- [Rapport_modele_dynamique_V5.pdf](docs/Rapport_modele_dynamique_V5.pdf#page=8) eq. 17 sert à calculer $F_\mathrm{tract}$ que l'on injecte dans les autres équations.
- Puissance environ proportionelle au cube de la vitesse du vent
- Possibilité de lisser la courbe de puissance instantanée avec une transmission mécanique par train épicycloïdal entre tourelle et génératrice ?

## Jour 2
- Point K au quart de la corde du kite
- Hypothèse pour le calcul de $C_L$ et $C_D$ : le kite est toujours aligné avec le vent apparent, il n'avance pas en crabe (à vérifier)
- **Angle d'incidence** : pour une incidence faible, L (portance) est environ deux ordres de grandeurs plus grand que D (trainée). Dans [Fagiano 2009](docs/fagiano-2009a.pdf#page=61), l'angle d'incidence varie entre 4° et 12° en phase de production, avec des pics à -2° et à plus de 16°. La polaire de $C_L$ calculée est affine jusqu'à 16°, et le décrochage a lieu à 20°. **Moyenne à 8°** d'après [Fagiano 2009](docs/fagiano-2009a.pdf#page=61).
- vérifier que $\dot \alpha$ ($\alpha$ = incidence ici) est faible (par rapport à quoi) pour avoir le droit de considérer $C_L(\alpha)$ au lieu de $C_L(\alpha, \dot \alpha)$
- Analyse dimensionelle : trouver des grandeurs adimensionelles, par exemple $r/l$, $V/\sqrt{g l}$, en prenant $l$, $m$ et $g$ comme base de variables dimensionnellement indépendantes ?