# 不同程式語言特性範例

# 矩陣鏈乘積 Python TLE

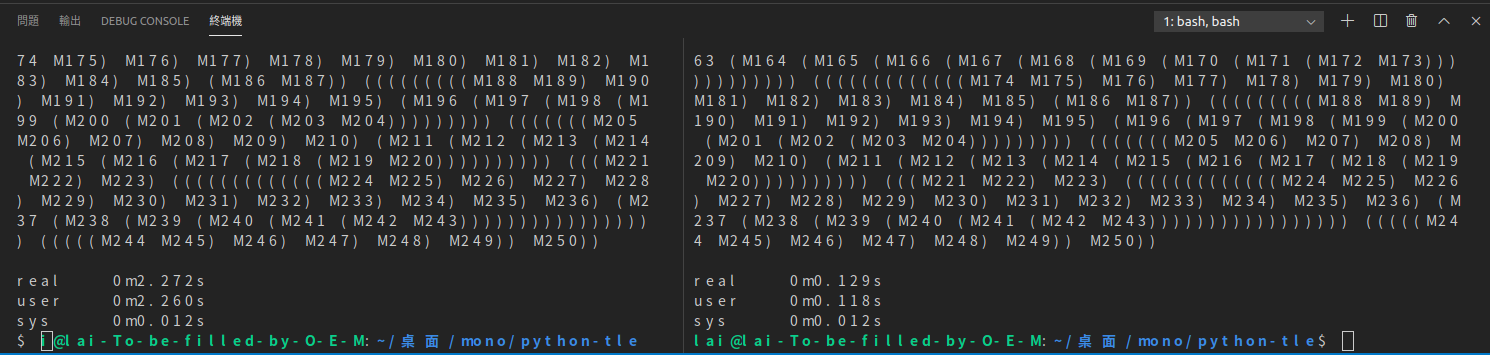
左邊是Python 右邊是VB
<!--  -->

## javascript create test data

function createTestData(n){
    let min = 2;
    let max = 30;
    
    let row = Math.floor(Math.random() * (max-min+1)) + min;
    let output = [n.toString()];
    for(let i = 1; i <= n; i++){
        let col = Math.floor(Math.random() * (max-min+1)) + min;    
        output.push(`${row} ${col}`);
        row = col;
    }
    return output.join('\n');
}

## input data:

3
5 10
10 20
20 35
2
10 20
20 35
6
30 35
35 15
15 5
5 10
10 20
20 25
100
7 29
29 6
6 8
8 27
27 26
26 30
30 27
27 18
18 15
15 3
3 27
27 24
24 9
9 23
23 30
30 13
13 12
12 11
11 28
28 7
7 21
21 7
7 10
10 28
28 16
16 10
10 18
18 25
25 8
8 30
30 17
17 11
11 12
12 5
5 29
29 8
8 2
2 25
25 7
7 17
17 13
13 18
18 5
5 22
22 25
25 9
9 21
21 5
5 4
4 16
16 14
14 2
2 5
5 2
2 6
6 17
17 12
12 15
15 26
26 11
11 21
21 15
15 28
28 17
17 28
28 29
29 6
6 25
25 13
13 10
10 29
29 5
5 17
17 17
17 6
6 7
7 30
30 19
19 27
27 3
3 13
13 18
18 8
8 15
15 18
18 25
25 16
16 30
30 8
8 2
2 4
4 13
13 15
15 29
29 16
16 19
19 18
18 12
12 3
3 2
250
22 4
4 26
26 26
26 18
18 27
27 15
15 12
12 4
4 29
29 13
13 20
20 3
3 2
2 19
19 20
20 9
9 17
17 30
30 9
9 10
10 17
17 4
4 4
4 19
19 12
12 25
25 6
6 13
13 22
22 12
12 26
26 2
2 3
3 17
17 3
3 19
19 24
24 12
12 28
28 24
24 24
24 3
3 22
22 3
3 21
21 11
11 12
12 10
10 4
4 27
27 5
5 27
27 6
6 17
17 27
27 3
3 30
30 24
24 20
20 6
6 9
9 24
24 20
20 24
24 2
2 29
29 26
26 30
30 18
18 21
21 5
5 26
26 6
6 21
21 19
19 13
13 29
29 5
5 14
14 3
3 9
9 15
15 28
28 14
14 20
20 12
12 9
9 22
22 12
12 3
3 22
22 16
16 15
15 17
17 18
18 15
15 27
27 3
3 28
28 10
10 5
5 7
7 15
15 28
28 14
14 25
25 14
14 14
14 4
4 2
2 15
15 12
12 9
9 16
16 14
14 11
11 20
20 4
4 2
2 17
17 19
19 18
18 5
5 30
30 13
13 9
9 4
4 8
8 20
20 30
30 8
8 7
7 9
9 8
8 20
20 27
27 20
20 22
22 7
7 15
15 7
7 21
21 22
22 20
20 6
6 9
9 15
15 26
26 17
17 29
29 21
21 17
17 15
15 28
28 19
19 24
24 13
13 26
26 2
2 23
23 4
4 13
13 20
20 25
25 5
5 18
18 10
10 4
4 19
19 29
29 15
15 6
6 2
2 13
13 8
8 15
15 10
10 25
25 13
13 28
28 16
16 27
27 25
25 18
18 4
4 27
27 2
2 18
18 12
12 28
28 20
20 12
12 18
18 21
21 4
4 18
18 30
30 7
7 28
28 10
10 27
27 14
14 6
6 2
2 17
17 21
21 15
15 30
30 23
23 7
7 28
28 25
25 23
23 11
11 24
24 14
14 25
25 17
17 22
22 2
2 13
13 9
9 2
2 16
16 22
22 16
16 4
4 11
11 9
9 9
9 10
10 22
22 21
21 26
26 20
20 3
3 27
27 19
19 30
30 23
23 30
30 20
20 2
2 25
25 8
8 17
17 13
13 10
10 3
3 9

## output

4500
((M1 M2) M3)
7000
(M1 M2)
15125
((M1 (M2 M3)) ((M4 M5) M6))
48278
(M1 (M2 (M3 (M4 (M5 (M6 (M7 (M8 (M9 (M10 ((M11 (M12 (M13 (M14 (M15 (M16 (M17 (M18 (M19 (M20 (M21 (M22 (M23 (M24 (M25 (M26 (M27 (M28 (M29 (M30 (M31 (M32 (M33 (M34 (M35 (M36 M37)))))))))))))))))))))))))) (((((((((((((M38 M39) M40) M41) M42) M43) M44) M45) M46) M47) M48) M49) (M50 (M51 M52))) ((M53 M54) (((((((((((((((((((((((((((M55 M56) M57) M58) M59) M60) M61) M62) M63) M64) M65) M66) M67) M68) M69) M70) M71) M72) M73) M74) M75) M76) M77) M78) M79) M80) (M81 (M82 (M83 (M84 (M85 (M86 (M87 (M88 (M89 M90)))))))))) (((((((((M91 M92) M93) M94) M95) M96) M97) M98) M99) M100)))))))))))))))
118037
((M1 (M2 (M3 (M4 (M5 (M6 (M7 (M8 (M9 (M10 (M11 (M12 M13)))))))))))) ((((((((((((M14 M15) M16) M17) M18) M19) M20) M21) M22) (M23 (M24 (M25 (M26 (M27 (M28 (M29 (M30 (M31 M32)))))))))) ((M33 ((M34 M35) (M36 (M37 (M38 (M39 (M40 (M41 (M42 ((M43 M44) (M45 (M46 (M47 (M48 (M49 (M50 (M51 (M52 (M53 (M54 (M55 (M56 (M57 (M58 (M59 (M60 (M61 (M62 (M63 (M64 M65)))))))))))))))))))))))))))))) ((((((((((((((((M66 M67) M68) M69) M70) M71) M72) M73) M74) M75) M76) M77) M78) M79) M80) (M81 (M82 (M83 (M84 (M85 (M86 (M87 (M88 (M89 (M90 (M91 (M92 (M93 (M94 (M95 (M96 (M97 (M98 (M99 (M100 (M101 (M102 (M103 (M104 (M105 (M106 (M107 (M108 (M109 M110)))))))))))))))))))))))))))))) (((((((((M111 M112) M113) M114) M115) M116) M117) M118) M119) (((((((((M120 M121) M122) M123) M124) M125) M126) M127) (M128 (M129 (M130 (M131 (M132 (M133 (M134 (M135 (M136 (M137 (M138 (M139 (M140 (M141 (M142 (M143 (M144 (M145 (M146 (M147 (M148 (M149 (M150 (M151 (M152 (M153 (M154 (M155 (M156 (M157 (M158 M159)))))))))))))))))))))))))))))))) (((M160 M161) (M162 (M163 (M164 (M165 (M166 (M167 (M168 (M169 (M170 (M171 (M172 M173)))))))))))) (((((((((((((M174 M175) M176) M177) M178) M179) M180) M181) M182) M183) M184) M185) (M186 M187)) (((((((((M188 M189) M190) M191) M192) M193) M194) M195) (M196 (M197 (M198 (M199 (M200 (M201 (M202 (M203 M204))))))))) (((((((M205 M206) M207) M208) M209) M210) (M211 (M212 (M213 (M214 (M215 (M216 (M217 (M218 (M219 M220)))))))))) (((M221 M222) M223) (((((((((((((M224 M225) M226) M227) M228) M229) M230) M231) M232) M233) M234) M235) M236) (M237 (M238 (M239 (M240 (M241 (M242 M243))))))))))))))))) (((((M244 M245) M246) M247) M248) M249)) M250))

## vb.net

Module Module1

    Class Matrix
        Public Row, Col As Integer
        Public Sub New(ByVal row As Integer, ByVal col As Integer)
            Me.Row = row
            Me.Col = col
        End Sub
    End Class
    Class Node
        Public Matrix As Matrix
        Public Value As Integer
        Public Prev() As Integer
        Public Sub New(ByVal matrix As Matrix, Optional ByVal value As Integer = 0, Optional ByVal prev() As Integer = Nothing)
            Me.Matrix = matrix
            Me.Value = value
            Me.Prev = Prev
        End Sub
    End Class

    Sub Main()
        While True
            Dim Input As String = Console.ReadLine()
            If Input Is Nothing Then Exit While

            Dim LineCount As Integer = Input

            Dim DP(LineCount, LineCount) As Node

            ' init dp
            For i = 1 To LineCount
                Dim Data() As String = Console.ReadLine().Split(" ")
                Dim Matrix As New Matrix(Data(0), Data(1))
                DP(i, i) = New Node(Matrix)
            Next

            ' fill dp
            For i = 0 To LineCount - 1
                For j = 1 To LineCount - i - 1
                    Dim k As Integer = j + i + 1

                    Dim Minimum As Node = Nothing
                    For l = 0 To i
                        Dim PrevValue As Integer = DP(j, j + l).Value + DP(j + l + 1, k).Value
                        Dim Value As Integer = PrevValue + DP(j, j + l).Matrix.Row * DP(j, j + l).Matrix.Col * DP(j + l + 1, k).Matrix.Col
                        If Minimum Is Nothing OrElse Minimum.Value > Value Then
                            Minimum = New Node(New Matrix(DP(j, j + l).Matrix.Row, DP(j + l + 1, k).Matrix.Col), Value, {j, j + l, j + l + 1, k})
                        End If
                    Next

                    DP(j, k) = Minimum
                Next
            Next

            ' get solution
            Dim Output As String = GetResult(DP, 1, LineCount)

            Console.WriteLine(DP(1, LineCount).Value.ToString)
            Console.WriteLine(Output)
        End While
    End Sub

    Function GetResult(ByVal dp(,) As Node, ByVal i As Integer, ByVal j As Integer)
        If i = j Then Return "M" & i
        Dim Prev() As Integer = dp(i, j).Prev
        Dim Output As String = ""
        Output &= "(" & GetResult(dp, Prev(0), Prev(1)) & " "
        Output &= GetResult(dp, Prev(2), Prev(3)) & ")"
        Return Output
    End Function

End Module

## python

import sys


def get_result(dp, i, j):
    if i == j:
        return 'M' + str(i)

    prev = dp[i][j]['prev']
    output = ''
    output += '(' + get_result(dp, prev[0], prev[1]) + ' '
    output += get_result(dp, prev[2], prev[3]) + ')'
    return output

stdin = sys.stdin.read().splitlines()
while len(stdin) > 0:
    n = int(stdin.pop(0))
    dp = [{} for i in range(n+1)]

    for i in range(1, n+1):
        data = stdin.pop(0).split(' ')
        dp[i][i] = {
            'row': int(data[0]),
            'col': int(data[1]),
            'value': 0,
            'prev': ''
        }

    for i in range(0, n):
        for j in range(1, n-i):
            k = j + i + 1
            minimum = None

            for l in range(i+1):
                prev_value = dp[j][j+l]['value'] + dp[j+l+1][k]['value']
                value = prev_value + dp[j][j+l]['row'] * dp[j][j+l]['col'] * dp[j+l+1][k]['col']
                if minimum is None or minimum['value'] > value:
                    minimum = {
                        'row': dp[j][j+l]['row'],
                        'col': dp[j+l+1][k]['col'],
                        'value': value,
                        'prev': [j, j + l, j + l + 1, k]
                    }

            dp[j][k] = minimum


    output = get_result(dp, 1, n)
    print(dp[1][n]['value'])
    print(output)

---

# 四則運算
:::info
題意是輸入一個字串譬如2 * ( 3 + 4 ) * 5，
根據先乘除後加減及() 優先的運算規則，
把字串代表的值算出來(譬如說2 * ( 3 + 4 ) * 5 = 70)
(字串可能包含%(取餘數)，取餘數的運算優先順序與乘除同等級)
首先讀到一個字串，先把它轉換從infix表達式轉換成postfix，
再透過之前計算postfix表達式的算法，即可解開。
資結經典題目，
:::

<!---
https://ithelp.ithome.com.tw/articles/10231419

類似題目
leetcode- 224. Basic Calculator
leetcode- 227. Basic Calculator II
--->

#### Input
輸入一個字串，其中包含運算元及運算子，為了方便讀取，所有的運算子及運算元均以空格區隔。

運算元為 0 ~$2^{31}-1$ 的整數
運算子則包含 + - * / % 及 ( )

運算時請注意先乘除後加減及() 優先運算的計算規則

3+2*2
(1+(4+5+2)-3)+(6+8)
3+5 / 2

#### Output
輸出結果。為了避免小數點誤差，所有的運算過程都不會產生小數點，可以放心使用整數進行運算

7
23
5

#### Answer

import sys
for s in sys.stdin:
    print(eval(s.replace("/", "//")))

# 以1970-01-01開始的總天數
:::info
以1970-01-01開始的總天數為0，對應到的日期為 '1970-01-01'
以1970-01-01開始的總天數為1，對應到的日期為 '1970-01-02'
以1970-01-01開始的總天數為18039，對應到的日期為 '2019-05-23'
以1970-01-01開始的總天數為18405，對應到的日期為 '2020-05-23'
:::

:::danger
在Linux和Mac正常，在Windows無法跑，會出現OverflowError錯誤訊息

Traceback (most recent call last):
  File "time.py", line 6, in <module>
    end_sec2 = time.mktime(time.strptime(end_date,'%Y-%m-%d')) + date_time * (24*60*60)
OverflowError: mktime argument out of range

:::
#### Answer

import time
import datetime

date_time = 0
end_date = '1970-01-01'
end_sec2 = time.mktime(time.strptime(end_date,'%Y-%m-%d')) + date_time * (24*60*60)
print(time.strftime("%Y-%m-%d", time.localtime(end_sec2)) )

---

### 矩陣鏈乘積
:::info
矩陣鏈乘積（英語：Matrix chain multiplication，或Matrix Chain Ordering Problem，MCOP）是可用動態規劃解決的最佳化問題。給定一序列矩陣，期望求出相乘這些矩陣的最有效方法。此問題並不是真的去執行其乘法，而只是決定執行乘法的順序而已。

因為矩陣乘法具有結合律，所有其運算順序有很多種選擇。換句話說，不論如何括號其乘積，最後結果都會是一樣的。例如，若有四個矩陣$A$、$B$、$C$和$D$，將可以有：

$ABCD=(AB)(CD)=A(BCD)=A(BC)D= \dots$
但括號其乘積的順序是會影響到需計算乘積所需簡單算術運算的數目，即其效率。例如，設$A$為一$10\times 30$矩陣，$B$為$30\times 5$矩陣與$C$為$5\times 60$矩陣，則：

$(AB)C$有$(10\times 30\times 5)+(10\times 5\times 60)=1500+3000=4500$個運算

$A(BC)$有$(30\times 5\times 60)+(10\times 30\times 60)=9000+18000=27000$個運算

明顯地，第一種方式要有效多了。既然已確認過此問題了，那要如何決定$n$個矩陣相乘的最佳順序呢？可以比較每一順序的運算量（使用蠻力），但這將需要時間$O(2^n)$，是一種非常慢且對大$n$不實在的方法。那解決方法，如我們將看到的，是將問題分成一套相關的子問題。以解答子問題一次而再使用其解答數次，即可以徹底地得出其所需時間。此一方法稱為動態規劃。
:::
https://zh.wikipedia.org/wiki/%E7%9F%A9%E9%99%A3%E9%8F%88%E4%B9%98%E7%A9%8D

<!---

#### Input

1 

#### Output

2

#### Answer

#include<iostream>
using namespace std;
const int INT_MAX=2147483647;
int const M=7;
void MATRIX_CHAIN_ORDER(int *p,int Length,int m[][M],int s[][M])
{
	int q,n=Length-1;
	for(int i=1;i<=n;i++) m[i][i]=0;
	for(int l=2;l<=n;l++) 	/* 矩陣鏈的長度 */
	{
		for(int i=1;i<=n-l+1;i++) 
		{
			int j=i+l-1;         /* 等價於 l=j-i+1 */
			m[i][j]=INT_MAX;
			for(int k=i;k<=j-1;k++)
			{
				q=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
				if(q<m[i][j])
				{
					m[i][j]=q;
					s[i][j]=k;
				}
			}
		}
	}
}
void PRINT_OPTIMAL_PARENS(int s[][M],int i,int j)
{
	if(i == j) cout<<"A"<<i;
	else
	{
		cout<<"(";
		PRINT_OPTIMAL_PARENS(s,i,s[i][j]);
		PRINT_OPTIMAL_PARENS(s,s[i][j]+1,j);
		cout<<")";
	}
}
int main()
{
   int p[M]={30,35,15,5,10,20,25};
   int m[M][M],s[M][M];
   MATRIX_CHAIN_ORDER(p,M,m,s);
   cout<<"當n=6時最優解為: \n"<<m[1][6];
   cout<<"\n括號化方案為：\n"; 
   PRINT_OPTIMAL_PARENS(s,1,6);
   return 0;
}

https://www.itread01.com/content/1549055189.html

--->