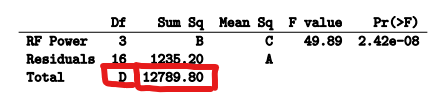
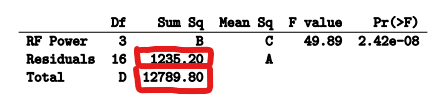
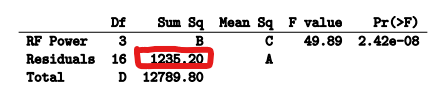
- ANOVA TABLE
- 
- # Columns
- Degrees of Freedom
- Sum of squares
- Mean of Squares
- F value / F statistic / F-ratio
- pr bullshit
- # Stats
- F ratio
- Found in column
- Critical value
- `qf(sig_value, df, df)`
- **IF THE F RATIO IS GREATER THAN THE CRIT VALUE, REJECT** $$H_0$$
- **IF PR_BULLSHIT IS LESS THAN SIG_VALUE, REJECT ** $$H_0$$
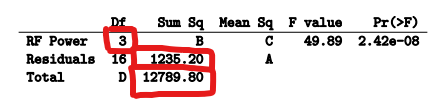
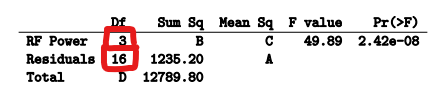
- # FINDING A, B, C, D
- A
- 
- 
- B
- 
- 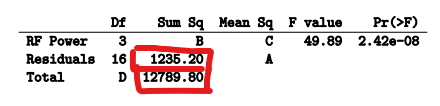
- C
- 
- 
- D
- 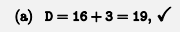
- 
- # TYPES OF MODELS
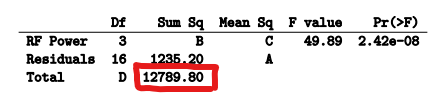
- REDUCED MODEL
- 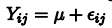
- STATS
- µ
- 
- 5 PLUS SAMPLE MEAN 1, 5 + SAMPLE MEAN 2, ETC ETC
- 
- $$σ^2$$
- 
- 
- RESIDUAL SUM OF SQUARES
- RIGHT HERE:
- 
- FULL MODEL
- 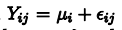
- STATS
- $$σ^2$$
- 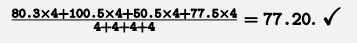
- 4 TIMES SAMPLE VARIANCE1, 4 TIMES SAMPLE VARIANCE 2, ETC
- 
- IT IS ALSO JUST "A"
- HERE IT IS AGAIN
- 
- RESIDUAL SUM OF SQUARES
- 
- SAME THING AS $$σ^2$$, BUT WITHOUT BEING DIVIDED BY 4 + 4+ ETC ETC
- 
- EXTRA SUM OF SQUARES
- THIS USES BOTH MODELS
- 
- 
- IF THIS IS GREATER THAN  YOU WANT TO USE THE FULL MODEL
- 3 TIMES "Critical value" TIMES RESIDUAL_SUMSQ
- RESIDUAL_SUMSQ CAN BE FOUND HERE
- 
-
- # DIAGNOSTIC CHECKING
- RESIDUALS
- OBSERVATION - FITTED VALUE
- RESIDUAL SUM OF SQUARES
- A MEASURE OF HOW WELL THE MODEL FITS THE DATA
- NORMALITY ASSUMPTION
- MAKE SURE THE DATA FITS A BELL CURVE
- USE THE HISTOGRAM AND QQ PLOT OF STANDARDISED RESIDUALS
- QQ PLOT
- IF THEY FIT ALONG THE LINE
- CONSTANT VARIANCE ASSUMPTION
- WHEN YOU PLOT THE INDIVIDUAL ERROR AGAINST PREDICTED VALUE, THE VARIANCE OF ERROR PREDICTED VALUE SHOULD BE CONSTANCT
- 
- STANDARDISED RESIDUALS
- IF GREATER THAN 2 OR LESS THAN -2 THEY ARE UNUSUAL OBSERVATIONS
- CORRELATED VALUES
-