###### tags: `softserve` `article`
# On the visualization of longitudinal data
## Introduction
If you are working on eHealthecare project you know that there are lots of longitudinal data. It means that we have many measurements of many features at different times. E.g., in clinical trials, we could have a thousand patients and each of them has measurements of blood pressure (BP), biochemistry, pulse, etc., measured weekly over a few months.
Most of the time you may find it useful to visualize your data for gaining insights or for presentation. And there are only a handful common ways to do it:
+ individual line trends
+ boxplots
+ violinplots
+ Sankey plots
All those methods have their flaws. Individual trends could be a mess, especially if you have a lot of patients, boxplots could be misleading and lose to violinplots almost in everything (e.g., [5 reasons you should use a violin graph](https://blog.bioturing.com/2018/05/16/5-reasons-you-should-use-a-violin-graph/)), violin plots do not show transitions between the states and sankey plot could be hard to read.
During our work with a Fortune 500 list company, we had a task to improve the treatment protocol for a certain chronic condition. At some point we recognized that client's data had four patient clusters instead of two, as they'd thought previously. The initial (pretty common) idea was to divide patients into groups of responding and non-responding to treatment. However, if we take a closer look from the different timescale it becomes clear that they also have patients who responded to therapy at first but failed at the end, and vice versa, those who failed at first but responded at the end.
It was a very valuable finding, which helped us a lot and it looked like an insight with a great business value, but we had to present it to the client in a transparent and understandable way. We were aware that a poor presentation of work results often leads to misunderstanding, client dissatisfaction, and reputational losses.
No one will believe in the significance of your discovery if you can not convey your message in a way that is clear and understandable to vis-a-vis. Moreover, the decision makers usually don’t have the time and/or expertise to dive into the tangled DS Jupyter notebooks or series of complicated plots for answers.
Thus, we had to choose the right way to plot our findings. We solved this problem creatively, the client was satisfied and now we want to share our experience. Because of NDA, we are not able to share original data or plots, so I’ll provide explanations based on small synthetically generated dataset, which is completely irrelevant to the original task but shares similar properties.
## Use case data generation
Consider the case: you have a thousand patients whose BP was measured 6 times at certain time points. You decide to group your BP results in 5 groups (1..5) by range, where 1 could represent the 'very low', and 5 'very high'. And now, you want to visualize results.
Here I generate a completely artificial dataset for illustrative purposes, with the very strange behavior of BP levels.
It looks like this (columns are patients, rows are points in time, cell values are BP group that Patient's BP fell into at a given time point):

:::spoiler *Code for data generation (click to show)*
```python
import pandas as pd
import numpy as np
import random
random.seed(999)
patients = 1000
time_points = 6
groups = [1, 2, 3, 4, 5]
# state distribution splits from initial 3 to 1 and 5
tmp = []
for _ in range(time_points):
x = np.array(random.choices(groups, k=patients, weights=[0.01, 0.48, 0.02, 0.48 ,0.01]))
tmp.append(x)
df0 = pd.DataFrame(tmp)
```
:::
## Why Vyshyvanka plot?
Let's plot generated data using each of three common methods:

:::spoiler *Common methods plot code (click to show)*
```python
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
def plot_common(df):
fig, axs = plt.subplots(3, 1, figsize=(12, 10), sharex=True)
fig.patch.set_facecolor('white')
fig.tight_layout(rect=[0, 0, 1, 0.96], h_pad=1.0, w_pad=0.94)
fig.suptitle(f'BP groups over time (n={df.shape[1]})', weight='bold')
# individual trends
for i in df:
axs[0].plot(df[i])
# boxplot and violin
ax = sns.boxplot(ax=axs[1], data=df.T, medianprops={'lw': 4})
ax = sns.violinplot(ax=axs[2], data=df.T, scale='count', inner='box')
for ax in axs:
_ = ax.set_yticks(np.unique(df0))
_ = ax.set_ylabel('BP group')
_ = axs[-1].set_xlabel('Time point')
plot_common(df0)
```
:::
<br />
We may see that individual trends are a mess, boxplots are not very informative and a violin plot shows us that patients are heavily distributed between 2nd and 4th groups and their distribution does not change significantly over time.
But this is simply not true, we created the dataset in a way where each patient has an equal chance to appear in the 2 or the 4 group at the next step. Will Sankey plot help us?

Well, a sort of (here `N_` numbers stands for BP group and `_M` numbers stands for certain time point, e.g. 3_2 is 3rd BP group at 2nd timepoint). We are able to see some transactions but the plot is too fiddly and obviously needs some tuning. You may find a separate chapter dedicated to Sankey plot problems on python below.
Meanwhile, compare it with a better way to visualize this:

I'll provide the code, but for now, let me describe the plot. It shows BP group transition over time. The line width and markers opacity (black dots) correlates with the number of patients. Here we can see that a majority of patients started in the 2 and the 4 groups and these groups have a stable amount of patients during the whole period of observation. But it also shows that there were 2 types of transitions with relatively equal probabilities: to remain in the initial group or switch between 2nd and 4th, with a small chance to switch to groups 1, 3, or 5. Here we do not see patients' individual pathways, rather the transition probability trends.
And this could be a pretty valuable insight. Also, it is a convenient plot to present and explain.
We have invented this plot almost by accident under the pressure of practical needs during our work with the real customer. Our Lviv teammates have named it "Vyshyvanka plot" due to similarity of appearance with the [national Ukrainian costume](https://en.wikipedia.org/wiki/Vyshyvanka) pattern.
Now, as promised, I'll share the code and a few more examples. In the remaining post I'll be plotting violin and vyshyvanka plots only because they are obviously superior to individual line trends and boxplots. Also, to make it more general, we will discontinue the BP groups example and just talk about state transitions over time.
:::spoiler *Vyshyvanka code (click to show)*
```python
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import itertools
def plot_vyshyvanka(df: pd.DataFrame, ax: plt.Axes,
coef_width=50, line_opacity=0.6, marker_opacity=0.1) -> (plt.Axes, int, np.ndarray):
"""
It will build the flow plot "Vyshyvanka": the transitions between possible states of
observations on the Y-axis over some time periods on the X-axis.
Line width and marker opacity correlate with the number of observations at a current point.
:param df: dataframe where columns are observations and rows are time points
:param ax: an instance of ``matplotlib.axes.Axes`` to plot on
:param coef_width: the bigger it, the thicker will be the lines
:param line_opacity: lines opacity
:param marker opacity: markers opacity
:return: (``matplotlib.axes.Axes``, number_of_observations_without_na, possible_states)
**Example:**
.. code-block:: python
import random
import pandas as pd
import matplotlib.pyplot as plt
obs_num = 1000
time_points = 8
states = [1, 2, 3, 4, 5]
tmp = []
for _ in range(time_points):
tmp.append(random.choices(states, k=obs_num,
weights=[0.05, 0.2 ,0.5, 0.2 ,0.05]))
df = pd.DataFrame(tmp)
fig, ax = plt.subplots(figsize=(15, 7))
fig.patch.set_facecolor('white')
ax, num, relevant_states = plot_vyshyvanka(df, ax)
_ = ax.set_yticks(relevant_states)
_ = ax.set_xlabel('Time points')
_ = ax.set_ylabel('States')
_ = ax.set_title(f'State transitions over time (n={num})')
"""
# drop observations with NA an count what left
df_plot = df.dropna(axis=1)
obs_num = len(df_plot.columns)
# iterate over time points using sliding window with length=2, stride=1
for row1, row2 in zip(itertools.islice(df_plot.iterrows(), 0, None, 1),
itertools.islice(df_plot.iterrows(), 1, None, 1)):
# get row idxs (from df.iterrows() output)
x1 = row1[0]
x2 = row2[0]
# get row values
tmp = pd.concat([row1[1], row2[1]], axis=1).to_numpy()
# count unique pairs was-now states
pairs, nums = np.unique(tmp, axis=0, return_counts=True)
# get all possible states
states = np.unique(pairs.flatten())
# calculate line widths for each pair (state transition)
# line width correlates with observations amount,
# where ``obs_num * coef_width`` is the maximum width
widths = nums / obs_num * coef_width
# add axis to widths in order to merge it with pairs for comfy iteration
for row in np.hstack([pairs, np.expand_dims(widths, axis=1)]):
y1, y2, w = row
# plot line
ax.plot([x1, x2], [y1, y2], linewidth=w, color='red', alpha=line_opacity, solid_capstyle='round')
# plot markers
# marker opacity correlates with observations amount
ax.plot(x1, y1, 'o', markersize=2, color='black', alpha=marker_opacity)
ax.plot(x2, y2, 'o', markersize=2, color='black', alpha=marker_opacity)
return ax, obs_num, states
```
:::
## Python problems with Sankey plot
There are not so many python plotting libs ([link1](https://mode.com/blog/python-data-visualization-libraries/), [link2](https://mode.com/blog/python-interactive-plot-libraries/)) and only a few that could do Sankey plots -- [matplotlib](https://matplotlib.org/api/sankey_api.html), [holoviews](https://holoviews.org/reference/elements/bokeh/Sankey.html) and [plotly](https://plotly.com/python/sankey-diagram/) (also there is a jupyter widget [ipysankeywidget](https://github.com/ricklupton/ipysankeywidget)). But only one lib could create beautiful enough Sankey plots -- plotly (through JS frontend).
:::spoiler *Here is the code for example Sankey plot (click to show)*
```python
import numpy as np
import pandas as pd
import plotly.graph_objects as go
import itertools
def prepare_data_for_sankey(df: pd.DataFrame) -> (np.ndarray, np.ndarray, np.ndarray, list):
""" Convert our data for sankey
We need next one dimensional vectors:
FROM, TO, HOW_MANY, NODE_LABLES (source, target, value, labels)
:return: ``(source, target, value, labels)``
"""
tmp = df.to_numpy()
time_points = tmp.shape[0]
source = []
target = []
value = []
# get groups range
groups = range(np.unique(df).min(), np.unique(df).max() + 1)
# generate lables -- all possible combinations of groups and time points
labels = [f'{g}_{t}' for g, t in itertools.product(groups, range(time_points))]
# all possible transitions betveen 5 BP groups
all_variants = np.array(list(itertools.product(groups, groups)))
# sliding widow for time points with size=2 and step_size=1
for i in range(time_points - 1):
pairs, counts = np.unique(tmp[i+0:i+2].T, axis=0, return_counts=True)
# check every possible transaction
for v in all_variants:
# check if we have this theoretical variant in our real pairs
mask = (pairs == v).all(axis=1)
if mask.sum() == 1:
# get HOW_MANY from counts
value.append(counts[mask][0])
else:
value.append(0)
# i for BP group 'now'
source.append(labels.index(f'{v[0]}_{i}'))
# i+1 for BP group 'in future'
target.append(labels.index(f'{v[1]}_{i+1}'))
return source, target, value, labels
def plot_sankey(source: np.ndarray, target: np.ndarray,
value: np.ndarray, labels: list) -> go.Figure:
""" Based on <https://plotly.com/python/sankey-diagram/>
source and target are indices correspond to labels
"""
fig = go.Figure(data=[go.Sankey(
arrangement = "perpendicular",
node = dict(
pad = 15,
thickness = 20,
line = dict(color = "black", width = 0.5),
label = labels,
color = "red",
),
link = dict(
source = source,
target = target,
value = value
))])
return fig
def convert_and_plot_sankey(df: pd.DataFrame, order=False) -> go.Figure:
"Both above functions in one place + node ordering"
source, target, value, labels = prepare_data_for_sankey(df)
fig = plot_sankey(source, target, value, labels)
if order:
groups = len(np.unique(df))
time_points = df.shape[0]
# Xs
pre_x = np.expand_dims(np.linspace(1e-09, 1, time_points), axis=1)
fig.data[0].node.x = pre_x.repeat(groups, axis=1).T.flatten()
# Ys
pre_y = np.expand_dims(np.linspace(1e-09, 1, groups), axis=1)
fig.data[0].node.y = pre_y.repeat(time_points, axis=1).flatten()
# make lables smaller
fig.update_traces(textfont={'size': 10})
# remove big margins
fig.update_layout(margin=dict(l=25, r=25, b=50, t=50, pad=0))
return fig
```
:::
```python
fig = convert_and_plot_sankey(df0)
fig.show()
```

To make it more intuitive we must force-order our BP groups like on Vyshyvanka plot, thus we will able to keep track of group transitions much more easily:
```python
### order nodes on sankey plot
# Plot same states on the same line (as on vyshyvanka plot)
fig = convert_and_plot_sankey(df0, order=True)
fig.show()
```
:::spoiler *Ordering code explanation (click to show)*
```python
""" We need to set x and y normalized coordinates (0..1) for each node.
And they can't be exactly 0.
We just will try to distribute them evenly, but in certain order,
where all timepoints of single BP group must be on one line.
"""
time_points = 6
groups = 5
#We have nodes in that order
fig.data[0].node.label
>>>[1_0, 1_1, 1_2, 1_3, 1_4, 1_5,
2_0, 2_1, 2_2, 2_3, 2_4, 2_5,
3_0, 3_1, 3_2, 3_3, 3_4, 3_5,
4_0, 4_1, 4_2, 4_3, 4_4, 4_5,
5_0, 5_1, 5_2, 5_3, 5_4, 5_5]
# Xs: each group of (1_n..5_n) labels should be aligned vertically
np.expand_dims(np.linspace(0, 1, time_points), axis=1).repeat(groups, axis=1).T.flatten()
>>>array([0. , 0.2, 0.4, 0.6, 0.8, 1. ,
0. , 0.2, 0.4, 0.6, 0.8, 1. ,
0. , 0.2, 0.4, 0.6, 0.8, 1. ,
0. , 0.2, 0.4, 0.6, 0.8, 1. ,
0. , 0.2, 0.4, 0.6, 0.8, 1. ])
# Ys: each group of (n_1 .. n_5) labels should be aligned horizontally
np.expand_dims(np.linspace(1e-09, 1, groups), axis=1).repeat(time_points, axis=1).flatten()
>>>array([0. , 0. , 0. , 0. , 0. , 0.,
0.25, 0.25, 0.25, 0.25, 0.25, 0.25,
0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 ,
0.75, 0.75, 0.75, 0.75, 0.75, 0.75,
1. , 1. , 1. , 1. , 1. , 1. ])
```
:::
</br>

Despite that on this example everything seems OK, plotly has a lot of problems with changing default nodes order, which makes it hard to use it on most data (see [examples](https://gitlab.com/banderlog/vyshyvanka_plot_article/-/blob/master/sankey_plot.ipynb)).
Consider these github issues (especially the last one):
+ [FR: Add textposition property for Sankey plot's node labels](https://github.com/plotly/plotly.py/issues/3004)
+ [Sankey node x and y positions require both variables set to reflect in chart](https://github.com/plotly/plotly.py/issues/1732)
+ [Sankey node x and y positions could not be equal to 0 or np.nan](https://github.com/plotly/plotly.py/issues/3002)
+ [Sankey node x and y positions ignored if node is empty](https://github.com/plotly/plotly.py/issues/3003)
## Examples
You may find all relevant Jupyter notebooks with all code from this post [here](https://gitlab.com/banderlog/vyshyvanka_plot_article).
:::spoiler *Wrapper plot function which we will use in further examples (click to show)*
```python
import matplotlib.pyplot as plt
import seaborn as sns
def plot_violins_and_vyshyvanka(df):
fig, axs = plt.subplots(2, 1, figsize=(10, 10), sharex=True)
fig.patch.set_facecolor('white')
fig.tight_layout(rect=[0, 0, 1, 0.96], h_pad=1.0, w_pad=0.94)
ax = sns.violinplot(ax=axs[0], data=df.T, scale='count', inner='box')
ax, obs_num, states = plot_vyshyvanka(df, axs[1])
_ = axs[1].set_xlabel('Time points')
for ax in axs:
_ = ax.set_yticks(states)
_ = ax.set_ylabel('States')
fig.suptitle(f'State transitions over time (n={obs_num})', weight='bold')
```
:::
### State distribution changes with mode of 1->5 transition
:::spoiler *Data geneation for this example (click to show)*
```python
# state distribution changes from 1 to 5 mostly
random.seed(999)
obs_num = 1000
time_points = 12
states = [1, 2, 3, 4, 5]
tmp = []
x = np.array(np.array(random.choices(states, k=obs_num, weights=[0.64, 0.2, 0.1, 0.05, 0.01])))
tmp.append(x)
for _ in range(time_points - 1):
x = x + np.array(random.choices([-1, 0, 1], k=obs_num, weights=[0.1, 0.45, 0.45]))
x = np.clip(x, 1, 5)
tmp.append(x)
df2 = pd.DataFrame(tmp)
```
:::


### State distribution changes, bi-modal 1->5 and 5->1 transitions
:::spoiler *Data geneation for this example (click to show)*
```python
# state distribution changes from 1 to 5 and back to 1
random.seed(999)
obs_num = 1000
states = [1, 2, 3, 4, 5]
tmp = []
x = np.array(np.array(random.choices(states, k=obs_num, weights=[0.64, 0.2 ,0.1, 0.05 ,0.01])))
tmp.append(x)
for _ in range(5):
x = x + np.array(random.choices([-1, 0, 1], k=obs_num, weights=[0.05, 0.45, 0.5]))
x = np.clip(x, 1, 5)
tmp.append(x)
x = x + np.array(random.choices([-1, 0, 1], k=obs_num, weights=[0.05, 0.9, 0.05]))
x = np.clip(x, 1, 5)
tmp.append(x)
for _ in range(5):
x = x + np.array(random.choices([-1, 0, 1], k=obs_num, weights=[0.55, 0.4, 0.05]))
x = np.clip(x, 1, 5)
tmp.append(x)
df3 = pd.DataFrame(tmp)
```
:::


### State distribution splits from initial 3 flowing to either 1 or 5 ultimately
:::spoiler *Data geneation for this example (click to show)*
```python
# state distribution splits from initial 3 to 1 or 5 mostly
random.seed(999)
obs_num = 1000
time_points = 12
states = [1, 2, 3, 4, 5]
# state distribution splits from initial 3 to 1 and 5
tmp = []
x = np.array(random.choices(states, k=obs_num, weights=[0, 0, 1, 0 ,0]))
tmp.append(x)
for _ in range(time_points - 1):
x = x + np.array([random.choices([-1, 0, 1], k=int(obs_num/2), weights=[0.02, 0.48, 0.5]),
random.choices([-1, 0, 1], k=int(obs_num/2), weights=[0.5, 0.48, 0.02])]).ravel()
x = np.clip(x, 1, 5)
tmp.append(x)
df4 = pd.DataFrame(tmp)
```
:::


## Interactive Vyshyvanka plot
In rare cases, you might want to make it interactive so that to be able to know exact number and percent of transitioned states by clicking on a line. Also, interactive mode allows for finding optimal values for opacity and line widths. For this, we provide you with the code below. Keep in mind, that it will work in Jupyter notebook or a Jupyter-lab upon installation of [mplcursors](https://mplcursors.readthedocs.io/en/stable/) and [ipywidgets](https://github.com/jupyter-widgets/ipywidgets/blob/master/docs/source/user_install.md) (be careful with virtualenv)
:::spoiler *Interactive Vyshyvanka plot code (click to show)*
```python
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.lines import Line2D
import random
import itertools
import mplcursors
import ipywidgets as widgets
from ipywidgets import interact
from matplotlib.legend import Legend
from typing import List
%matplotlib widget
###### Dataset generation
# for reproducibility
random.seed(999)
# create dataset
patients = 1000
time_points = 6
groups = [1, 2, 3, 4, 5]
tmp = []
for _ in range(time_points -1 ):
x = np.array(random.choices(groups, k=patients, weights=[0.01, 0.48, 0.02, 0.48 ,0.01]))
tmp.append(x)
df = pd.DataFrame(tmp)
###### Static part
## Plot
coef_width = 50
fig, ax = plt.subplots(figsize=(9, 4))
fig.patch.set_facecolor('white')
ax, num, relevant_states = plot_vyshyvanka(df, ax, coef_width=coef_width)
_ = ax.set_yticks(relevant_states)
_ = ax.set_xlabel('Time points')
_ = ax.set_ylabel('States')
_ = ax.set_title(f'State transitions over time (n={num})')
## Generate legend
# create lines which represent different percent of observations (number of observations)
steps = ([0.25, 0.1, 0.05, 0.01])
lines = [Line2D([0], [0], color='red', alpha=0.6, solid_capstyle='round', lw=(coef_width * i)) for i in steps]
l_labels = [f'{i*100:.0f}% ({i*num:.0f})' for i in steps]
legend = ax.legend(lines, l_labels, loc='upper left', borderpad=0.8, handlelength=1, handletextpad=1)
###### Interactive part
## Interactive sliders for line opacity and width change
class Foo:
def __init__(self, ax: plt.Axes, legend: Legend):
""" This is the only known way to avoid global variables
with ipwidgets updates on interaction
"""
self.ax = ax
self.legend = legend
def update(self, width_coeff: int, line_opacity: float,
orig_w: List[float], orig_l_w: List[float]) -> None:
""" Will set new width and opacity for every line
on legend and plot
:param width_coeff: this affects line width
:param line_opacity: this affects line opacity
:param orig_w: previous line widths on Axes
:param orig_l_w: previous line widths on Legend
"""
# set new width and opacity for Axes lines
for line, w in zip(self.ax.get_lines(), orig_w):
line.set_lw(w * width_coeff)
line.set_alpha(line_opacity)
# set new width and opacity for Legend lines
for line, w in zip(self.legend.get_lines(), orig_l_w):
line.set_lw(w * width_coeff)
line.set_alpha(line_opacity)
# get current width for lines on plot and on legend
orig_widths = [line.get_lw() for line in ax.get_lines()]
orig_l_w = [line.get_lw() for line in legend.get_lines()]
# plot actual sliders
updater = Foo(ax, legend)
interact(updater.update,
width_coeff=widgets.FloatSlider(min=0, max=2, step=0.1, value=1),
line_opacity=widgets.FloatSlider(min=0, max=1, step=0.05, value=0.4),
orig_w=widgets.fixed(orig_widths),
orig_l_w=widgets.fixed(orig_l_w))
## Interactive annotation
# set label "percent_of_observations / number_of_observations" for each line
for line, w in zip(ax.get_lines(), orig_widths):
tmp = w / coef_width
line.set_label(f'{tmp * 100:.1f}% / {tmp * num:.0f}')
# on LB (on line) it will show annotation
# on RB (on annotation) it will hide it
mplcursors.cursor().connect("add", lambda sel: sel.annotation.set_text(sel.artist.get_label()));
```
:::
</br>
You should get something like this:
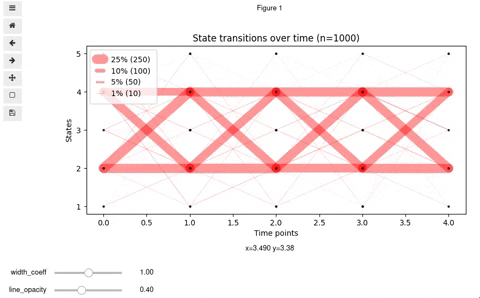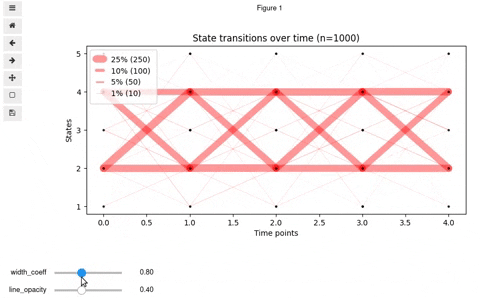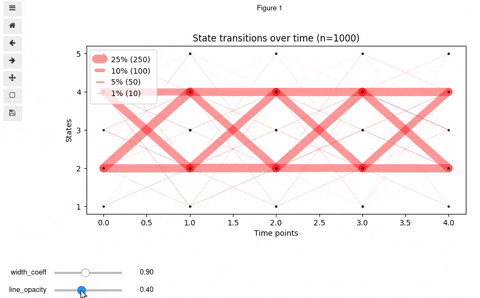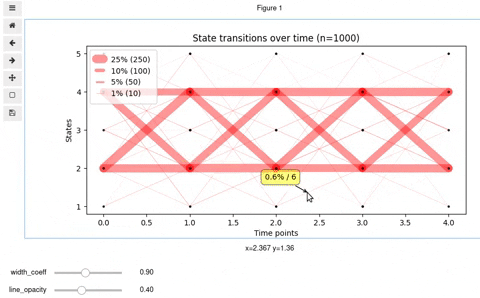
We hope some of you find the Vyshyvanka plot useful :)