## 為何要用到 DFS/BFS
在遍歷任何圖時，由於圖不像是線性結構這樣方便用 index 得知兩個節點之間的關係
圖上 DFS/BFS 就是為了能有系統性地遍歷圖所研究出來的演算法

## DFS(深度優先搜尋)
DFS 可以大致拆分成四個步驟
1. 決定起點(起始目前點)
2. 找一個與目前點連通並且未被走過的點 $A$
3. 將點 $A$ 設為目前點
4. 重複 $2,\ 3$ 直到所有點都被走過了

從上述的四個步驟可以發現深度優先的概念就是找一條路走到死，然後不斷重複
如果用只有左轉右轉直行三個可能選項的迷宮當作圖來看，每個叉路口都是節點
DFS 在這個例子當中可以分成幾個操作
1. 選擇往右走
2. 選擇往中走
3. 選擇往左走
4. 回到上一個節點

所以在這個例子當中，我們可以先重複 $1$ 直到死路，做 $4$ 之後選擇 $2$ 到下一個節點
在這個新節點在重複選 $1$，做 $4$ 之後選擇 $2$ 到下一個節點...
其實整體的策略就是一句話 "當一個節點往某個方向的延伸的所有節點都被走完，就選擇一個新的方向"

在實際操作上會用遞迴(較多)或是 stack (較少)去做 DFS 的操作
因為一直往前走直到死路 `return ;`，跟回到上一個分岔處，就跟遞迴一樣概念
之前有看過很好的舉例，DFS 很像遊戲存檔，但是這裡的存檔是為了跑過遊戲所有可能的劇情
所以不會覆蓋存檔，只在存檔之後的劇情都確定跑過了，才會把該存檔刪除，然後回到更早的存檔
而一直往前走的特性則是跟 stack 一樣，因為 stack 是後進先出，所以最新發現的路會最先被走
如下圖，每個點就是一個分岔，下圖就是要從 $S$ 走到 $E$

#include<bits/stdc++.h>
using namespace std ;
typedef vector<vector<int>> VVi ;

bool gone[1005] = {} ; // 初始化為 false
void dfs(int now, VVi &G) {
    cout << now << ' ' ; // 目前節點
    gone[now] = true ;
    
    for (int &it: G[now]) { // 與目前節點相連的節點
        if (!gone[it]) dfs(it, G) ;
    }
    return ;
}

int main() {
    ios::sync_with_stdio(0), cin.tie(0) ;
    
    int v, e ;
    cin >> v >> e ; // v 個節點 e 個邊
    
    VVi G(v) ; // Adjacency List
    for (int i=0;i<e;i++) { // 無向邊
        int a, b ;
        cin >> a >> b ;
        G[a].push_back(b) ;
        G[b].push_back(a) ;
    }
    
    int now = 0 ; // 起點
    dfs(now, G) ; // dfs

    return 0 ;
}

以上程式碼片段大概要注意的地方有四點
第一是我的點是從 $0$ 開始，所以 vector 的空間是開剛好
如果點從 $1$ 開始可以把 vector 多開一格，或是把題目給的編號-1
第二是新節點先選哪個邊是根據邊存入的順序決定的
如果要更改順序，可以自行用 for 迴圈去調整或是照編號大小排序
第三是二維 vector 傳入 function 要注意的事情
上面這種寫法是我認為最方便的寫法，不需要考慮指標控制
也可以做到修改正確的二維 vector 跟節省資源
直接把 vector 放在 global 也可以
第四是用 for 迴圈跑 vector 有很多方式，上方也是用最方便的方式
不過要注意如果邊的型態不同就要考慮 it 的資料型態

### 例題-CSES Building Roads
[題目連結](https://cses.fi/problemset/task/1666) (例題有稍加修改，所以跟連結內題目不太一樣)
有 $n$ 個城市，城市之間有 $m$ 個雙向道路，其中第 $i$ 條道路連接 $a_i,\ b_i$
求之間還需要再建造幾條道路才可以讓每一座城市都有道路可以互相連通
並且輸出需要連接的城市，兩連結的城市需要找最小的編號
第一行先輸入 $n\ m$，第二行開始有 $m$ 條道路
範例輸入 :
4 2
1 2
3 4

範例輸出 :
1
1 3

// 範例解釋 : 因為整張圖有兩個連通區塊$(\{1,2\},\{3,4\})$，從兩個區塊找最小編號 $1,\ 3$ 連接

解題思路 :
這題因為用到連通塊之間的連結，所以可以用[並查集](https://hackmd.io/@apcser/HJjkpKoCn)的方式
不過現在主要講 DFS，所以先不展開講，從題目來看，不管有多少區塊
只要有任何區塊要跟包含 $1$ 的區塊連結(蓋路)，就必須連結 $\{1,v\}$
所以可以先從 $1$ 開始進行 DFS，找到所有跟 $1$ 連通的點後
就能從 $2$ 開始枚舉所有點，只要找到還沒走過的點 $V$，就將 $V$ 跟 $1$ 做連接
並且找到跟 $V$ 連通的所有點，不斷重複到最後一個點就可以了
(注意原本題目沒有指定兩聯通方塊的連接編號，所以下方程式提交也能過)

#include<bits/stdc++.h>
using namespace std ;
typedef vector<vector<int>> VVi ;
typedef pair<int, int> Pii ;
#define FF first
#define SS second

bool gone[1005] = {} ; // 初始化為 false
void dfs(int now, VVi &G) {
    gone[now] = true ;

    for (int &it: G[now]) { // 與目前節點相連的節點
        if (!gone[it]) dfs(it, G) ;
    }
    return ;
}

int main() {
    ios::sync_with_stdio(0), cin.tie(0) ;

    int n, m ;
    cin >> n >> m ; // n 個節點 m 個邊

    VVi G(n+1) ; // Adjacency List
    for (int i=0;i<m;i++) { // 無向邊
        int a, b ;
        cin >> a >> b ;
        G[a].push_back(b) ;
        G[b].push_back(a) ;
    }

    int ans = 0 ; // 答案數量
    vector<Pii> ansE ;
    dfs(1, G) ; // 從 1 開始進行 dfs

    for (int i=2;i<=n;i++) { // 從第二個點開始找未連通的點
        if (!gone[i]) { // 未連接
            dfs(i, G) ; // 連接 i 後
            // 所有原本與 i 連通的節點都與 1 連通了

            // 答案數量+1
            ans++ ;
            ansE.push_back({1, i}) ;
        }
    }

    // 輸出答案
    cout << ans << '\n' ;
    for (Pii &it: ansE)
        cout << it.FF << ' ' << it.SS << '\n' ;

    return 0 ;
}

## BFS(廣度優先搜尋)
BFS 可以大致拆分成四個步驟
1. 決定起點(起始目前點)
2. 找到所有與目前點連通並且未被走過的點 $A$
3. 將所有點 $A$ 放入 queue 等著處理
4. 重複 $2,\ 3$ 直到所有點都被走過了

從上述的四個步驟可以發現廣度優先的概念就是先找到所有能走的路，然後不斷重複
跟 DFS 不同的概念，BFS 會像是淹水一樣，會同時處理**與原點等距**的所有路
而這裡的等距是點 $A$ 跟點 $B$ 之間最短由幾個邊連接，而非點之間邊權重相加
需要注意的地方除了用法的不同之外，還有點是否走過的判斷時機
因為 BFS 是一次加入很多點，所以不能再碰到某點時才將某點設成走過的狀態
為了避免重複將同一點放入 queue，我們要在**加入點時就設成走過**
使用 queue 的原因是 BFS 要優先處理同一層(與原點等距)的點，所以先丟進去的點先處理
也是利用 queue 先進先出的特性才能達到最高的效率
如下圖同時亮紅色的代表他們都是同一個層數

#include<bits/stdc++.h>
using namespace std ;
typedef vector<vector<int>> VVi ;

int main() {
    ios::sync_with_stdio(0), cin.tie(0) ;
    
    int n, m ;
    cin >> n >> m ;
    
    VVi G(n) ;
    for (int i=0;i<m;i++) {
        int a, b ;
        cin >> a >> b ;
        
        G[a].push_back(b) ;
        G[b].push_back(a) ;
    }
    
    vector<int> gone(n, false) ; // 節點 i 是否走過
    queue<int> que ;
    q.push(0) ; // 從節點 0 開始
    gone[0] = true ;
    
    while (!que.empty()) {
        int now = que.front() ; // 目前節點
        que.pop() ;
        
        cout << now << ' ' ;
        for (int &it: G[now]) { // 與目前節點相連的點
            if (!gone[it]) {
                que.push(it) ;
                gone[it] = true ;
            }
        }
        
    }
    return 0 ;
}

以上程式碼片段要注意的地方只有 gone 的更新
因為不需要考慮傳 vector 入 function 的問題
如果沒有將 gone 提前更新，會導致複雜度過大，舉個例子就能明白
如果點 $A$ 連接到 $6$ 個點，假如現在因為 gone 的更新失誤
導致 queue 有 $20$ 個點 $A$，queue 會加入 $6\times20$ 個點
如此往復，queue 一定可以清空，但是有很多點都被重複處理了

## 複雜度
以下都是以 Adjacency List 儲存圖，因為在各種題目中較常使用
DFS/BFS 的時間複雜度都是 $O(V+E)$，空間複雜度是 $O(V)$

## 差異與選擇
兩者在演算法上的差異就是一個是走到底再回頭，一個是一步步處理同距的節點
DFS 在節點分支較少或討論深度問題時比較適合，同時記憶體需求通常比 BFS 低
不過在存在深度很大或有循環結構的情況下，需要特別注意 stack overflow
BFS 則可避免這種問題，但因為逐層訪問，如果圖的結構廣度非常大(分支多)，記憶體消耗也會增加
## 實際應用
除了基礎的使用之外，DFS/BFS 配合圖或樹會有更進一步的演算法，比如拓樸排序，DFS 樹等等
但是這裡不會介紹，因為比較適合跟其他主題一起講述

## 其他例題
### 例題-ZJ a290. 新手訓練系列 ~ 圖論
[題目連結](https://zerojudge.tw/ShowProblem?problemid=a290)
給定多條單向路，問城市 $A$ 能否到城市 $B$，可以就輸出 "Yes!!!"，不行就輸出 "No!!!"，多筆測資輸入
每筆輸入第一行有兩個正整數 $N$ , $M$ ( $N \le 800$ , $M \le 10000$ )，代表有 $N$ 個城市 $M$ 條道路
接下來有 $M$ 行， 每行有 $2$ 個正整數 $a$ , ( $1 \le a$ , $b \le N$ )
代表有一條從 $a$ 城市到 $b$ 城市的單向道路
最後一行有兩個正整數 $A$ , $B$ ( $1 \le A$ , $B \le N$ )

範例輸入 :
7 9
7 4
2 5
7 5
3 7
2 1
2 2
2 4
4 4
4 7
4 7

範例輸出 :
Yes!!!

解析 :
這題只要存圖然後從點 $A$ 開始**遍歷整張圖**就可以了，至於用 DFS 或是 BFS 都可
存圖的方式基本上用 vector 存，因為用二維陣列的方式沒辦法有效的去找某點的所有邊
如果題目重複詢問次數拉高，則可以在輸入測資時對所有點先做處理，能較快速的去解決問題

#include<bits/stdc++.h>
using namespace std ;

bool gone[805] = {} ;

bool dfs(int now, vector<vector<int>> &G, int &b) {
    gone[now] = true ; // 走過了
    if (now == b) return true ; // 可以走到 b
    for (int &it: G[now]) {
        if (!gone[it] && dfs(it, G, b))
            return true ; // 可以走到 b
    }
    return false ; // 無路可走了
}

int main() {
    ios::sync_with_stdio(0), cin.tie(0) ;

    int n, m ;
    while (cin >> n >> m) {
        // 清除上一組測資
        vector<vector<int>> G(n+1) ;
        for (int i=0;i<=n;i++) gone[i] = false ;

        int a, b ;
        for (int i=0;i<m;i++) {
            cin >> a >> b ;
            G[a].push_back(b) ;
        }

        cin >> a >> b ;
        if (dfs(a, G, b)) // 可以走到
            cout << "Yes!!!\n" ;
        else
            cout << "No!!!\n" ;
    }

    return 0 ;
}

### 例題-ZJ b545. 1.蟲蟲鑽洞問題
[題目連結](https://zerojudge.tw/ShowProblem?problemid=b545)
生物學家要研究一種生活在木頭裡的蟲，主要式統計牠移動時鑽洞的行為模式
現在我們要寫出一個程式來分析資料庫裡牠在每塊木頭中移動過後留下來的洞，來紀錄牠鑽洞的合理路徑
資料庫裡每個留下來的數據都是由一個 MxN 的矩陣組成，已知蟲只會鑽一次洞，且可能會轉彎，但不會回頭
給定蟲鑽完洞的結果，且洞不會形成環，問蟲的起點、轉彎點、終點
並且起點取 $x,\ y$ 較小值(先看 $x$ 再看 $y$ )去回答

範例輸入 :
5 4
0\*\*\*0
0\*0\*0
\*\*0\*0
000\*\*

範例輸出 :
1 3
2 3
2 1
4 1
4 4
5 4

測資解釋 :
從 $(1,3)、(5,4)$ 進入才能透過轉彎走過全部的路，且 $(1,3)$ 較小

解析 :
觀察可以發現起點與終點上下左右四格中只有一格會是 "\*"
其餘點上下左右四格中會有兩格是 "\*"
所以用這個性質配合題目要求 $x$ 較小就可以找到起點
不過要注意這裡的 $x,y$ 會對應到的位置是 `A[y][x]`
然後再從起點做 BFS 就可以找到整個路徑
至於轉折點的判斷有許多方法，這裡提供兩個
1. 在 BFS 過程中判斷前後兩點方向，藉此判斷是否為轉折點
2. 將整段路徑記錄下來，在最後判斷前後兩點方向，判斷轉折點

以下的程式碼採取第一種作法

#include<bits/stdc++.h>
using namespace std ;
typedef pair<int, int> Pii ;
#define FF first
#define SS second

int main() {
    ios::sync_with_stdio(0), cin.tie(0) ;

    int mm[4][2] = {0,1, 0,-1, 1,0, -1,0} ; // 01 23

    int n, m ;
    cin >> m >> n ;

    vector<string> G(n) ;
    for (int i=0;i<n;i++)
        cin >> G[i] ;

    int a=-1, b=-1 ; // 起點座標
    for (int i=0;i<m && a<0;i++) { // 注意題目要求是 A[y][x]
        for (int j=0;j<n && a<0;j++) {
            if (G[j][i] == '*') {
                int cnt = 0 ;
                for (int k=0;k<4;k++) {
                    int nx = i+mm[k][0] ;
                    int ny = j+mm[k][1] ;
                    if (nx<m && nx>=0 && ny<n && ny>=0)
                        if (G[ny][nx] == '*')
                            cnt++ ;
                }
                if (cnt == 1)
                    a = j, b = i ;
            }
        }
    }

    vector<Pii> ans ;
    queue<Pii> que ;
    que.push({a, b}) ;
    ans.push_back({a, b}) ; // 起點
    G[a][b] = '.' ;

    while (!que.empty()) { // BFS
        Pii now = que.front() ;
        que.pop() ;

        int to1 = -1, to2 = -1 ; // 轉折點到旁邊"兩點"方向
        
        for (int i=0;i<4;i++) { // 找可走節點順便求 to1, to2
            int nx = now.FF+mm[i][0], ny = now.SS+mm[i][1] ;
            if (nx<n && nx>=0 && ny<m && ny>=0) {
                if (G[nx][ny] == '.')
                    to1 = i ;
                else if (G[nx][ny] == '*') {
                    to2 = i ;
                    G[nx][ny] = '.' ;
                    que.push({nx, ny}) ;

                }
            }
        }
        // 判斷轉折點
        if (to1 == 0 && (to2 == 2 || to2 == 3))
            ans.push_back(now) ;
        else if (to1 == 1 && (to2 == 2 || to2 == 3))
            ans.push_back(now) ;
        else if (to2 == 0 && (to1 == 2 || to1 == 3))
            ans.push_back(now) ;
        else if (to2 == 1 && (to1 == 2 || to1 == 3))
            ans.push_back(now) ;
        else if (to2 == -1) // 終點
            ans.push_back(now) ;
    }

    for (Pii &it: ans) // 最後記得轉回題目要求
        cout << it.SS+1 << ' ' << it.FF+1 << '\n' ;

    return 0 ;
}

不過這題挺有意思的，其實起點的找法可以先隨便找一個點，然後從這個點做 BFS 找到起終點
然後找出起點後再做 BFS/DFS，有點像是從樹上隨機點做兩次 BFS 找樹的直徑
也可以隨便找一個點 $N$，把儲存答案的方式改成用 deque，然後從 $N$ 前後兩點分別做 BFS
這樣看起來像做兩次 BFS，實際兩次 BFS 都跑不重複的節點，大約等於一次 BFS 跑全部節點
這個概念比較像從根往底下不同子節點找樹的直徑，這兩種方法的概念在[樹論](/B1Oi9pzkex)有提到
### 例題-ZJ c812. 1. 觀光景點
[題目連結](https://zerojudge.tw/ShowProblem?problemid=c812)
打卡公司為了促進城市觀光，發展一個可推薦前往觀光(打卡)的App
該公司選定了 $N$ 個觀光（打卡）點，若在任一觀光點打卡
該App就會預測遊客可能有興趣的其他觀光點

為了能夠準確預測觀光點，打卡公司設計了觀光景點相關性地圖
圖上有 $N$ 個點，分別以 $V_1, V_2, V_3, …, V_N$ 代表觀光點
並精心挑選了 $N−1$ 組觀光點以線段相連並依據經驗給定 $R_{i,j}$ 值，代表 $V_i$ 與 $V_j$ 的相關性
特別的是，該圖之任意兩點 $V_m$ 與 $V_n$ 一定有單一路徑 $p$ ，相互串連
而 $V_m$ 與 $V_n$ 的相關性就為該路徑上所有已知相關性的最小值 (即路徑上最小 $R_{i,j}$ 值)
如下圖 $V_1$ 到 $V_5$ 的 $R_{i,j}$ 值就是 $\min(5,3,1) \rightarrow 1$
請寫一個程式計算與任一觀光點 $V_k$ 相關性至少為 $q$ 的景點數量
輸入說明 : 第一行是 $N,V_k,q$，之後 $N-1$ 行是景點 $V_a V_b,R_{a,b}$

範例輸入 :
3 2 4
1 2 3
1 3 2

範例輸出 :
0

解析 :
這題是可以用 BFS 或是 DFS 從點 $V_k$ 去遍歷所有的點，只要在遍歷的同時加上路徑上的邊權重
要注意的大概有兩點
1. 有單一路徑的意思是**整張圖沒有環**，只需要用 BFS 或 DFS 去解
2. 在最開始的時候要注意 $R_{i,j}$ 設為 $q$ 以上

剩下的就跟先前的題目差不多，就是多了點變化

#include<bits/stdc++.h>
using namespace std ;
typedef pair<int, int> Pii ;
#define FF first
#define SS second

int main() {
    ios::sync_with_stdio(0), cin.tie(0) ;

    int n, vk, q ; // n 個節點 vk 起點 至少 q 相關性
    cin >> n >> vk >> q ;

    vector<vector<Pii>> G(n+1) ;
    for (int i=0;i<n-1;i++) {
        int a, b, w ;
        cin >> a >> b >> w ;
        G[a].push_back({b, w}) ;
        G[b].push_back({a, w}) ;
    }

    int ans = 0 ; // 答案
    vector<bool> R(n+1, false) ; // 每個節點的相關性
    queue<Pii> que ;
    R[vk] = true ;
    que.push({vk, q}) ;

    while (!que.empty()) {
        Pii now = que.front() ;
        que.pop() ;

        for (Pii &it: G[now.FF]) {
            if (!R[it.FF]) {
                // 新節點 nx, nw 為 nx 與 vk 的相關性
                int nx = it.FF, nw = min(now.SS, it.SS) ;
                que.push({nx, nw}) ;
                R[nx] = true ;
                if (nw >= q) ans++ ; // 相關性 >= q
            }
        }
    }
    cout << ans << '\n' ;
    return 0 ;
}

### 例題-ZJ i793. pC. WAKUWAKU 尋找興奮源 (⌓‿⌓)
[題目連結](https://zerojudge.tw/ShowProblem?problemid=i793)
安妮亞是一位小學一年級學生(但實際上她只有 $4$ 歲)
她每天最喜歡做的事，就是尋找能讓她興奮(WAKUWAKU)的來源
伊甸學園坐落於一個 $R$ 列、$C$ 行的矩形
左上角座標 ($0$, $0$)，右下角座標 ($R-1$, $C-1$)
對於每格的狀態，我們可以用數字來表示：
$0$ 表示該處可以通行
$1$ 表示該處有障礙物
$2$ 表示該處有能夠讓安妮亞興奮(WAKUWAKU)的東西
已知安妮亞一開始在第 $a$ 列、第 $b$ 行，也就是位置 ($a$, $b$)
每步只能向周圍(上、下、左、右)四個方向走一格
其中能夠讓安妮亞興奮(WAKUWAKU)的東西可能不只一個
並可以假設伊甸學園外圍四邊皆以障礙物包覆，且初始位置 ($a$, $b$) 必定不會是障礙物
(這題應該可以抓到 BFS 中很多人不知道的一個小細節，在 debug 的時候可以紀錄起來)

解析 :
跟一般的 BFS 一樣，題目給了起點跟要求的點，因為題目同時要求找**離起點最近的要求點**
要注意一個細節，題目說起點不會是障礙物($1$)，但是沒有說不會是 $2$，BFS也不會判斷到起點
所以在判斷 $2$ 的點時，要**把起點列入考慮**當中，這也是我上面講到的細節

#include<bits/stdc++.h>
using namespace std ;
typedef pair<int, int> Pii ;
#define FF first
#define SS second

int main() {
    ios::sync_with_stdio(0), cin.tie(0) ;

    int R, C, a, b ;
    int mm[4][2] = {0,1, 0,-1, 1,0, -1,0} ;
    cin >> R >> C >> a >> b ;

    vector<int> tmp(C) ;
    vector<vector<int>> G(R, tmp) ;

    for (int i=0;i<R;i++)
        for (int j=0;j<C;j++)
            cin >> G[i][j] ;
    
    if (G[a][b] == 2) { // 起點就是終點
        cout << "0\n" ;
        return 0 ;
    }
    queue<Pii> que ;
    que.push({a, b}) ;
    G[a][b] = -1 ;     //  用 -x 表示該點走了 x-1 步
    while (!que.empty()) { // BFS
        Pii now = que.front() ;
        que.pop() ;

        for (int i=0;i<4;i++) {
            int nx = now.FF+mm[i][0], ny = now.SS+mm[i][1] ;
            if (nx<R && nx>=0 && ny<C && ny>=0) {
                if (G[nx][ny] == 0) {
                    G[nx][ny] = G[now.FF][now.SS]-1 ; // 多走一步
                    que.push({nx, ny}) ;
                }
                else if (G[nx][ny] == 2) {
                    cout << -G[now.FF][now.SS] << '\n' ;
                    return 0 ;
                }
            }
        }
    }
    cout << "WAKUWAKU\n" ;
    return 0 ;
}

### 例題-ZJ k573. pD. 關於病毒傳播這件事
[題目連結](https://zerojudge.tw/ShowProblem?problemid=k573)
有一種奇怪的病毒在世界蔓延，科學家觀察以後發現該病毒具有以下特徵 ：
1. 病毒具有衰變性，從帶原者由內而外，最多只會往外傳播 $K$ 層，就不會再傳播給下個人
2. 病毒發生變異時，只會發生在傳播開始前(過程中無變異)，編號越大代表越新變異的病毒
3. 曾感染過的患者會帶有抗體，除非遇到更新型的變異株，否則該抗體可以抵禦較舊版本的病毒
4. 不會有已於先前發生事件得到新型抗體，但仍成為後來發生事件舊病毒最初帶原者的狀況
5. 在上次帶原事件傳播結束後下次事件才會發生，也就是不會有兩事件同時在傳播

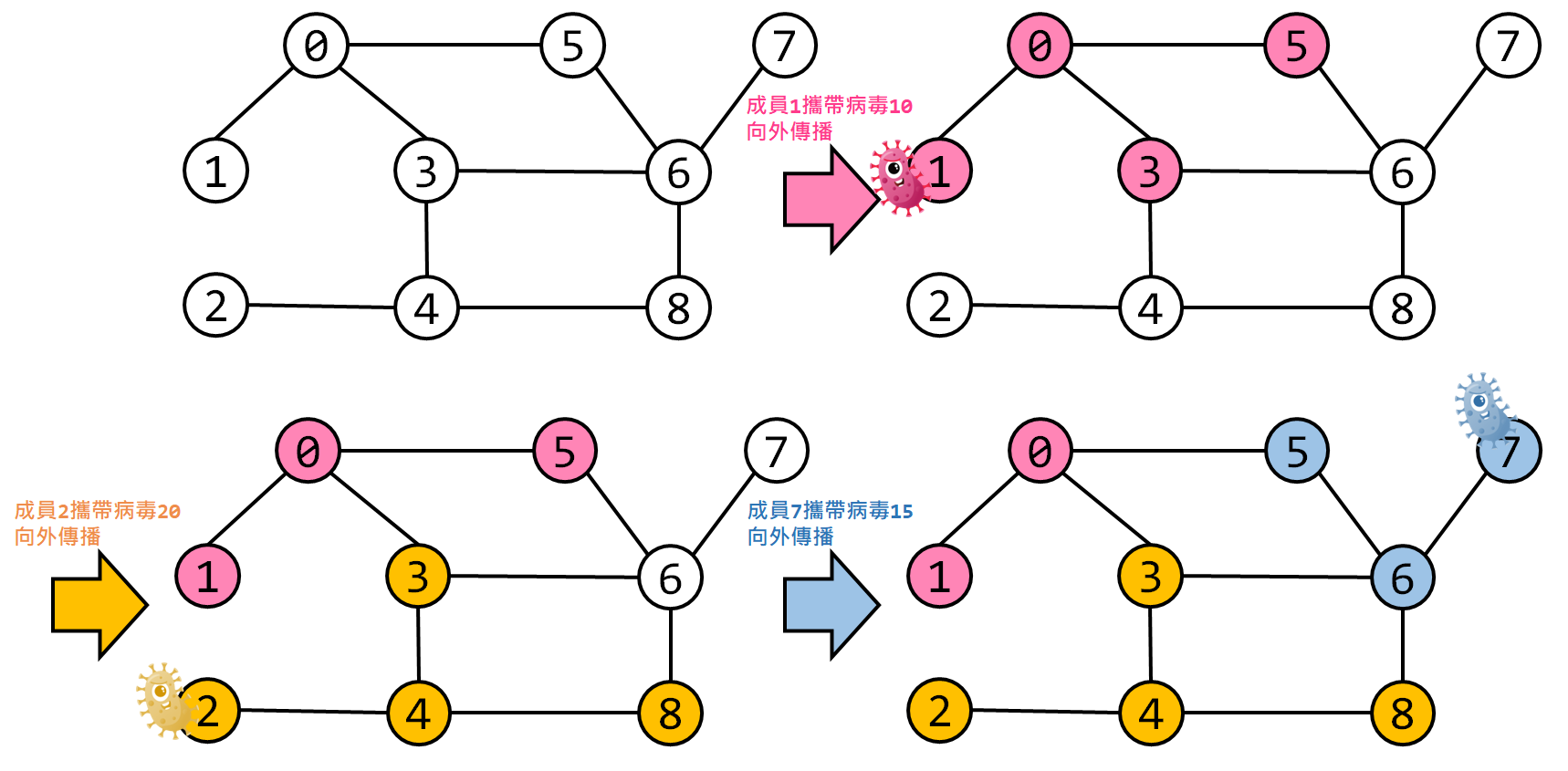
請計算該次事件傳播結束時，會受到該編號病毒感染的總人數(包含該次事件最初帶原者本身)

解析 :
從第一點來看，最多蔓延(遍歷) $K$ 層，其實就是與帶原者節點距離 $K$
所以用 BFS 會比較直覺，而第二點與第三點來看，如果某個點已經被傳染
但是抗體編號 < 病毒編號代表那個點還是可以被感染，所以我們假設原本所有節點抗體編號為 $0$
這樣無論起始病毒編號多小，都可以感染，而第四點代表每次新病毒只會在沒被感染過的人身上
而編號大小比較的問題就是在判斷點是否走過時**多加入一個條件**即可
而從第五點來看就是**多次 BFS**而已，實際上沒有難度，就是題目看起來複雜

#include<bits/stdc++.h>
using namespace std ;
typedef pair<int, int> Pii ;
#define FF first
#define SS second

int main() {
    ios::sync_with_stdio(0), cin.tie(0) ;

    int n, m, k, q ;
    cin >> n >> m >> k >> q ;

    vector<vector<int>> G(n) ;
    for (int i=0;i<m;i++) {
        int a, b ;
        cin >> a >> b ;
        G[a].push_back(b) ;
        G[b].push_back(a) ;
    }

    vector<int> gone(n, 0) ; // 各節點抗體編號

    for (int i=0;i<q;i++) {
        int a, b ;
        cin >> a >> b ;

        int ans = 1 ; // 共感染幾個編號(帶原者也算)
        queue<Pii> que ; // BFS
        que.push({a, 0}) ;
        gone[a] = b ;       
        while (!que.empty()) {
            Pii now = que.front() ;
            que.pop() ;
            if (now.SS == k) continue ;
            for (int &it: G[now.FF]) {
                if (b > gone[it]) {     // 病毒 > 抗體
                    gone[it] = b ;
                    que.push({it, now.SS+1}) ;
                    ans++ ;
                }
            }
        }
        cout << ans << '\n' ;
    }

    return 0 ;
}

### 例題-ZJ m933. 3. 邏輯電路(拓樸排序概念)
[題目連結](https://zerojudge.tw/ShowProblem?problemid=m933)

題目解析 :
首先要把整個電路的流程先搞清楚才能知道怎麼運算，搭配圖會比較好理解

1. 輸入段根據題目給定值進行輸入
2. 邏輯閘接收到對應數量的輸入後(例如 NOT 閘需要一個、其餘都是兩個)，就可以運算
3. 邏輯閘運算完後可以將輸出值傳到後方直接連接的 $n$ 個邏輯閘(例 $g7$ 傳到 $g9$)
4. 重複步驟 $2、3$，當所有邏輯閘都進行輸出完畢代表所有輸出端都有值

這四個步驟只要轉換成程式碼就可以了，依照步驟一個個講解
我們可以把整個電路看成一張圖，輸入、輸出端口和邏輯閘都是節點，電線就是相連節點的邊
然後做 BFS 從輸入端口開始，只要邏輯閘(節點)的輸入足夠了，就把邏輯閘放入 queue
然後再計算後繼續將其輸出輸入到下一個節點，重複如此就可以將輸出計算出來了
整理幾個題目的要求補充跟細節給各位
1. 防止輸出端做運算的方法有很多種: 用 index 判斷、設定除 NOT 閘不滿兩個輸入就不運算等
2. 計算延遲時間，因為 BFS 特性，越晚處理的節點延遲時間越大

以下程式碼因節省空間所以不同資料結構的 index 會比較複雜，腦子裡需要自已轉換
建議方便實作直接把所有資料結構的大小開到 (輸入端口數量+邏輯閘數量+輸出端口數量$+1$)

#include<bits/stdc++.h>
using namespace std ;
typedef pair<int, int> Pii ;
#define FF first
#define SS second

int main() {
    ios::sync_with_stdio(0), cin.tie(0) ;

    int p, q, r, m ;
    cin >> p >> q >> r >> m ;

    vector<int> in(p+1), gate(q+1) ; // 輸入端口、邏輯閘類型
    for (int i=1;i<=p;i++)
        cin >> in[i] ;
    for (int i=1;i<=q;i++)
        cin >> gate[i] ;

    vector<Pii> gin(q+r+1, {-1, -1}) ; // 邏輯閘輸入
    vector<vector<int>> G(p+q+1) ; // 邏輯閘連接
    for (int i=0;i<m;i++) {
        int a, b ;
        cin >> a >> b ;

        G[a].push_back(b) ;
    }

    int ans ; // 最大延遲時間 -> 因 BFS 特性可直接得知
    queue<Pii> que ; // BFS
    for (int i=1;i<=p;i++) // 將一開始輸入放入 queue
        que.push({i, 0}) ;
    while (!que.empty()) { 
        Pii now = que.front() ;
        que.pop() ;

        int out ; // now 閘 or輸出端口 的 輸出
        if (now.FF <= p) // 直接輸出
            out = in[now.FF] ;
        else {            // 根據閘計算輸出
            int idx = now.FF - p ;
            if (gate[idx] == 1) // AND
                out = (gin[idx].FF && gin[idx].SS) ? 1 : 0 ;
            else if (gate[idx] == 2) // OR
                out = (gin[idx].FF || gin[idx].SS) ? 1 : 0 ;
            else if (gate[idx] == 3) // XOR
                out = (gin[idx].FF != gin[idx].SS) ? 1 : 0 ;
            else if (gate[idx] == 4) // NOT
                out = (gin[idx].FF) ? 0 : 1 ;
        }
        ans = now.SS ; // 更新延遲時間
        for (int &it: G[now.FF]) {
            int idx = it-p ;
            if (idx <= q && gate[idx] == 4) { // not 閘只需一個輸入
                gin[idx].FF = out ;
                que.push({it, now.SS+1}) ;
            }
            else {                          // 其他閘都需要兩個輸入
                if (gin[idx].FF != -1) { 
                    gin[idx].SS = out ;
                    que.push({it, now.SS+1}) ;
                }
                else
                    gin[idx].FF = out ;

            }
        }
    }

    cout << ans << '\n' ;
    for (int i=q+1;i<q+r+1;i++)
        cout << gin[i].FF << ' ' ;
    return 0 ;
}

## 圖的單向特質與、DFS、BFS
在某些題目設定的情況下，圖只需要往某個方向傳遞資料，或是做運算等等
所以這時候在輸入圖時就可以直接將圖的邊紀錄成單向邊
舉幾個例子，比如有些樹的題目只需要從根往下走，或是可以藉由遞迴的方式傳遞資料(DFS)
那就不需要建立從子節點到父節點的邊，一般的電路也是這樣的，資料順序都是輸入-邏輯閘-輸出

### 例題-ZJ g309. pC. 傳遞杯子蛋糕(Cupcake)
[題目連結](https://zerojudge.tw/ShowProblem?problemid=g309)
題目解析 :
每個節點都有兩個(以下)個子節點，那就是二元樹，不過這個不是很重要
由於每個結點 $V$ 都要將自己的杯子蛋糕均分給子節點 $N$，而 $N$ 又需要將蛋糕均分給 $N$ 的子節點
這樣只需要從根節點向下考慮的情況，只需要單向邊就可以了
然後就是做 BFS + 均分的運算

#include<bits/stdc++.h>
using namespace std ;

int main() {
    ios::sync_with_stdio(0), cin.tie(0) ;

    int n, k ;
    cin >> n >> k ;

    vector<vector<int>> G(n) ;
    for (int i=0;i<n;i++) {
        int v, a, b ;
        cin >> v >> a >> b ;

        // 只需向下傳遞
        if (a != -1)
            G[v].push_back(a) ;
        if (b != -1)
            G[v].push_back(b) ;
    }

    vector<int> ans(n, 0) ;
    queue<int> que ;
    que.push(0) ;
    ans[0] = k ;
    while (!que.empty()) {
        int now = que.front() ;
        que.pop() ;

        int nk = ans[now] / (1+G[now].size()) ; // 子節點分到的蛋糕
        ans[now] -= nk * G[now].size() ; // 將父節點蛋糕分給子節點
        for (int &it: G[now]) { // 只會向下傳遞 -> 不可能回頭
            ans[it] = nk ;
            que.push(it) ;
        }
    }

    for (int &it: ans)
        cout << it << ' ' ;

    return 0 ;
}