## 定義
在數學或其他理科方面,或多或少都會用到一些數學概念,現在要將這些概念運用在程式上面
這裡的邏輯,大致上是在說明一些有關於電腦的運行與優化結構所需的知識,還有數學上的邏輯等
為了讓之後的教學不會遇到太多的阻礙,會先在這裡教一些概念應用到程式的例子或是純講概念
基本上這些內容大多都是國高中的基礎,或是之後上大學會用到的概念,
## 質數、因數和質因數分解
在數學上,只要 $a$ 可以被 $b$ 整除,我們就會說 $b$ 是 $a$ 的因數,$a, b$ 須為自然數
所謂的質數,就是其因數只有自身與 $1$ 的數字,比如 $7$ 的因數只有 $1,7$ 所以 $7$ 是質數
換句話說,只要找到某數 $X$ 有不是 $1、X$ 的因數,那 $X$ 就是質數,在程式中會像這樣
```cpp=
bool isprime(int x) { // true 代表 x 為質數
for (int i=2;i<x;i++)
if (x % i == 0) // i 為 x 的因數
return false ;
return true
}
```
某數 $X$ 的質因數代表其滿足質數的條件且同時是 $X$ 的因數,可以用以下方法輸出全部的質因數
```cpp=
void prime_factor(int x) {
for (int i=2;i<x;i++)
if (x % i == 0 && isprime(i))
cout << i << ' ' ;
return ;
}
```
如果需要質因數分解,就需要從質因數分解的結果反推分解過程需要甚麼,以下是分析
1. 質因數分解後會分成多項,每一項都只可能是質數,所以在分解前,只需要紀錄所有質因數
2. 承1. 每一項可能會有 $n$ 次($n > 1$),所以在分解時,質因數的次方數需要被計算並記錄
根據這兩點,我們的演算法大致上已經完成了,首先紀錄質因數,接著判斷次方數,最後完成分解
```cpp=
#include<bits/stdc++.h>
using namespace std ;
bool isprime(int x) { // true 代表 x 為質數
for (int i=2;i<x;i++)
if (x % i == 0) // i 為 x 的因數
return false ;
return true ;
}
int main() {
ios::sync_with_stdio(0), cin.tie(0) ;
int n ;
cin >> n ;
vector<int> prime_factor ; // 質因數列表
for (int i=2;i<n;i++)
if (n % i == 0 && isprime(i))
prime_factor.push_back(i) ;
int len = prime_factor.size() ;
int cnt ; // 次方數
for (int i=0;i<len;i++) { // 找到每個質因數的次方數
cnt = 0 ;
while (n % prime_factor[i] == 0) { // 計算次方數
cnt++ ;
n /= prime_factor[i] ;
}
// 輸出
cout << prime_factor[i] << '^' << cnt ;
if (i != len-1)
cout << " * " ;
}
return 0 ;
}
```
## 最大公因數(GCD)
如果 $a$ 是可以同時"被" $b,c$ 整除的最大可能,則 $a$ 是 $b,c$ 的最大公因數,$a,b,c$ 為自然數
反之如果 $a$ 是可以同時整除 $b,c$ 的最小可能,那 $a$ 就是 $b,c$ 的最小公倍數,$a,b,c$ 為自然數
不過我們這裡要處理的是多個數字的最小公倍數與最大公因數,先從最大公因數開始
這裡要用到輾轉相除法,對於某些人來說可能會比較陌生,相關的概念可以去看[這裡
](https://zh.wikipedia.org/zh-tw/%E8%BC%BE%E8%BD%89%E7%9B%B8%E9%99%A4%E6%B3%95)
我就直接實作了,不再重複去講述它的原理(~~主要是因為講起來有點麻煩~~)
```cpp=
int gcd(int a, int b) {
if (a % b == 0) return b ;
return gcd(b, a % b) ;
}
```
所有數的最大公因數就是重複找目前最大公因數與新數字的最大公因數,全部數字都找完後就是答案
```cpp=
#include<bits/stdc++.h>
using namespace std ;
int gcd(int a, int b) {
if (a % b == 0) return b ;
return gcd(b, a%b) ;
}
int main() {
ios::sync_with_stdio(0), cin.tie(0) ;
int n, ans, now ;
cin >> n ;
cin >> now ;
ans = now ; // 一個數的最大因數就是自己
for (int i=1;i<n;i++) {
cin >> now ;
ans = gcd(ans, now) ; // 一個個去做 gcd
}
cout << ans << '\n' ;
return 0 ;
}
```
## 矩陣乘法
在之後的內容可能會遇到矩陣相關的演算法,所以要提前復習一下矩陣乘法的算法
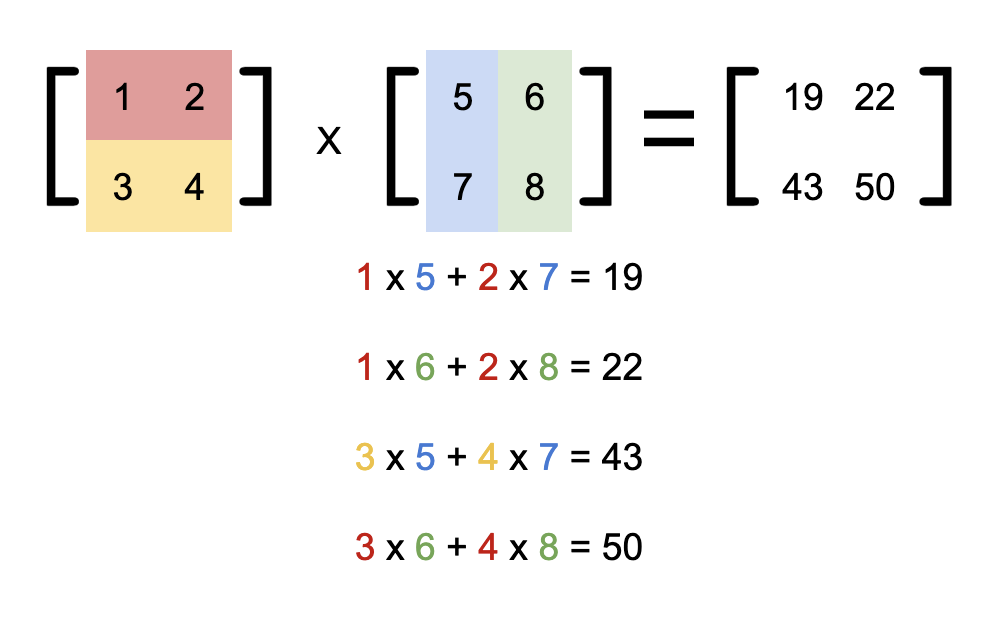
## 進制轉換
在電腦中都是使用 $2$ 進制儲存資料,不過我們生活中都是用 $10$ 進制去理解數字
比較特別的也有用類 $60$ 進制的秒 to 分鐘,或類 $24$ 進制的小時 to 天數等等
在這些不同進制的概念中,都可以用 $(x)_{a}$ 去表示 $a$ 進制的 $x$
---
關於任何小數前 $n+1$ 位小數後 $m$ 位的數字在 $a$ 進制都有一個通用的表達方式
* $x_n\times a^n + x_{n-1} \times a^{n-1} + ... + x_0\times a^0 + y_1\times a^{-1} + ... + y_m\times a^{-m}$
如果把 $(1234.5678)_{10}$ 用這種方式表達就是
$1*10^3+2*10^2+3*10^1+4*10^0+5*10^{-1}+6*10^{-2}+7*10^{-3}+8*10^{-4}$
那如何快速的計算不同進制轉換就變成最大的問題,最常見的就是用十進制轉二進制
這時候就會用到短除法,因為短除法的特性在這種轉換進制的地方很好用

至於二進制轉換成十進制就用上面的表達方式去做就好,以下程式碼去實現兩個功能
```cpp=
#include<bits/stdc++.h>
using namespace std ;
void dec_to_any(int a, int b) { // number a base 10 to base b
string s = "" ;
while (a) {
s += (char)('0'+(a % b)) ;
a /= b ;
}
reverse(s.begin(), s.end()) ;
cout << s << '\n' ;
return ;
}
void any_to_dec(string s, int b) { // number a base b to base 10
int times = 1, n = 0, len = s.size() ;
for (int i=len-1;i>=0;i--) {
n += (s[i]-'0') * times ;
times *= b ;
}
cout << n << '\n' ;
return ;
}
int main() {
dec_to_any(10, 2) ;
any_to_dec("1010", 2) ;
return 0 ;
}
```
---
不過為了增加硬體的效率,實際上可能不只會用二進制,八進制、十六進制也常常用在硬體當中
對於 $a$ 進制轉換成 $a_i$ 進制或是轉換回來的操作,也有很簡易的演算法
我們拿 $2$ 進制與 $16$ 進制來回轉換做例子,也就是 $2$ 進制與 $2^4$ 進制
假設要操作 $(10100011)_2$,我們把四個四個當作一組 $0011$ 變成 $3$,$1010$ 變成 A,最後就是 $A3$
那轉換回來也視同個概念,一個可以轉換成四個一組,$A$ 轉換成 $1010$,$3$ 轉換成 $0011$
所以概念上 $a$ 進制轉換成 $a_i$ 進制就是要把 $i$ 個做成一組
---
在某些情況下如果出現循環小數,就會在電腦的二進制無法完美儲存,所以會有浮點數精度的問題
對於這種問題,可以透過分開儲存小數部分或是先進位到整數等等方式,在別的篇章會說明
## 集合 (set)
集合是由不同元素組成的,集合中的元素不會出現重複
如果集合中沒有任何元素,則稱為"空集合"
假設有兩個集合 $A, B$,若所有 $B$ 中的元素都出現在 $A$ 中,則稱 $B$ 為 $A$ 的子集(子集合)
包含所有定義範圍中元素的集合叫做全集(Universe set),常用 $U$ 表示
在程式會使用到的集合中,會有以下比較常見的操作 :
1. 加入元素
2. 刪除元素
3. 判斷是否為空集合
4. 判斷某個元素是否在集合中
5. 判斷某個集合是不是另外一個集合的子集
6. 聯集(union): 包含所有在 $A$ 或 $B$ 的元素
7. 交集(Intersection): 包含所有"同時"在 $A$ 和 $B$ 的元素
8. 差集(Difference): 包含所有在 $A$ "但"不在 $B$ 的元素
9. 補集(Complement): $U$ 和 $A$ 的差集就是 $A$ 的補集
一般在程式當中,用 STL 的 set 就可以解決大部分的問題
## 取餘
所謂的取餘在各種演算法、競賽題目當中很常看到,這裡簡單介紹一下
定義: $a\ mod\ m = r$ 代表 $a=qm+r$,其中 $q$ 是整數且 $0\le r<m$
基本上在程式競賽中是為了不要讓數字太大導致溢位或是為了有循環數字(循環 index 等)
下面介紹一些基礎計算搭配上取餘
1. $(a+b)\ mod\ m = ((a\ mod\ m)+(b\ mod\ m))\ mod\ m$
2. $(a-b)\ mod\ m = ((a\ mod\ m)-(b\ mod\ m))\ mod\ m$
3. $(a\times b)\ mod\ m = ((a\ mod\ m)\times (b\ mod\ m))\ mod\ m$
4. $(a^b)\ mod\ m = ((a\ mod\ m)^b)\ mod\ m$
以上四個計算都可以拓展至更長的計算當中,並且注意沒有除法
比如 $(a+b+c+...)\ mod\ m = ((a\ mod\ m)+(b\ mod\ m)+(c\ mod\ m)+...)\ mod\ m$
還有另外一個要注意的地方是 C++ 的`%`可能會產生負數
```cpp=
-3 % 5 == -3
// 解決方式
((a % m) + m) % m // 確保數字在 0 ~ (m-1) 之間
```
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet