## 樹
樹的定義是：任**兩點之間都相通**，並且沒有「環」的圖，「環」在前面有介紹，是**起終點相同**的路徑
如果下圖點 $5$ 和點 $6$ 相連，就不能稱作樹，因為有一條 $\{5,2,1,3,6,5\}$，起終點相同的路徑
有根樹會像是這樣 :

轉換成無根樹就表示成這樣

## 樹的名詞
有根樹、無根樹 : 是否有指定根節點(指定根)
通用(有根樹與無根樹)名詞 :
1. 森林 (forest) : 每個連通塊都是樹的圖
2. 生成樹 (spanning tree) : 一個連通無向圖的子圖，在圖的邊集合裡選 $n − 1$ 條邊將所有頂點連通，會滿足一棵樹
3. 葉節點 (leaf node) : 無根樹上度數不超過 $1$ 的點 / 有根樹上沒有子結點的點

有根樹專用 :
1. 父節點 (parent node) : 一個結點到根結點路徑上的第二個點，根結點沒有父親
2. 祖先 (ancestor) : 一個結點到根結點路徑上除了自身以外的所有結點
3. 子結點 (child node) : 若 $u$ 是 $v$ 的父親，則 $v$ 是 $u$ 的子節點
5. 深度 (depth) : 根節點到某個點路徑上經過的點的數量
6. 高度 (height) : 所有節點深度的最大值
7. 子樹 (subtree) : 由某個點以及其子孫所組成的樹

雖然這些名詞只在有根樹才能使用，但在某些問題當中，無根樹也需要指定某個節點為根
或是採用虛擬根的方式，這時候使用這些名詞也行

簡單介紹一下有根樹，可以把現實中的樹倒轉放上去，最上面的點 $1$ 叫做根，最下面的則叫葉
樹可以分層，根據不同的方式會有不同結果(例如:從上到下、從上到下、改變根)
例如這張圖從上到下分層就會如上圖所示，基本上現階段不太會因為方式影響
如果點之間有上下關係(例如: $1,2,5$ )，則將 $1,2$ 稱為 $5$ 的祖先，最靠近 $5$ 的點 $2$ 稱為 $5$ 的父節點
相反的，如果點 $A$ 是點 $B$ 的祖先，點 $B$ 是點 $A$ 的子孫，父節點對應的就是子節點
所以從定義可以知道，根結點**沒有祖先**，也**沒有父節點**，解題時可以用這個做為判斷根的方法
目前介紹這些就夠了，之後的名詞會出現在題目或觀念之中，而無根樹先不介紹也行
最重要的是，樹只是有著些許特性的圖，所以圖的遍歷( DFS、BFS )**可以**應用在樹上
但是樹的**特殊點之間路徑**可以不用到 DFS 或是 BFS，這個方式在例題當中會說明

## 樹的特性
1. 樹不可能有環 => 是樹或是森林
2. 樹上所有點之間都相連通
3. 任意兩點之間只有唯一一條路徑
4. 在樹上任意兩點間添加一條邊，就會產生環
5. 在樹上任意刪除一條邊，一顆樹就會變成兩棵樹
6. 邊數等於點數 $-1$ => 無重邊、連通、$n-1$ 邊就是樹
7. 除了根之外，其餘點都有且只有一個父節點 => 無父節點的為根
8. 除了葉節點之外，其餘節點都有一個以上的子節點 => 無子節點為葉節點

第一點+第二點就可以判斷是樹還是森林(多棵樹)，因為多棵樹是**獨立分開**的多個圖
但是如果把**多棵樹都放到同一張圖**，就會變成像是一塊塊的區域，區域當中沒有連通
所以第一點滿足後，只要考慮第二點就可以判斷樹或是森林，第三點應該可以**直接從圖上判斷**
而第四點的概念是，添加一條邊就會產生環，因為第二點有說樹上任意點之間連通
也就是說任意點之間有路徑，此時如果再多加一條邊，就會讓該路徑能夠回到原出發點
第五點可以把範圍縮小看，樹的邊連接的兩點一定為父子節點，此時斷掉邊，就會產生一棵子樹
子樹外(有原父節點)的地方就算少了這棵子樹也還是樹，所以一棵樹會變成兩棵樹
第六點

## 樹的存法
樹也是圖的一種，所以圖的各種存法(Adjacency Matrix、Adjacency List等)皆可
不過在上述的介紹當中，已經有說明子節點跟父節點的關係，可以根據這個關係來存樹
也可以用原本存圖的方式存樹，所以這邊會介紹如何根據題目特性調整圖的細節
利用 Adjacency Matrix、Adjacency List 的方法依然在大多數情況下通用
這邊就不特別介紹了，因為就是很基本的存圖方法，之前介紹過了

剛剛說到可以用父子節點關係來存圖，以下就是一個例子，但不是每一題都建議這樣做
只有在確定題目只需要某一方向或是需要明確各點的父子關係時才比較易於使用
樹需要從葉節點開始往上走(紀錄每個點的父節點)，反之從根結點往下走(紀錄每個點的子節點)

#include<bits/stdc++.h>
using namespace std ;

int main() {
    ios::sync_with_stdio(0), cin.tie(0) ;

    int n, m, u, v ; // n nodes, m edges, node u, node v
    cin >> n >> m ;
    vector<int> G[n] ; // graph
    for (int i=0;i<m;i++) { // undirected
        cin >> u >> v ;
        G[u].push_back(v) ;
        G[v].push_back(u) ;
    }

    // assume 0 is root
    vector<bool> gone(n, false) ;
    vector<int> child[n] ;
    vector<int> parent(n) ;
    queue<int> que ;
    que.push(0) ;
    gone[0] = true ;
    parent[0] = -1 ;

    while (!que.empty()) {
        int now = que.front() ;
        que.pop() ;

        cout << now << '\n' ;
        for (int &it: G[now]) {
            if (!gone[it]) {
                gone[it] = true ;
                que.push(it) ;
                parent[it] = now ;
                child[now].push_back(it) ;
            }
        }
    }

    for (int i=0;i<n;i++)
        cout << "parent of " << i << " is " << parent[i] << '\n' ;
    for (int i=0;i<n;i++) {
        cout << "child of " << i << " : " ;
        for (int &it: child[i]) {
            cout << it << ' ' ;
        }
        cout << '\n' ;
    }
    return 0 ;
}

(註: 使用 DFS 也可以做到相同效果，可以自行查詢思考)

## 樹兩點間的距離
在無權重的情況下，兩點間的距離就是兩點之間的邊數，基本上從某點開始做 BFS/DFS 就可以了
## 子樹
定義為**把某點 $X$ 當作根**，然後"只"保存 $X$ 與 $X$ 的所有子孫節點，其餘節點去除
例如下面那張圖上把 $2$ 當作根，子樹就會是 $/{2,4,5/}$ 組成的樹，子樹就是**樹上切割下來的樹**
如下圖**紅色框中區域**，現在有兩個問題可以幫助各位快速了解子樹

1. 如上圖，給定一樹，問點 $2$ 的子樹大小(共有幾個點)
2. 問各點的子樹大小

請先將題目給的圖存入程式當中，在用程式解決上述兩個問題

問題一解析 :
用圖的思路去解題，樹只是變形的圖，所以如果要找點 $2$ 的子樹
就只是用單向圖把 $2$ 當作根做 DFS，把 $2$ 所有子節點 $X$ 的子樹大小相加後 $+1$ 就是答案

#include<bits/stdc++.h>
using namespace std ;

int dfs(int now, vector<vector<int>> &G) {
    int ans = 1 ; // 目前節點
    for (int &it: G[now]) { // 子節點的子樹大小
        ans += dfs(it, G) ;
    }
    return ans ; // 回傳目前節點子樹大小
}

int main() {
//    ios::sync_with_stdio(0), cin.tie(0) ;

    vector<vector<int>> G(7) ;
    G[1].push_back(2) ;
    G[1].push_back(3) ;
    G[2].push_back(4) ;
    G[2].push_back(5) ;
    G[3].push_back(6) ;

    int ans = dfs(2, G) ;
    cout << ans << '\n' ;

    return 0 ;
}

在這種情況下只要把各點當作根就可以知道所有點的子樹大小
但如果需要一次詢問多個節點的子樹大小，就用一個陣列儲存節點子樹大小，然後從根做 DFS
因為**樹根開始才能涵蓋到整棵樹**，這裡也有概念相似的題目，可以直接用 DFS + 陣列
## 例題-ZJ d459. 一棵小樹
[題目連結](https://zerojudge.tw/ShowProblem?problemid=d459)

解題思路 :
注意這題需要判斷父節點與子節點的關係，所以要用無向邊，需要額外用 bool 陣列表示是否走過
不過因為用 DFS 肯定會先走過父節點，所以父節點可以先將子樹大小設為 $1$，表示父節點本身
這樣就可以省去陣列，在子節點時判斷子樹大小是否為 $0$ 來去除回頭走父節點的可能

#include<bits/stdc++.h>
using namespace std ;

int ans[20005] = {0} ;

void dfs(int now, vector<vector<int>> &G) {
    ans[now] = 1 ;
    for (int &it: G[now]) {
        if (ans[it] == 0) { // 去除父節點
            dfs(it, G) ;
            ans[now] += ans[it] ;
        }
    }
    return ;
}

int main() {
    ios::sync_with_stdio(0), cin.tie(0) ;

    int n ;
    cin >> n ;

    vector<vector<int>> G(n+1) ;
    for (int i=1;i<n;i++) {
        int a, b ;
        cin >> a >> b ;

        G[a].push_back(b) ;
        G[b].push_back(a) ;
    }

    dfs(1, G) ; // 從根開始
    for (int i=1;i<=n;i++) // 輸出格式化的答案
        cout << setw(5) << i << "-" << setw(5) << ans[i] << '\n' ;

    return 0 ;
}

---
不過子樹大小還可以透過葉節點往上做 BFS，以下是實際做法

#include<bits/stdc++.h>
using namespace std ;

int main() {
//    ios::sync_with_stdio(0), cin.tie(0) ;

    vector<int> G(7) ;
    G[2] = 1 ;
    G[3] = 1 ;
    G[4] = 2 ;
    G[5] = 2 ;
    G[6] = 3 ;

    vector<int> ans(7, 0) ; // 子樹大小
    queue<int> leaf ; // 所有葉節點
    leaf.push(4) ;
    leaf.push(5) ;
    leaf.push(6) ;

    while (!leaf.empty()) {
        int now = leaf.front() ;
        leaf.pop() ;
        ans[now]++ ; // 本身作為子樹 root -> 節點數+1
        if (ans[G[now]] == 0) // 該節點尚未加入路徑or未走過
            leaf.push(G[now]) ;
        ans[G[now]] += ans[now] ; // 將子節點子樹數量加到父節點子樹
    }

    for (int i=1;i<7;i++)
        cout << "size of sub tree of node " << i << " is " << ans[i] << '\n' ;
    return 0 ;
}

## 樹的高度
之前有稍微提到樹的高度，詳細定義是點 $A$ 到其距離最遠的子孫(葉節點)的距離

如上圖，點的高度寫在點右上角，舉樹根點 $1$，它子孫中的葉節點只有 $/{2,5,6/}$
而點 $6$ 距離樹根最遠，所以點 $1$ 跟點 $6$ 的距離就是**樹根的高度**
單一點求高度的方式已經知道了，就是用 DFS 或是 BFS 找距離點最遠的子孫
如果要求出所有的點高度，那就必須先知道一些由定義推論出來的概念
1. 葉節點的高度都是 $0$
2. 父節點的高度就是找 `max(各子節點的高度)+1`

第 $2$ 點可以看節點 $3$，節點 $3$ 有節點 $4,5$ 兩個節點，而節點 $3$ 的高度就是 max($0+1, 1+1$) $\rightarrow$ $2$
所以在遍歷整棵樹的時候，父節點的高度需要依據子節點判斷，這個特性就只能用 DFS
因為 BFS 是上一層完全結束才進入下一層，所以在討論點的深度可以用 BFS
但點的高度則相反，所以用 DFS 遞迴的特性才能讓子節點**回傳數值**給父節點
(範例用有向邊做舉例，如果遇到無向邊，可以用一維陣列紀錄走過的路)

## 例題-ZJ f673. FJCU_109_Winter_Day2_Lab1 樹高(樹高度的求法)
[題目連結](https://zerojudge.tw/ShowProblem?problemid=f673)
按照題目測資來看，樹的高度是樹的根到與根距離最遠的葉之間的距離(路徑上有幾個邊)
只要從所有葉節點開始往上計算，就可以計算出每個節點的高度，而根節點的高度就是樹的高度
其實**樹的層數 $-1$ 就是它的高度**，所以在判斷樹高度的時候，可以從**根往下找所有的葉**
距離根**最遠的**葉就會是最終目的地，由於這題的樹只會有一個方向，也就是**由上往下**走
所以在存圖的時候可以用有向邊的方式去存，這樣做的好處有兩個
1. 保證圖在遍歷的時候**只會往下走**
2. 不需要考慮走過的點，因為不會有**回頭**的情況

優點就是能省下 bool 陣列的空間和可以直接避免回頭的問題
最後只要用 BFS/DFS 就可以找到樹的高度(層數 $-1$ )
因為 BFS 優先處理同一層的點，所以最後處理的層數有也只有與根節點距離最遠的葉節點
DFS 則是用遞迴的方式將最高的層數一步步計算並回傳

#include<bits/stdc++.h>
using namespace std ;

int dfs(int now, vector<vector<int>> &G, int lvl) { // DFS
    int ans = lvl ; // 最大深度
    for (int &it: G[now])
        ans = max(ans, dfs(it, G , lvl+1)) ;
    return ans ;
}

int main() {
    ios::sync_with_stdio(0), cin.tie(0) ;

    int n ;
    cin >> n ;

    vector<vector<int>> G(n) ;
    for (int i=0;i<n;i++) { // 只需單向
        int a, b, c ;
        cin >> a >> b >> c ;
        if (b != -1) 
            G[a].push_back(b) ;
        if (c != -1)
            G[a].push_back(c) ;
    }

    int ans = dfs(0, G, 0) ; // 從根(編號 0)開始
    cout << ans << '\n' ;

    return 0 ;
}

題目結束後再補充一下樹的深度，某點的深度就是**根到某點的距離**
也就是說樹的高度其實也是所有點中深度最大值，可以用 BFS 或是 DFS 去解
但是 DFS 要用一個值去比大小， BFS 只要紀錄最新(目前距根最遠)的點就可以了
而某點的高度則跟樹的高度找的方式相同，比如根節點的高度就是樹的高度
至於其他點的高度，可以嘗試把樹切割成一個個分區，也就是下一段介紹的子樹
當然如果要求出所有點的高度，還是用 DFS 去找會比較快

## 例題-ZJ c463. apcs 樹狀圖分析 (Tree Analyses)
[題目連結](https://zerojudge.tw/ShowProblem?problemid=c463)
給定樹的節點數量與各點的子節點，問樹的根與各點高度總和

題目解析 :
題目當中並沒有說到哪一個點是根，所以要藉由根的特性去判斷，之前介紹父子節點有說過
"根沒有父節點"可以當作判斷的依據，在給定各點的子節點時，就可以記錄每個點的父節點
不過這裡採用比較小巧思的方法，就是將所有點編號總和-出現過確定是子節點的節點編號
因為根節點沒有父節點，所以不可能是子節點，其餘點都會被減去，剩下自然就是根節點編號
最後在從根開始 DFS，就可以算出所有點的高度，唯一要注意的是題目給的 $N$ 最大到 $100000$
所以樹的高度總和最大會是樹成一直線時，數字大約為$\frac{100000\times(1+100000)}{2}$ 已經超過 int 範圍了
所以計算高度總和的變數改用 long long int 才能完全正確

#include<bits/stdc++.h>
using namespace std ;
typedef long long LL ;

LL ht = 0 ; // 記得改 long long

int dfs(int now, vector<vector<int>> &G) {
    int h = 0 ; // 目前樹高度
    for (int &it: G[now]) { // 有向邊
        h = max(h, dfs(it, G)+1) ;
    }
    ht += h ;
    return h ;
}

int main() {
    ios::sync_with_stdio(0), cin.tie(0) ;

    int n, rt ;
    cin >> n ;

    rt = ((n+1)*n) / 2 ; // 1~n 相加
    vector<vector<int>> G(n+1) ;
    for (int i=1;i<=n;i++) {
        int k, a ;
        cin >> k ;
        for (int j=0;j<k;j++) {
            cin >> a ;
            G[i].push_back(a) ; // 只需要有向邊
            rt -= a ; // 不是根就減去
        }
    }

    dfs(rt, G) ; // 從根開始 DFS 找個各點高度
    cout << rt << '\n' << ht << '\n' ;
    return 0 ;
}

## 樹的直徑
定義為樹上任兩點的最遠距離，按照定義，似乎要求所有點對點的距離才能找到答案
但是考慮到這兩點跟樹根的關係，就能用比較簡單的方式解決，首先要判斷樹根的位置

如上圖，樹的直徑可以是點 $6$ 到點 $4$ 或點 $5$，也就是說，如果要兩點距離最大
兩點必須要在根的**左右兩邊**，如果在同一邊，比如點 $4$ 跟點 $5$，之間的距離就會**比較小**
當然樹根不一定只有接兩條邊，如果有多個邊，那只要找不同邊延伸出去的點即可
用之前教過的**深度**來說，找不同邊的兩個最大深度相加就是直徑
但用 BFS 找不同邊的深度很困難，因為 BFS 是一層一層遍歷，所以不同邊很難紀錄
所以這邊可以用剛剛說的高度延伸去解決，DFS 一次解決一條邊的所有點
兩個不同邊的最遠距離點就可以很簡單地被記錄了

#include<bits/stdc++.h>
using namespace std ;

int point_high[7] = {0} ;

int dfs(int now, vector<int> G[]) {
    int h = 0 ;
    for (int it:G[now]) {
        h = max(h, dfs(it, G)+1) ; // 子節點高度+1
    }
    point_high[now] = h ; // 紀錄點的高度
    return h ; // 回傳節點高度給父節點
}

int main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0) ;

    vector<int> Tree[7] ;
    Tree[1].push_back(2) ; // 範例圖
    Tree[1].push_back(3) ;
    Tree[3].push_back(4) ;
    Tree[3].push_back(5) ;
    Tree[4].push_back(6) ;

    int h1 = 0, h2 = 0, tmp ; // 需保證 h1 >= h2
    for (int it:Tree[1]) {
        tmp = dfs(it, Tree)+1 ;
        if (tmp > h1) { // 找到目前最大高度
            h2 = h1 ;
            h1 = tmp ;
        }
        else if (tmp > h2) // 找到目前第二大高度
            h2 = tmp ;
    }

    cout << "樹的直徑: " << h1+h2 ;

    return 0 ;
}

## 無根樹的半徑
圖的"半徑"定義為選定任一個起點，能讓"起點到任意點的最長距離"最短
而無根樹的"半徑"定義為選定任一個點作為樹根，能使樹的高度最小

換句話說，就是要找出任一點作為樹根時"根到最遠的葉節點距離"最短
其實可以回想一下樹的直徑，有三個比較重要的點
1. 樹的直徑一定經過根節點
2. 樹的直徑由根的兩個"不同"子節點的子孫葉節點相連
3. 這兩個葉節點還滿足與根節點距離第一/二遠

根據第三點，假設這兩個葉節點與根的距離越相近，就能讓樹的高度越小
所以我們的問題就轉化成如何在無根樹中找到樹的直徑(樹上任兩點的最長距離)
這時候我們就可以用兩次 BFS/DFS 就可以找到樹直徑的兩個葉節點([證明過程](https://hackmd.io/@apcser/BJqRimtPxe))
找到樹直徑後，半徑就是 $\lceil \frac{X}{2} \rceil$，稍微推論就可知(兩葉節點與根距離相近)

#include<bits/stdc++.h>
using namespace std ;

int main() {
    ios::sync_with_stdio(0), cin.tie(0) ;

    int n ;
    cin >> n ;
    vector<int> G[n] ;
    for (int i=0;i<n;i++) {
        int m, x ;
        cin >> m ;
        for (int j=0;j<m;j++) {
            cin >> x ;
            G[i].push_back(x) ;
            G[x].push_back(i) ;
        }
    }

    vector<bool> gone(n, false) ;
    queue<int> que ;
    que.push(0) ;
    gone[0] = true ;

    int s, e ; // s: 與 0 距離最遠的點(也是直徑的兩端之一)
    while (!que.empty()) {
        int now = que.front() ;
        s = now ;
        que.pop() ;

        for (int &it: G[now]) {
            if (!gone[it]) {
                que.push(it) ;
                gone[it] = true ;
            }
        }
    }

    vector<int> road(n, -1) ; // s 到任意點距離
    que.push(s) ;
    road[s] = 0 ;
    while (!que.empty()) {
        int now = que.front() ;
        e = now ;
        que.pop() ;

        for (int &it: G[now]) {
            if (road[it] == -1) {
                que.push(it) ;
                road[it] = road[now] + 1 ;
            }
        }
    }

    cout << "Diameter of tree is " << road[e] << '\n' ;
    int rad = (road[e] % 2) ? road[e]/2+1 : road[e]/2 ;
    cout << "Radius of tree is " << rad << '\n' ;
    return 0 ;
}

還有另外一種利用逐漸刪除葉節點來定位中心點(也就是樹根)的方式找出半徑
不過難度太高，理解起來也會比較複雜，所以這裡就不花時間講述

## 樹的祖孫關係判斷
之前在樹的存法時有講過可以用 DFS、BFS 來找出父子關係
由於在樹當中，每個節點不斷往上找父節點就會找到根(根沒有父節點作為終點)

bool ancestor1(int a, int b, vector<int> &prt) {
    if (prt[a] == -1) return false ;
    if (prt[a] == b) return true ;
    return ancestor(prt[a], b, prt) ;
}

bool ancestor2(int a, int b, vector<int> &prt) {
	for (a=prt[a];a!=-1;a=prt[a])
		if (a == b)
			return true ;
	return false ;
}

以上程式碼就可以判斷出 $b$ 是否為 $a$ 的祖先(換句話說就是 $a$ 是否為 $b$ 的子孫)
在最壞的情況下時間複雜度可能會到 $O(H)$，此時 $H$ 是樹的高度

### LCA 最低共同祖先前瞻
在有根樹 $T$ 中，任意兩節點 $u$ 和 $v$，$LCA(u, v)$ 是"距離根最遠並且同時是兩節點的祖先"的節點
用比較通俗的話說，LCA 必須同時是兩節點的祖先，並且與兩個節點距離最短
不過比較特殊的是，如果 $u$ 是 $v$ 的祖先(或反過來)，那 LCA 會是 $u$，也就是節點本身
用最暴力的方法就是把兩點某一點的祖先記錄起來，然後找另一點的祖先時同步判斷共同祖先

int LCA(int a, int b, vector<int> &prt) {
    vector<int> acnt_a ; // ancestor of a
    while (a != -1) { // find ancestor of a
        acnt_a.push_back(a) ;
        a = prt[a] ;
    }

    while (b != -1) { // find ancestor of b
        for (int &it: acnt_a) { // find same ancestor
            if (it == b) return it ;
        }
        b = prt[b] ;
    }

    return -1 ;
}

演算法時間複雜度最壞為 $O(H)$，而且多次查詢就會效率很差
之後會有比較高效率的方式，但目前還不需要知道

## 樹壓平前瞻
[j124. 3. 石窟探險-題目連結](https://zerojudge.tw/ShowProblem?problemid=j124)
有一組探險隊要去一個樹狀結構的石窟內探險，該石窟內有 $N$ 個石室，每個石室都有編號
編號如果是偶數則會有兩個分支，如果是奇數則有三個分支
探險隊想要紀錄這個石窟的結構，每次只要第一次走到一個新的石室
就會將該石室的編號記錄在紙上，並由左到右依序走訪該石室的所有分支
若走到一條死路(無分支)則會在紙上紀錄一個數字 $0$
若已經走完所有分支則退回上一個石室，走訪完整個石窟後在紙上得到一個數字序列
探險隊回到基地後忘記計算了這個石窟內所有相鄰的石室編號相差取絕對值的總和
題目會給定紙上的數字序列，請幫助探險隊從推算出該數值
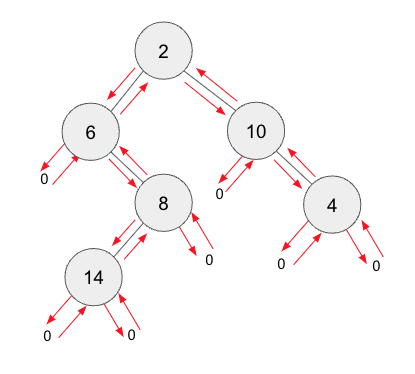
$|2 - 6| + |6 - 8| + |8 - 14| + |2 - 10| + |10 - 4| = 26$

範例輸入 :
2 6 0 8 14 0 0 0 10 0 4 0 0

範例輸出 :
26

分析 :
在題目敘述中可以知道，"在走訪完所有分支後回到前一個石室" 跟 DFS 完全相同
所以題目給的數字序列其實是石室的探索順序，也就是 DFS 的順序，在幫各位整理幾個重點
1. 偶數編號有兩個分支，奇數編號有三個分支
2. 從圖中可以知道相鄰的石室就是父節點跟子節點
3. 無分支的時候不能把 $0$ 當作子節點

所以最後用一個 DFS 逆推出答案即可

#include<bits/stdc++.h>
using namespace std ;

int now ;
long long ans = 0 ;
void dfs(int fat) { // fat 是父節點
    cin >> now ;    // 輸入子節點
    if (now == 0)
        return ;
    int num = now ; // 如果只用 now 父節點會被修改
    if (fat != 0) // 計算值(要避免計算到第一個值)
        ans += abs(num-fat) ;
    if (num % 2 == 1) // 奇數
        for (int i=0;i<3;i++)
            dfs(num) ;
    else             // 偶數
        for (int i=0;i<2;i++)
            dfs(num) ;
}


int main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0) ;
    dfs(0) ; 
    cout << ans ;
    return 0 ;
}

## 樹的遍歷/走訪
分為前序(preorder)、中序(inorder)、後序(postorder)和

## 二元樹-binary tree
樹中任一節點，最多只有兩個分支(最多兩個子節點)，最少無分支(無分支的即為葉節點)
因此不像 linkedlist 僅需要去存放下一個節點的記憶體位址即可
至少需要兩個指標變數去存放左邊的分支與右邊的分支
而這棵樹節點內部可以依照需求放置不同 type

---
而最基礎的二元樹結構就是

struct node {
    int val ;
    node* parent ;
    node* left ;
    node* right ;
};

這樣的好處就是節點可以是任意的數值，比如字元、非 $0$ 開始的數字甚至是字串等
而且如果用 vector 就可以將二元樹擴充到 $n$ 元樹，動態修改樹的操作也很簡單
但缺點就是需要管理記憶體動態分配的問題，並且也不能表達無根樹
動態記憶體分配在實際調用的情況下也會比 vector 慢一點

新增節點的方式也很簡單

node* new_node(int val, node* parent) { // make a new node
    node* nnode = new node ;
    nnode->val = val ;
    nnode->parent = parent ; 
    nnode->left = nnode->right = NULL ;
    return nnode ;
}

---
另一種方式是用二進制數字對應到節點，根就是 $1$，整體樹會像是這樣

                                       001
                                      /   \
                                    010   011
                                   /   \
                                 100   101 ...

如果有看出規律就可以發現，假設從上到下為第一層、第二層...
那第一層的節點就是 $2^0\sim2^1-1$，第二層就是 $2^1\sim2^2-1$，第三層就是 $2^2\sim2^3-1$
而父子節點的關係也有規律，就是父節點左移 $1$ bit (乘以 $2$) 後 $+0$ 和 $+1$
實際的做法在下方

int tree[1024] = {0} ; // root is 1
cout << "left, right node of root are " << 1*2 << ' ' << 1*2+1 ;

這種方式的優點就是速度很快、程式碼很簡潔，缺點是浪費多餘空間、會受樹高度限制
因為要符合規律，無節點的數值編號只能空著，而樹需要很高的話，就需要把每一層的空間都空出來
規律為以下兩點
1. 對於任意節點(編號為 $i$)，若有子節點，其左方子節點編號為 $2i$, 右方子節點編號為 $2i+1$
2. 對於任意節點(編號為 $i$)，若有父節點，其父節點編號為 $/frac{i}{2}$

## 二元樹的名詞解釋
1. full binary tree: 除了葉節點，其他節點都有兩個分支(兩個子節點)
2. complete binary tree: 最後一層未滿的節點皆靠左，其餘層數節點皆滿
3. perfect binary tree ：各層節點全滿，同時也是 $1$ 和 $2$

第一個為滿二元樹，共有 $2^h-1$ 個節點，$h$ 為樹高度，是同高度二元樹的節點上限

## 二元樹的遍歷
遍歷二元樹就是跑過整顆二元樹，總共有四種方式，但其實都是用 BFS/DFS 做變化
1. preorder traversal 前序遍歷: 根、左子樹、右子樹
2. inorder traversal 中序遍歷: 左子樹、根、右子樹
3. postorder traversal 後序遍歷: 左子樹、右子樹、根
4. level-order traversal 層序遍歷: 同一層排一起(不太重要，可忽略)

前三個都是用 DFS，但內容會根據順序變化，最後一個用 BFS 做，概念也很簡單
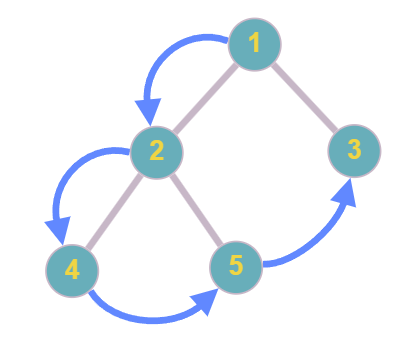
以上是一個前序的範例，先從根節點 $1$ 開始，先往左子樹走，到了新子樹後到子樹根節點 $2$
接著又到新的左子樹根節點 $4$，此時對於根節點為 $2$ 的子樹來說左子樹已經結束了
所以輪到右子樹根節點 $5$，根節點為 $2$ 的子樹完全結束，所以輪到整棵樹的右子樹
右子樹根節點 $3$，然後整棵樹結束，前序就會是 $1,2,4,5,3$
從這個範例可以看出來，一顆二元樹的前三種遍歷順序都是唯一的，這時候就要反過來思考
用一個遍歷順序可以決定唯一的二元樹嗎 答案是"不行"
因為二元樹我們很清楚知道哪裡是根，哪裡是左子樹，哪裡是右子樹
但是順序(比如前序)只有講要先處理根，再處理左子樹，最後是右子樹
我們並不能區分哪些部分是左/右子樹，比如上面的例子前序: $1,2,4,5,3$
也可以是根為 $1$，然後一直往左子樹分支，最後圖是右上到左下的一直線，右上是根 $1$，左下是葉 $3$
其實要重建非常簡單，用中序+任意序列就可以組成唯一的二元樹
因為前序、後序可以馬上知道根，前序的根就在最左邊，後序的根就在最右邊
這時候就可以用類似移植的方法，以下是前序+中序的作法
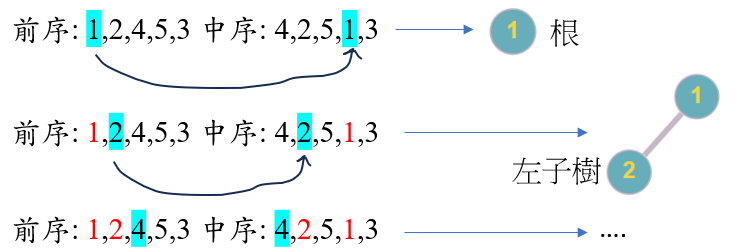
實際的程式邏輯也很簡單，就是先找出整顆樹的根，然後在定位中序裡根的位置 $PR$
假設 $PR$ 左方還有數字，根據中序"左子樹、根、右子樹"的順序，那些數字就是左子樹的節點
若左方已經沒有數字了，代表輪到右子樹了，跟左子樹的邏輯相似，右方數字代表右子樹節點
整個過程最重要的地方就是確立子樹的範圍與位置，拿剛剛的圖片例子來說明(簡易自己跟著做)
假設二元樹叫 $T$，左子樹分別為 $L_1, L_2, ...$，右子樹分別為 $R_1, R_2, ...$，可疊加
先找到 $T$ 的根，$T$ 的範圍是整個中序，根為此時前序走到的數字(從頭開始走，節點 $1$)
中序節點 $1$ 的左方是左子樹 $L_1$，進到 $L_1$ 後，$L_1$ 範圍在中序數字 $4,2,5$
$L_1$ 的根節點為前序往前走的第二個數字(節點 $2$)，這時候節點 $2$ 左方還有數字
進到左子樹 $L_2$，根為前序往前走的第三個數字(節點 $4$)，此時左方已經沒有數字了
回到 $L_1$，$L_1$ 根與 $T$ 根之間還有數字，所以 $L_1$ 有右子樹 $L_1R_1$
進到 $L_1R_1$，根為前序往前走的第四個數字(節點 $5$)，此時左右方都沒有數字了
所以回到 $L_1$，$L_1$ 左右子樹都走完了，所以回到 $T$，$T$ 右方還有數字，有右子樹 $R_1$
進到 $R_1$，根為節點 $3$，左右方都沒有剩餘數字了，所以直接回到 $T$，那整個 $T$ 就結束了
經過這個例子應該能很清楚知道，只有搭配中序才能知道子樹範圍，而其他順序則是提供每個子樹的根
以下是假設輸入前後任一順序+中序來建構唯一二元樹的程式碼

#include<bits/stdc++.h>
using namespace std ;

struct node {
    int val ;
    node* left ;
    node* right ;
};

void input_s(int m, string &s1, string &s2, string &s3) {
    if (m == 1) cin >> s1 ;
    else if (m == 2) cin >> s2 ;
    else cin >> s3 ;
    return ;
}

node* pre_con(string &pre, string &in, int* pidx, int s, int e) {
    if (s > e) return NULL ;
    int ridx = s, root = pre[(*pidx)++] ;
    while (in[ridx] != root) ridx++ ; // find root index

    node* now = new node ; // make root
    now->val = root-'0' ;
    now->left = pre_con(pre, in, pidx, s, ridx-1) ; // left tree
    now->right = pre_con(pre, in, pidx, ridx+1, e) ; // right tree
    return now ;
}

node* post_con(string &post, string &in, int* pidx, int s, int e) {
    if (s > e) return NULL ;
    int ridx = s, root = post[(*pidx)--] ;
    while (in[ridx] != root) ridx++ ; // find root index

    node* now = new node ; // make root
    now->val = root-'0' ;
    now->right = post_con(post, in, pidx, ridx+1, e) ; // right tree
    now->left = post_con(post, in, pidx, s, ridx-1) ; // left tree
    return now ;
}

node* make_tree(int m, string &pre, string &in, string &post) {
    int pidx, s = 0, e = in.size()-1 ;
    if (m == 1) {
        pidx = s ;
        return pre_con(pre, in, &pidx, s, e) ;
    }
    // else
    pidx = e ;
    return post_con(post, in, &pidx, s, e) ;
}

int main() {
    int m1, m2 ; // mode: 1->pre, 2->in, 3->post
    cin >> m1 >> m2 ;
    string s1, s2, s3 ;

    input_s(m1, s1, s2, s3) ;
    input_s(m2, s1, s2, s3) ;

    int m = m1+m2-2 ; // "1 or 3"+2(in)-2 -> make sure mode is 1 or 3
    node* root = make_tree(m, s1, s2, s3) ;

    // use bfs to show tree
    queue<node*> que ;
    que.push(root) ;

    while (!que.empty()) {
        node* now = que.front() ;
        que.pop() ;

        cout << "root " << now->val << ": " ;
        if (now->left != NULL) {
            que.push(now->left) ;
            cout << now->left->val << ' ' ;
        }
        if (now->right != NULL) {
            que.push(now->right) ;
            cout << now->right->val << ' ' ;
        }
        cout << '\n' ;
    }
    return 0 ;
}

以上實作只適用於節點 $0\sim 9$，也有很多的改進地方，但本來就只是講述概念而用
實際在解題過程中需依據題目給定的敘述與輸入去調整

---
層序也可以搭配中序來建構唯一二元樹，因為層序中父節點一定在子節點前方，不過不重要就不說明了

## 二元樹應用-(逆)波藍表示法
二元樹其實也可以用來表示四則運算，此時前序、後序就會對應到波蘭/逆波蘭
比如: $(1-2+3) \times (8+4\div 2)$，這個時候圖就會像是下面這樣
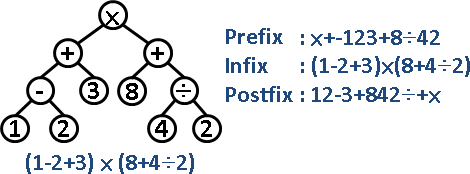
當然如果只是需要將四則運算改成(逆)波蘭表示法，並不需要建構二元樹，只需要使用 stack 就好
因為(逆)波蘭表示法不需要考慮先加減後乘除，也不需要考慮括號(都依順序排好了)
所以電腦實際在計算的時候大部分使用逆波蘭表示法，而其中的轉換是由編譯器處理的
不過這裡不會講太多，(逆)波蘭表示法的實作，或是四則運算的轉換等等都在 [stack 講義](/HJuDDdl21g)

## 二元樹應用-對稱樹(鏡像樹)
就是將二元樹照鏡子，鏡子左右兩側的樹會以鏡子為中心軸對稱(也就是節點、邊對稱)
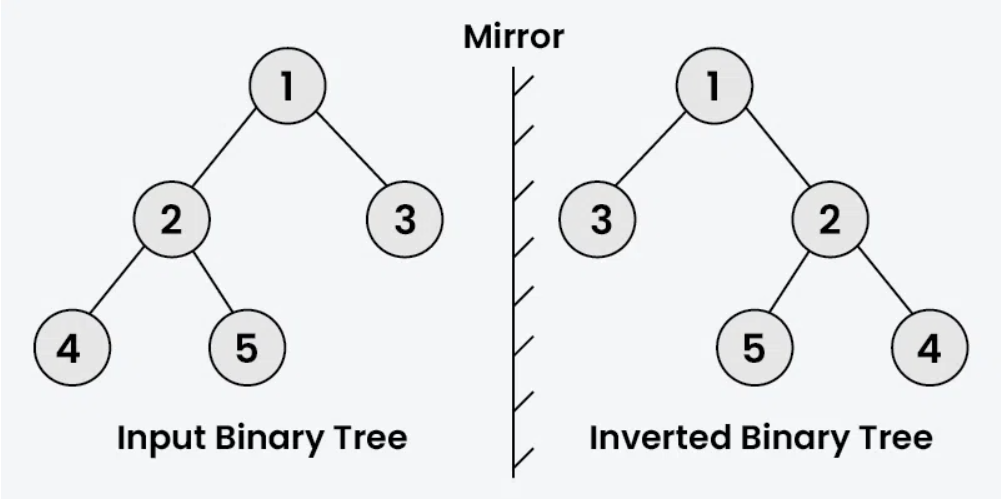
其實可以先從根節點來看，左節點需要變成右節點，右節點需要變成左節點
其他點也是這樣，所以應該是左右子樹互換，實際的程式碼會使用遞迴，如下

#include<bits/stdc++.h>
using namespace std ;

struct node {
    int val ;
    node* left ;
    node* right ;
};

int cal_node(int n) { // calculate max node num
    int num = 1 ;
    while (n) {
        n /= 2 ;
        num *= 2 ;
    }
    return num ;
}

node* make_tree(vector<int> &T, int idx, int n) { // array to tree
    if (idx > n) return NULL ;
    node* now = new node ;
    now->val = T[idx] ;
    now->left = make_tree(T, idx*2, n) ;
    now->right = make_tree(T, idx*2+1, n) ;

    return now ;
}

node* mirrow(node* root) {
    if (root == NULL) return NULL ;

    // 左右子樹對調
    node* L = mirrow(root->left) ;
    node* R = mirrow(root->right) ;
    root->left = R ;
    root->right = L ;
    return root ;
}

// tree to array
void tree_make_array(vector<int> &ans, node* nd, int idx) {
    if (nd == NULL) return ;
    ans[idx] = nd->val ;
    tree_make_array(ans, nd->left, idx*2) ;
    tree_make_array(ans, nd->right, idx*2+1) ;
}

int main() {
    ios::sync_with_stdio(0), cin.tie(0) ;

    int n ;
    cin >> n ;
    vector<int> T(n+1, 0) ;
    for (int i=1;i<=n;i++)
        cin >> T[i] ;

    node* root = new node ;
    root->val = T[1] ;
    root->left = make_tree(T, 2, n) ;
    root->right = make_tree(T, 3, n) ;

    mirrow(root) ;

    int num = cal_node(n) ;
    vector<int> ans(num, -1) ;
    tree_make_array(ans, root, 1) ;
    for (int i=1;i<num;i++) // show ans
        cout << ans[i] << ' ' ;
    cout << '\n' ;

    return 0 ;
}

但如果只是使用 array 去存，可以用一層層去對稱，程式碼如下

#include<bits/stdc++.h>
using namespace std ;

int cal_node(int n) { // calculate max node num
    int num = 1 ;
    while (n) {
        n /= 2 ;
        num *= 2 ;
    }
    return num ;
}

void mirrow(vector<int> &T, vector<int> &ans, int num, int n) {
    int times = 2, btimes = 1 ;

    while (times <= num) { // lvl 1 -> lvl 2 -> ...
        for (int i=0;i<btimes;i++) {
            if (btimes+i > n) // NULL node
                ans[times-1-i] = -1 ;
            else               // mirrow
                ans[times-1-i] = T[btimes+i] ;
        }
        btimes = times ;
        times *= 2 ;
    }
    return ;
}

int main() {
    ios::sync_with_stdio(0), cin.tie(0) ;

    int n ;
    cin >> n ;
    vector<int> T(n+1, 0) ;
    for (int i=1;i<=n;i++)
        cin >> T[i] ;

    int num = cal_node(n) ;
    vector<int> ans(num) ;

    mirrow(T, ans, num, n) ;
    for (int i=1;i<num;i++) // show ans
        cout << ans[i] << ' ' ;
    cout << '\n' ;

    return 0 ;
}

## 二元樹應用-堆積(Heap)
堆積是一種特殊的完全二元樹，通常用陣列來實作，主要分為 Max-Heap 和 Min-Heap
Max-Heap 的定義是任一節點的值都 $\ge$ 其子節點的值，與之相反的
Min-Heap 的定義是任一節點的值都 $\le$ 其子節點的值
Heap 可以實作之後會講到的 Priority Queue (優先佇列)，和排序、最短路等等
這裡只會簡單介紹一下實作的方法與二元樹的關係，還有提到 heap sort
建構 heap 要追朔到使用 array 表示二元樹，前面有說過就不重複，以下是 Max-Heap 的實作

#include<bits/stdc++.h>
using namespace std ;

struct Heap {
    int* hp ;  // array of heap
    int hsize ; // heap max size
    int hcount ; // heap element count
};

Heap* createHeap(int hsize) {
    Heap* h = new Heap ;
    h->hp = new int[hsize+1] ; // node index from 1 ~ hsiz
    h->hsize = hsize ;
    h->hcount = 0 ;
    return h ;
}

void insert_Heap(Heap* h, int value) {
    if (h->hcount >= h->hsize) return ;

    // 插入資料
    h->hcount++ ;
    h->hp[h->hcount] = value ;

    int idx = h->hcount ;

    // 檢查父節點是否較小->交換->重複檢查...
    while (idx > 1 && h->hp[idx] > h->hp[idx/2]) {
        int tmp = h->hp[idx] ;
        h->hp[idx] = h->hp[idx/2] ;
        h->hp[idx/2] = tmp ;
        idx /= 2 ;
    }
    return ;
}

void remove_top(Heap *h) {
    if (h->hcount == 0) return ;
    h->hp[1] = h->hp[h->hcount] ;
    h->hcount-- ;
    int idx = 1 ;
    while (true) {
        int maxPos = idx ;
        // 左子節點判斷(沒超出範圍且較大)
        if (2*idx <= h->hcount && h->hp[2*idx] > h->hp[maxPos])
            maxPos = 2*idx ;
        // 右子節點判斷(沒超出範圍且較大)
        if (2*idx+1 <= h->hcount && h->hp[2*idx+1] > h->hp[maxPos])
            maxPos = 2*idx+1 ;
        if (maxPos == idx) break ; // max element

        int tmp = h->hp[idx] ;
        h->hp[idx] = h->hp[maxPos] ;
        h->hp[maxPos] = tmp ;
        idx = maxPos ;
    }
    return ;
}

int get_max(Heap* h) {
    return h->hp[1] ;
}

int main() {
//    ios::sync_with_stdio(0), cin.tie(0) ;

    Heap* h = createHeap(10) ; // a heap of size of 10
    insert_Heap(h, 20) ;
    insert_Heap(h, 15) ;
    insert_Heap(h, 25) ;
    insert_Heap(h, 30) ;
    insert_Heap(h, 10) ;
    insert_Heap(h, 5) ;
    cout << "The top(maximum) is " << get_max(h) << '\n' ;
    remove_top(h) ;
    cout << "The top(maximum) is " << get_max(h) << '\n' ;
    return 0 ;
}

從上面的程式碼應該可以得知基礎的 heap 就是保持某個最大(小)值在樹的根節點
以最大值在樹根舉例，兩個子節點一定有一個是第二大的節點，可以用反證法去推
假設第二大的節點不是那兩個節點，那一定在那兩個節點的子樹當中，而根節點一定大於子孫節點
所以假設不成立，因此根節點的兩個子節點一定有一個是第二大的節點
所以在刪除最大值的時候，就是把根節點去除，然後找出第二大的節點去當根
原本第二大節點的子樹這時候也像是失去根節點一樣，重複執行直到走到葉節點

---
插入 heap、刪除頂點的時間複雜度都是 $O(log\ n)$，找出最大(小)值是 $O(1)$，因為直接看樹根就好
還有將二元樹轉換成 heap 的程式，時間複雜度是 $O(n)$，證明有點複雜，建議自行查詢
二元樹轉換成 heap 的程式碼跟 heap sort 放在下方

void heapifyDown(Heap* h, int idx) { // 修復 heap 性質
    int largest = idx ;
    int l = 2*idx+0 ;
    int r = 2*idx+1 ;
    if (l < h->hcount && h->hp[l] > h->hp[largest]) largest = l ;
    if (r < h->hcount && h->hp[r] > h->hp[largest]) largest = r ;

    if (largest != idx) {
        swap(h->hp[idx], h->hp[largest]) ;
        heapifyDown(h, largest) ;
    }
    return ;
}

void buildHeap(Heap* h) { // 將 hp 轉換成 heap
    for (int i=h->hcount/2;i>=1;i--)
        heapifyDown(h, i) ;
    return ;
}

void heapSort(Heap* h) {
    buildHeap(h) ;  // 建構最大堆

    for (int i=h->hcount-1; i > 0; i--) {
        swap(h->hp[0], h->hp[i]) ;  // 將最大值移到尾端
        h->hcount-- ;               // 排除尾端元素
        heapifyDown(h, 0) ;             // 修復 heap 性質
    }
}

以上程式碼就是 Heap sort，簡單講就是用 Max-Heap 的特性(最大值在樹根)
然後把當前最大值跟最尾端(未排序)的值交換位置，所以最大值就會跑到最尾端
接著重複這個動作就可以讓所有的節點排好，因為 heap 本身就是 array 所以不需要額外空間
時間複雜度是 $O(nlog\ n)$，空間複雜度是 $O(1)$

## 二元樹應用-二元搜尋樹(BST)
BST 定義，對任意節點 $N$ 來說，左子樹的所有節點值都小於 $N$ 的值，右子樹是大於
以下做 BST 的插入、搜尋，還有依遞增順序輸出三個操作，刪除比較麻煩，就在之後的篇章講述了

#include<bits/stdc++.h>
using namespace std ;

struct node {
    int val ;
    node* left ;
    node* right ;
};

void insert_node(node* root, int val) { // insert
    node* now = new node ;
    now->val = val ;
    now->left = now->right = NULL ;
    while (true) {
        if (root->val > val && root->left == NULL) { // left tree
            root->left = now ;
            break ;
        }
        else if (root->val > val)
            root = root->left ;
        else if (root->val < val && root->right == NULL) { // right tree
            root->right = now ;
            break ;
        }
        else if (root->val < val)
            root = root->right ;
    }
    return ;
}

bool find_node(node* root, int val) {
    while (root != NULL) {
        if (root->val == val) return true ;
        if (root->val < val) root = root->right ; // right tree
        else if (root->val > val) root = root->left ; // left tree
    }
    return false ;
}

void print_node(node* root) {
    if (root->left != NULL) print_node(root->left) ;
    cout << root->val << ' ' ;
    if (root->right != NULL) print_node(root->right) ;
    return ;
}

int main() {
//    ios::sync_with_stdio(0), cin.tie(0) ;

    node* vroot = new node ; // 虛擬根
    vroot->val = INT_MAX ;
    vroot->left = vroot->right = NULL ;
    int n, x ;
    cin >> n ;
    for (int i=0;i<n;i++) {
        cin >> x ;
        insert_node(vroot, x) ;
    }

    int m ;
    cin >> m ;
    for (int i=0;i<m;i++) {
        cin >> x ;
        if (find_node(vroot, x))
            cout << x << " is in BST\n" ;
        else
            cout << x << " isn't in BST\n" ;
    }
    cout << "\n\n" ;

    print_node(vroot->left) ;
    return 0 ;
}

這裡用虛擬根(數值最大)作為一開始的樹，讓後面的建構變得比較簡單，還要注意左右節點是否存在
其實二分搜尋樹有更進階的實作，下面和之後的進階篇章都會講到
這裡只需要強調一個點，就是依照值大小輸出的概念，其實是中序
因為中序是輸出左節點-根-右節點，根據 BST 的定義來說，左節點一定比根小，右節點大

而二分搜尋樹最大的問題就是如果數字進入的順序呈現上升或下降趨勢(數字越來越大或越來越小)
那插入、查詢、刪除的效率會變得很差，因為樹會像是左上到右下一條鍊子，或是右上到左下
原本 $O(log\ n)$ 的操作會變成 $O(n)$，為了解決這個效率問題，我們要讓樹盡量平衡
所謂的平衡就是減少這種鏈式結構的出現，讓樹變成每一層都盡量把節點填滿，增加效率

### 二元搜尋樹進階-平衡二元搜尋樹(AVL Tree)
任一節點對應的兩棵子樹(左右子樹)的最大高度差為 $1$，因此也被稱為高度平衡樹
更明確的說法每個節點都有一個稱為**平衡因子**的屬性，為該點**左子樹高度減去右子樹高度**
而每個節點的平衡因子都必須介於 $-1\sim1$，平衡因子只能是 $-1、0、1$ 才能讓樹盡量平衡
當某個節點平衡因子超出範圍，那就需要做旋轉操作，讓樹回到平衡狀態，主要有四種旋轉
1. 左旋: 右子樹過高時使用
2. 右旋: 左子樹過高時使用
3. 左右旋: 左子樹的右子樹過高時使用，先將左方的子節點做左旋，在對當前節點做右旋
4. 右左旋: 右子樹的左子樹過高時使用，先將右方的子節點做右旋，在對當前節點做左旋

以下是程式碼範例

#include<bits/stdc++.h>
using namespace std ;

struct node {
    node* left ;
    node* right ;
    int val, h ; // h 子樹高度
};

node* make_node(int data) {
    node* now = new node ;
    now->val = data ;
    now->h = 1 ;
    now->left = now->right = NULL ;

    return now ;
}

int geth(node* nd) { // get height
    if (nd == NULL) return 0 ;

    return nd->h ;
}

int getbalance(node* nd) { // get balance
    if (nd == NULL) return 0 ;

    return geth(nd->left) - geth(nd->right) ;
}

node* rightRotate(node* nd) { // 右旋
    node* ndL = nd->left ;
    node* ndLR = ndL->right ;
    ndL->right = nd ;
    nd->left = ndLR ;

    nd->h = max(geth(nd->left), geth(nd->right)) + 1 ;
    ndL->h = max(geth(ndL->left), geth(ndL->right)) + 1 ;
    return ndL ;
}

node* leftRotate(node* nd) { // 左旋
    node* ndR = nd->right ;
    node* ndRL = ndR->left ;
    ndR->left = nd ;
    nd->right = ndRL ;
    
    nd->h = max(geth(nd->left), geth(nd->right)) + 1 ;
    ndR->h = max(geth(ndR->left), geth(ndR->right)) + 1 ;
    return ndR ;
}

// insert to nd left or right, if nd is NULL, let nd be new node
node* insert_node(node* nd, int data) {
    if (nd == NULL)
        return make_node(data) ;

    if (data < nd->val)
        nd->left = insert_node(nd->left, data) ;
    else
        nd->right = insert_node(nd->right, data) ;

    // 更新樹高度
    nd->h = 1 + max(geth(nd->left), geth(nd->right)) ;

    // 判斷是否平衡->四種平衡處理
    int balance = getbalance(nd) ; // 平衡因子
    if (balance > 1 && data < nd->left->val)
        return rightRotate(nd) ;
    if (balance < -1 && data > nd->right->val)
        return leftRotate(nd) ;
    if (balance > 1 && data > nd->left->val) {
        nd->left = leftRotate(nd->left) ;
        return rightRotate(nd) ;
    }
    if (balance < -1 && data < nd->right->val) {
        nd->right = rightRotate(nd->right) ;
        return leftRotate(nd) ;
    }
    return nd ;
}

node* min_node(node* nd) {
    node* cur = nd ;
    while(cur->left != NULL)
        cur = cur->left ;
    return cur ;
}

node* delete_node(node* root, int data) {
    if (root == NULL)
        return root ;
    if (data < root->val)
        root->left = delete_node(root->left, data) ;
    else if (data > root->val)
        root->right = delete_node(root->right, data) ;
    else {
        if (root->left == NULL || root->right == NULL) {
            node* tmp = root->left ? root->left : root->right ;
            if (tmp == NULL) { // left, right all NULL
                tmp = root ;
                root = NULL ;
            }
            else
                *root = *tmp ;
            delete tmp ;
        }
        else {
            node* tmp = min_node(root->right) ;
            root->val = tmp->val ;
            root->right = delete_node(root->right, tmp->val) ;
        }
    }

    if (root == NULL)
        return NULL ;

    // 更新高度
    root->h = 1 + max(geth(root->left), geth(root->right)) ;
    
    // delete 平衡
    int balance = getbalance(root) ;
    if (balance > 1 && getbalance(root->left) >= 0) {
        return rightRotate(root) ;
    }
    if (balance > 1 && getbalance(root->left) < 0) {
        root->left = leftRotate(root->left) ;
        return rightRotate(root) ;
    }
    if (balance < -1 && getbalance(root->right) <= 0) {
        return leftRotate(root) ;
    }
    if (balance < -1 && getbalance(root->right) > 0) {
        root->right = rightRotate(root->right) ;
        return leftRotate(root) ;
    }
    return root ;
}

void print_node(node *root) { // 依值大小輸出
    if(root != NULL) {
        print_node(root->left) ;
        printf("%d ", root->val) ;
        print_node(root->right) ;
    }
}

int main() {
    ios::sync_with_stdio(0), cin.tie(0) ;

    node* root = NULL ;
    int n, x ;
    cin >> n ;
    for (int i=0;i<n;i++) {
        cin >> x ;
        root = insert_node(root, x) ;
    }
    print_node(root) ;
    printf("\n") ;

    // 刪除節點 20
    root = delete_node(root, 20) ;
    print_node(root) ;
    printf("\n") ;

    return 0 ;
}

這棵樹的插入、刪除、查詢的時間複雜度都是 $O(log\ n)$
但有些平衡操作還是比較耗時的，所以在大量修改節點的情況下，會選擇其他平衡樹
這裡只是平衡樹的前瞻，更詳細的應用就等到後面的篇章再說

## n 元樹簡述
$n$ 元樹是由二元樹拓展而來的，名稱有很多，包含: 多元樹，n-ary tree，k-way tree
從名稱上也可以知道，每個節點最少是 $0$ 個子節點，最多可以有 $n$ 個子節點
其實應該看的出來，這個基本上就是原來的樹，所有的樹不過就是二元樹的拓展、轉化、變形
而 $n$ 元樹的存法就跟前面提到的一樣，甚至在二元樹之後我們還能知道以下方法也是可行的

struct node {
    int val ;
    node* parent ;
    vector<node*> sub_node ;
};

當然，將 $n$ 元樹回歸成二元樹也可以，就是把多出來的子節點放到第一個子節點的右子樹
而第一個子節點放到原父節點的左子樹，直接看例子會比較快
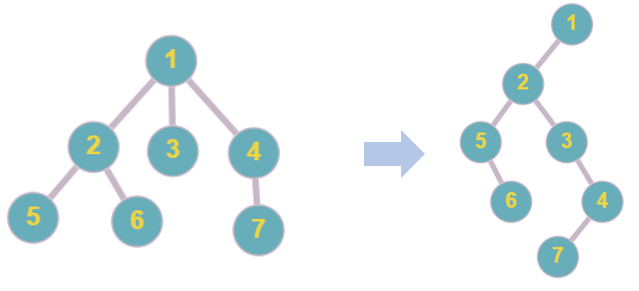
首先就是根不會變動，所以節點 $1$ 直接移過去，然後找出節點 $1$ 的第一個子節點 $2$
$2$ 的右子樹會連結著與 $2$ 同父節點的節點，所以 $3$ 會是 $2$ 的右節點
同理，節點 $4$ 會是 $3$ 的右節點，然後 $2$ 的子節點會在 $2$ 的左子樹
跟剛剛一樣，節點 $5$ 是 $2$ 的左節點，節點 $6$ 是 $5$ 的右節點
最後節點 $7$ 是 $4$ 的左節點，整顆二元樹就完成了，實際上的順序可能跟我敘述的不同