###### tags: `school`

資料結構與演算法
===

神秘的資料結構與演算法，例子都是C語言

森哥必考題，資料結構是甚麼，以下開放作答

期末考
===

樹
---

### 二元樹

一個樹如果每個節點都有兩個子節點就叫做二元樹

- 完整(Complete)二元樹
- 靠左中間沒有空隙的樹就是完整二元樹
- 高度是$lg(n) + 1$，n是節點數量
- 節點個數$2^{k-1} \le n \le 2^K - 1$，k是樹的高度
- 完滿(full)二元樹
- 如果每一層的節點不是0就是$2^k$就是完滿二元樹
- 是完整二元樹的子集

### 二元樹走訪


前序:

1,2,4,7,8,5,3,6,9,10

中序:

7,4,8,2,5,1,3,9,6,10

後序:

7,8,4,5,2,9,10,6,3,1

### 二元搜尋樹

對所有節點來說，他左子樹的所有節點都小於他，他右子樹的所有節點都大於他，中序走訪一下就是二元樹排序了

建立就是比大小

要刪除節點不知道怎麼刪就中序跑一遍，把列表裡的前一個節點或後一個節點拿來頂就好了

### B樹

> 森哥在想甚麼你心裡沒點B樹嗎

這個到底有沒有教阿，我沒印象森哥講過

### 霍夫曼樹(Huffman Tree)

> 大概會考如何編碼跟算壓縮率

假設有以下字母與出現次數

| Letter | Frequency |
| ------ | --------- |
| Z | 2 |
| K | 7 |
| M | 24 |
| C | 32 |
| U | 37 |
| D | 42 |
| L | 42 |
| E | 120 |

把最小的兩個拉出來弄成一個小樹，數值為兩人相加，如次往復

> 因為阿寶懂了，所以我就不寫清楚了


樹建完後的編碼與字母表為

| Letter | Code | bit |
| ------ | ------ | --- |
| E | 0 | 1 |
| U | 100 | 3 |
| D | 101 | 3 |
| L | 110 | 3 |
| C | 1110 | 4 |
| M | 11111 | 5 |
| Z | 111100 | 6 |
| K | 111101 | 6 |

原本的文件大小是8 bit乘上所有字母出現的次數，也就是8 * 306 = 2448

壓縮後的文件為

1 * 120 + 3 * 37 + 3 * 42 + 3 * 37 + 4 * 32 + 5 * 24 + 6 * 2 + 6 * 7 = 770

壓縮率是1 - 770/2448 = 68.54%

可能還會考編碼跟解碼，編碼很簡單，照填就好，解碼就是看著樹走，走到有字母的地方就分一群出來

111111001110111101 => 11111 100 1110 111101 => MUCK

排序
---

> 除了合併、快速、heap沒啥好講的

### Merge Sort


### Quick Sort


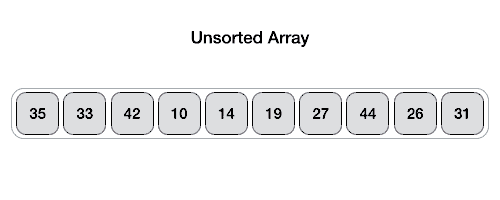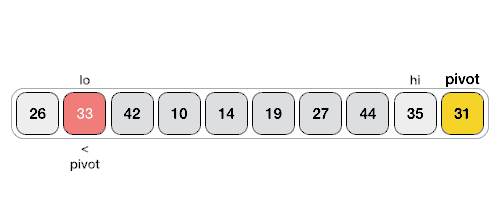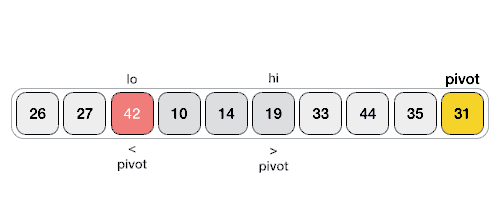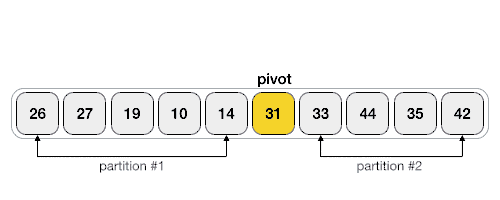
### Heap Sort


搜尋
---

> 二分很直覺，內差背公式，hash靠天分

期末考不考的選讀-(少_06/17_18:30)
---

> 這些全憑我的印象，歡迎增刪

- 第六章-樹
- P.6-23 引線二元素
- P.6-40 高度平衡樹/AVL樹
- P.6-46 m元搜尋樹
- 第七章-排序
- Shell
- 基數
- 第八章-搜尋
- P.8-13 費氏搜尋
- P.8-31 可擴充雜湊

期中考
===

資料結構是甚麼
---

- 路西
- 資料的儲存方式
- 少廷
- 把資料以便於演算法處理的方式組織並儲存的結構方式。

Big-O是甚麼
---

- 路西
- 函數中變數的增長對函數增長速度的上限
- 少廷
- 為表示時間複雜度用來判斷演算法執行快慢的常用上限符號。
- (維基)它是用另一個函式來描述一個函式數量級的漸近上界，是描述函數漸進行為的常用符號。

必考題列表
---

- 資料結構是甚麼
- 前序後序
- BIGO是甚麼
- 手寫程式碼
- Ackermann
- Array Address
- Graph Traversal
- BFS
- DFS
- Minimum Spanning Tree
- Kruskal
- Prim
- Shortest Path
- Dijkstra
- ~~Floyd~~ (好像還沒教到)

將程式的複雜程度量化
===

要比較程式的好壞就需要能夠將程式的複雜程度數值化，我們才能夠用數學方法比較其優劣，其中最常用的是Big-O

> 雖然其實很多人說Big-O時指的其實是Big-$\Theta$

Big-O的精確數學定義是

$$
Def: f(n) = O(g(n))
$$

$$
\exists \; c,n_0 \ni |f(n)| \le c|g(n)| \quad \forall n \ge n_0
$$

### 白話文翻譯

有兩個函數$f$和$g$，如果存在兩個數字$c$和$n_0$讓所有大於等於$n_0$的$n$都讓上面的不等式成立，則$g$就是$f$的Big-O

### 例子

先來設定$f$

$$
f = 5n^2 + 1 \\
$$

接著猜一個$g$

$$
g = n^2
$$

要證明$f(n) = O(g(n))$我們就要找出能否有$c$跟$n_0$存在

我們可以看出$f$裡最高的係數是5，那我們就可以把$c$設成6，然後看一下把$n$帶數字進去是多少

| $n$ | $\mid f(n) \mid$ | $c\mid{g(n)}\mid$ |
| --- | ---------------- | ----------------- |
| 0 | 1 | 0 |
| 1 | 6 | 6 |
| 2 | 21 | 24 |

可以看出當$n = 2$時不等式就成立了，並且類推下去都是成立的，因為1的影響力跟平方相比太小了，所以可以證明

$$
5n^2 + 1 = O(n^2)
$$

如果當初我們$g$選錯就無法產生這種結果，那怕$c$再大都沒有用

$$
g = n, c = 100
$$

| $n$ | $\mid f(n) \mid$ | $c\mid{g(n)}\mid$ |
| --- | ---------------- | ----------------- |
| 0 | 1 | 0 |
| 1 | 6 | 100 |
| 2 | 21 | 200 |
| 10 | 501 | 1000 |
| 20 | 2001 | 2000 |
| 100 | 50001 | 10000 |

可以看出當$n = 20$的時候$c$就沒用了，並且後面不等式都不會成立，後續不等式的嚴謹證明要透過極限運算這邊就不寫了

### 結論

從上面的例子可以看出Big-O所計算出的是一個函數的上界，並且我們知道了$n < n^2$，所以當我們將程式執行的次數轉成函數時就可以透過Big-O來得知當資料量很大時程式之間相對的優劣

> 因為Big-O是上界，所以其實$n^2 = O(n^3)$也是成立的，但是這樣寫小心被森哥打錯

接著我們來把一些程式的執行次數轉成函數看看，以下例子中假設程式最花時間執行的部分是加法運算

以下皆會在程式碼前標註執行次數和Big-O

$1 = O(1)$

#include <stdio.h>

int main(void){
    
    int x = 0;
    
    x++; //x最後等於1

    return 0;
}

$3 = O(1)$

int main(void){

    x++;
    x++;
    x++; //x最後等於3

    return 0;
}

$n = O(n)$

#include <stdio.h>

int main(void){

    int n = 10; //請把這個n當成資料量
    
    int x = 0;
    int i;
    
    for(i = 0;i < n;i++){ //for迴圈會跑n次
        x++; //x = n
    }

    return 0;
}

$n^2= O(n^2)$

#include <stdio.h>

int main(void){

    int n = 10; //請把這個n當成資料量
    
    int x = 0;
    int i,j;
    
    for(i = 0;i < n;i++){ //for迴圈會跑n次
        for(j = 0;j < n;i++){ //for迴圈會跑n次
            x++; //x = n^2
        }
    }

    return 0;
}

$\sum_{k = 1}^{n} k = 1 + 2 + ... + n = \frac{n(1+n)}{2} = O(n^2)$

#include <stdio.h>

int main(void){

    int n = 10; //請把這個n當成資料量
    
    int x;
    int i, j;
    
    for(i = 0;i < n;i++){ //for迴圈會跑n次
        for(j = i;j < n;i++){ //for迴圈會跑n - i次
            x++; // 
        }
    }

    return 0;
}

迴圈的其他種變體就回憶一下等差數列就會算了

這邊簡單的列一下Big-O的大小

$$
O(1) < O(log(n)) < O(n) < O(log(n) * n) < O(n^2) < O(n!) < O(n^n)
$$

### 小題目

證明

$$
n! = O(n^n)
$$

\begin{split}
n! &= 1 * 2 * ... * n \\
n! &\le n * n * ... * n \\
n! &\le n^n \\
n! &= O(n^n) \\
\end{split}

基礎資料結構
===

最基本的資料結構有兩種，陣列(array)跟鏈結串列(linked list)，之後幾乎不論何種資料型態都是用這兩種資料型態為基底實作的

陣列(array)
---

陣列在C中為基本的資料型態，運作方式是把記憶體割一塊連續的部分用，因為是連續的記憶體所以在知道要找的資料是第幾筆的時候可以直接透過四則運算知道

### 程式碼範例

在C裡可以直接把記憶體位置顯示出來看

#include <stdio.h>

int main() {
    int a[100]; //宣告空間大小能夠放下100個int的陣列

    int i;

    for(i = 0;i < 100;i++){
        a[i] = i * i;
    }

    printf("%p:%d\n", &a[0], a[0]);
    printf("%p:%d\n", &a[50], a[50]);
}

上面的例子每台電腦的執行結果應該不太一樣，我的執行結果是

0x7ffd84604580:0
0x7ffd84604648:2500

前面是記憶體位址，後面是陣列內存放的數值，記憶體位址開頭的0x代表這串數字是十六進位表示的，換成十進位就是

140726824355200:0
140726824355400:2500

可以看出兩個位址間剛好差了200，那是因為c中int的大小是4 byte，也就是a[50]的位址就是a[0]的位址加上50(index)乘以4(資料大小)

> 如果你的處理器是16位元的話int大小就會是2 byte

這邊我們可以換個資料型態試試看

#include <stdio.h>

int main() {
    char a[100]; //雖然char是存字元用的，但是也可以拿來存1 byte的整數

    int i;

    for(i = 0;i < 100;i++){
        a[i] = i; //1 byte 最多只能放到255，就不虐待它了 
    }

    printf("%p:%d\n", &a[0], a[0]);
    printf("%p:%d\n", &a[50], a[50]);
}

執行結果是

0x7ffec9df81d0:0
0x7ffec9df8202:50

一樣轉換一下

140732285288912:0
140732285288962:50

可以看出就是普通的差了50，因為char的大小是1 byte

> 如果不想轉換的話可以把printf中的%p改成%d，就能直接得到十進位囉，只是會被編譯器罵就是了

### 陣列的操作

從上面的例子可以看出陣列取值很快，時間複雜度(也就是Big-O)是$O(1)$，不論你的陣列多大取值的速度都不會有太大變化

但是當要對陣列進行插入或會導致資料位移的操作時就很慢了，因為array必須將所有資料移往下一格，所以時間複雜度是$O(n)$，其中n是資料量

鏈結串列(linked list)
---

放置鋪類

堆疊(stack)與佇列(queue)
===

放置鋪類

運算式
---

人類平常使用的運算式都是將運算符(就加減乘除)放在中間做運算，這種方式稱為中序式，但對程式而言解析中序式比較麻煩，如果將中序式轉為前序式或後序式再解析程式就會好寫很多

### 人工轉換

設我們的算式為

$$
a + b * d + c / d
$$

根據先乘除後加減可以加上框框

$$
((a + (b * d)) + (c / d))
$$

如果轉成前序式就是先把最先執行的括號內的符號移到前面，並拿掉括號，如此重複

$$
((a + *bd) + /cd))
$$

$$
(+a*bd + /cd)
$$

$$
++a*bd/cd
$$

後序式

$$
((a + bd*) + cd/)
$$

$$
(abd*+ + cd/)
$$

$$
abd*+cd/+
$$

### 程式轉換

> 好像沒有要考，放著

### 轉換後運算

> 好像也沒有要考

中序式為

$$
(8 + 2) * 5 - 6 / 3 = 48
$$

後序式為

$$
82+5*63/-
$$

計算過程如下

| symbol stack | number stack | seek |
| ------------ | ------------ | ---- |
| | 8 | 8 |
| | 8 2 | 2 |
| + | 8 2 | + |
| | 10 5 | 5 |
| * | 10 5 | * |
| | 50 6 | 6 |
| | 50 6 3 | 3 |
| / | 50 6 3 | / |
| - | 50 2 | - |
| | 48 | \0 |

前序式為

$$
-*+825/63
$$

| symbol stack | number stack | seek |
| ------------ | ------------ | ---- |
| - | | - |
| - * | | * |
| - * + | | + |
| - * + | 8 | 8 |
| - * + | 8 2 | 2 |
| - * | 10 5 | 5 |
| - / | 50 | / |
| - / | 50 6 | 6 |
| - / | 50 6 3 | 3 |
| - | 50 2 | \0 |
| - | 48 | \0 |

遞迴
---

### Ackermann

函數定義

\begin{equation}
A(m,n) = \left\{\begin{array}{ll}
n + 1, & \mbox{if $m = 0$} \\
A(m-1, 1), & \mbox{if $m > 0,n = 0$} \\
A(m-1, A(m, n-1)), & \mbox{otherwise.}
\end{array} \right.
\end{equation}

程式碼

#include <stdio.h>

//函式本體
int ackermann(int m, int n){
    if(m == 0) return n + 1;
    if(n == 0) return ackermann(m-1, 1);

    return ackermann(m - 1, ackermann(m, n - 1));
}

//顯示0到3的可能性
int main(void){

    int i, j;

    for(i = 0;i < 4;i++){
        for(j = 0;j < 4;j++){
            printf("%d \t", ackermann(i, j));
        }

        printf("\n");
    }

    return 0;
}

[線上測試](https://repl.it/@alan8365/Ctest)

圖(graph)
===

Graph Traversal
---

### 廣度優先搜尋(BFS)

> 森哥要哪種阿


| visited set | visit queue |
| ------------------------- | ----------- |
| | A |
| A | B, C, D |
| A, B | C, D, E |
| A, B, C | D, E, F, G |
| A, B, C, D | E, F, G, H |
| A, B, C, D, E | F, G, H |
| A, B, C, D, E, F | G, H, I |
| A, B, C, D, E, F, G | H, I |
| A, B, C, D, E, F, G, H | I |
| A, B, C, D, E, F, G, H, I | |

### DFS


| visited set | visit stack |
| ----------------- | ----------- |
| | A |
| A | B C D |
| A D | B C H |
| A D H | B C G |
| A D H G | B C I |
| A D H G I | B C F |
| A D H G I F | B C E |
| A D H G I F E | B C |
| A D H G I F E C | B |
| A D H G I F E C B | |

Minimum Spanning Tree
---

### Kruskal

[來源](http://alrightchiu.github.io/SecondRound/minimum-spanning-treekruskals-algorithm.html)


先將邊排序


接著從最小的邊開始加入，並將會形成迴路的邊忽略




1-6這條邊會形成迴路，所以忽略





這樣就完成了

### Prim

[來源](http://alrightchiu.github.io/SecondRound/minimum-spanning-treeprims-algorithm.html)

prim演算法需要三個大小n的陣列

predecessor代表某個節點的前一個節點是誰，-1代表還沒有找過
key代表從predecesso到某個節點的權重，預設無限
visited代表某個節點有沒有被加入結果內，0代表沒有1代表有


首先我們要找一個起點，這邊我們挑2當作起點，因為2被加入最終結果了所以visited改成1，並且到達2的權重為1


再來將與2相連的所有節點的權重與key相比，如果比key小就加入並將predecessor改成2


接著把key中最小的且visited不是1的加入結果，並把visited改成1


底下以此類推









Shortest Path
---

### Dijkstra

! [](https://i.imgur.com/JYJksko.png)

| Decided vertices | $v_1$ | $v_2$ | $v_3$ | $v_4$ | $v_5$ |
|:-----------------------:| ------- | ---------- | ---------- | ---------- | ------- |
| {$v_0$} | 8/0 | $\infty$/0 | $\infty$/0 | $\infty$/0 | **1/0** |
| {$v_0,v_5$} | 8/0 | $\infty$/0 | **3/5** | 9/5 | |
| {$v_0,v_5,v_3$} | **7/3** | 9/3 | | 9/5 | |
| {$v_0,v_5,v_3,v_1$} | | **8/1** | | 9/5 | |
| {$v_0,v_5,v_3,v_1,v_2$} | | | | **9/5** | |

# Dark Theme CSS

{%hackmd theme-dark %}