# 2017q3 Homework1 (ternary)
contributed by `<jackyhobingo>`
### reviewed by `Jetudie`
+ 在 "Balanced Ternary 的設計要解決的問題類型" 中,已從空間使用效率去探討,但未詳述實際應用,缺乏呼應題目的結論:建議對於能解決問題的類型做個舉例。
+ 在 "想法 & 思考" 中:
+ "經由測試結果猜測","猜測"適用於測試之前無規則依循的時候,而此時已有測試及參考,可用"推測"。
+ 對測試出來的結果缺乏描述,建議把推測的想法過程表達出來。
+ 有 typo, 是四個邊四個"角"而非"腳",是依"照"而非"造"。
+ 四個邊角分別為$3^0, 3^1, 3^2$...未說明邊角的順序,表達可再更明確。
---
## Balanced Ternary 原理
### Ternary System
相較於一般常見 base2 的進位模式, Ternary System 是一種 base3 的進位系統。Ternary System 計算模式類似 binary system , [影片一](https://www.youtube.com/watch?v=vOyiHMa-mtQ)中舉 $45_{10}\to1200_{3}$ 為例子。
e.g.
$\quad45\div3=15\dots0$
$\quad15\div3=5\dots0$
$\quad5\div3=1\dots2$
$\quad2\div3=0\dots1$
$\quad1200_3=1\times3^3+2\times3^2+0\times3^3+0\times3^0=45_{10}$
### Balanced Ternary
Balanecd Ternary 是以 -, 0, + 表示的 Ternary System
可以用 $\sum\limits_{i}^{n}c_i3^i$ 來表示換算成十進位大小
e.g.
基本十進位與 Balanced Ternary 轉換例子
||$3^2$|$3^1$|$3^0$||
|-|-|-|-|-|
|$5$|$+$|$-$|$-$|$+1\times3^2-1\times3^1-1\times3^0=+9-3-1=5$|
|$-5$|$-$|$+$|$+$|$-1\times3^2+1\times3^1+1\times3^0=-9+3+1=-5$|
|$7$|$+$|$-$|$+$|$+1\times3^2-1\times3^1+1\times3^0=+9-3+1=7$|
|$-7$|$-$|$+$|$-$|$-1\times3^2+1\times3^1-1\times3^0=-9+3-1=-7$|
|$2$|$0$|$+$|$-$|$0\times3^2+1\times3^1-1\times3^0=0+3-1=2$|
### Balanced Ternary logic table
影片二提到一些 balanced ternary logic table
|sum|$-$|$0$|$+$|
|-|-|-|-|
|$-$|$+$|$-$|$0$|
|$0$|$-$|$0$|$+$|
|$+$|$0$|$+$|$-$|
|carry|$-$|$0$|$+$|
|-|-|-|-|
|$-$|$-$|$0$|$0$|
|$0$|$0$|$0$|$0$|
|$+$|$0$|$0$|$+$|
|$\times$|$-$|$0$|$+$|
|-|-|-|-|
|$-$|$+$|$0$|$-$|
|$0$|$0$|$0$|$0$|
|$+$|$-$|$0$|$+$|
|$\div$|$-$|$0$|$+$|
|-|-|-|-|
|$-$|$+$|$-\infty$|$-$|
|$0$|$0$|$NAN$|$0$|
|$+$|$-$|$\infty$|$+$|
### ternary multiplexer
在文章[Ternary computing: basics](https://github.com/ssloy/tutorials/wiki/Ternary-computing:-basics)中,設計一種 ternary 的多工器,如圖二,可以藉由 pin sel 來決定可以輸出哪一個 pin 的值,並且可以藉由設定 inN, inO, inP 值的不同來設計出如A+1, A-1, max(A,0), min(A,0) 不同 Function , 進而設計出半加器(圖三、圖四),再組合成全加器(圖五、圖六)。
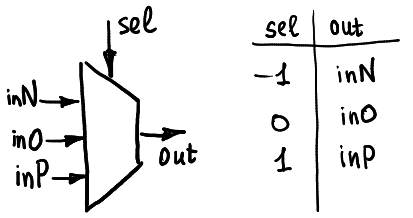
(圖二)
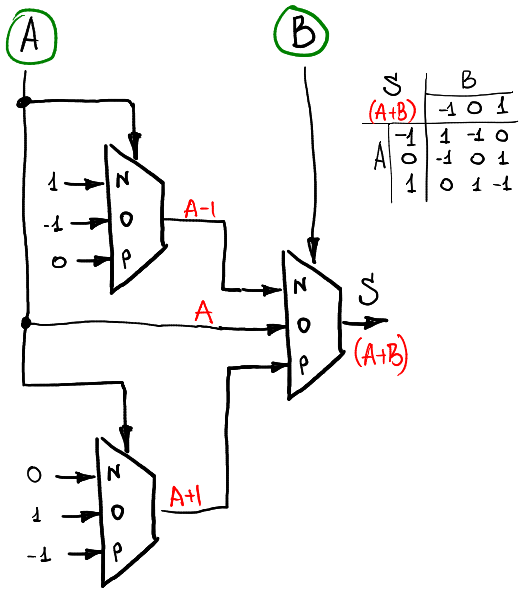
(圖三 半加器 S)
.png)
(圖四 半加器 C)
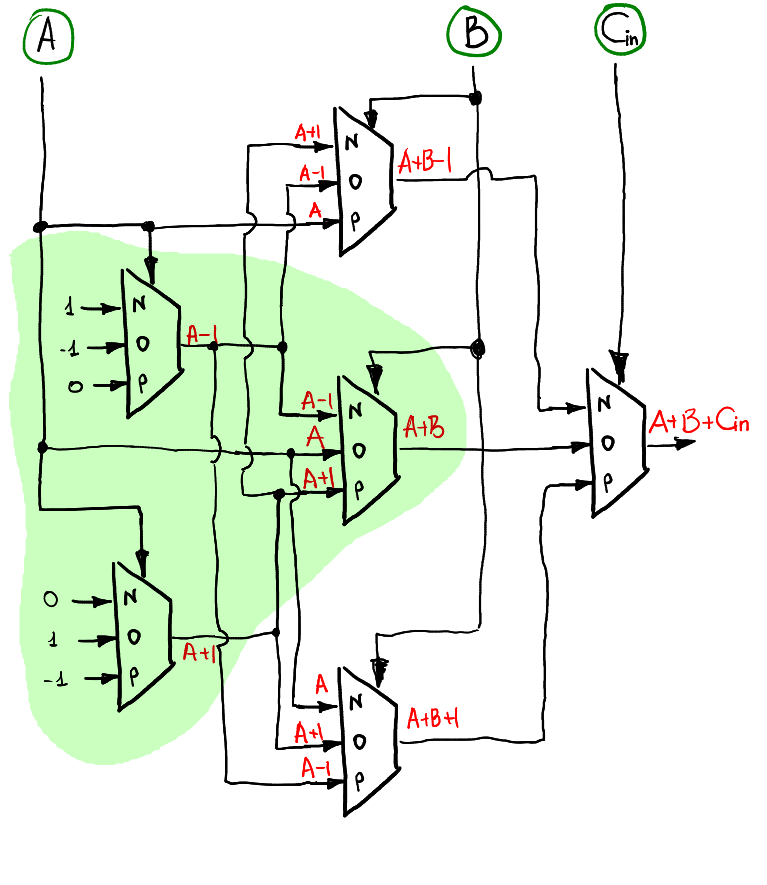
(圖五 全加器 Sum)

(圖六 全加器 Carry)
## Balanced Ternary 的設計要解決的問題類型
資料數值 $N_{10}$ 可以在 base 為 b 的計算系統中,使用 $\lfloor{log_bN + 1}\rfloor$ 個digits 來做表示,例如 $50_{10}$ 可以在 base 10 的計算系統中用 $\lfloor{log_{10}50 + 1}\rfloor=2$
The radix economy E(b,N) for any particular number N in a given base b is defined as $E(b,N)=b\lfloor{log_bN+1}\rfloor$
其中在 $b = e$ 時,radix economy 可以達到 minimal ,但是並沒有辦法做出 $digits = e$ 的處理器,而在 $b \in N$ 的情況下,minimal 在 $N=3$ 。
## 測試 Balanced Ternary
測試環境:Ubuntu 16.04.3 LTS
```
$ make check
echo 27 | ./b3k
├───┐
│ │
└───┘
echo -27 | ./b3k
┌┬──┐
│ │
└───┘
echo 9 | ./b3k
┌───┐
┤ │
└───┘
echo -9 | ./b3k
┌───┐
├ │
└───┘
```

## 想法 & 思考
經由測試結果,及參考圖猜測 - 往內 + 往外 0 則不變,四個邊四個腳分別為$3^0, 3^1, 3^2, 3^3, 3^4, 3^5, 3^6, 3^7$ 能表示的最大值為 $\sum\limits_{i=0}^{7}3^i=3280$ ,最小值為
$\sum\limits_{i=0}^{7}-3^i=-3280$。
此外依造圖上的計算模式可以來表示 balanced ternary 進位退位的運算
```
$ echo 1 | ./b3k
┌───┐
│ │
└─┬─┘
$ echo 0 | ./b3k
┌───┐
│ │
└───┘
$ echo -1 | ./b3k
┌───┐
│ │
└─┴─┘
$ echo 3281 | ./b3k
├─┴─┤
┤ ├
├─┬─┤
$ echo 3280 | ./b3k
├─┴─┤
┤ ├
├─┬─┤
$ echo 3279 | ./b3k
├─┴─┤
┤ ├
├───┤
$ echo -3279 | ./b3k
┌┬┬┬┐
├ ┤
└┴─┴┘
$ echo -3280 | ./b3k
┌┬┬┬┐
├ ┤
└┴┴┴┘
$ echo -3281 | ./b3k
┌┬┬┬┐
├ ┤
└┴┴┴┘
```
### 測試結果
經由程式結果知道,目前能表示的範圍為 $-3280$~$3280$
## 參考資料
[ 影片一 ](https://www.youtube.com/watch?v=vOyiHMa-mtQ)
[ 影片二 ](https://youtu.be/TFTK074nG_M)
[Ternary computing: basics](https://github.com/ssloy/tutorials/wiki/Ternary-computing:-basics)
[IOTA - isnt it the perfect Cryptocurrency?](https://www.reddit.com/r/CryptoCurrency/comments/6jgbvb/iota_isnt_it_the_perfect_cryptocurrency/dje8os2/)
[wikipedia Radix_economy](https://en.wikipedia.org/wiki/Radix_economy)
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet