---
tags: 資料結構,
---
# 資料結構 第一章 基本概念

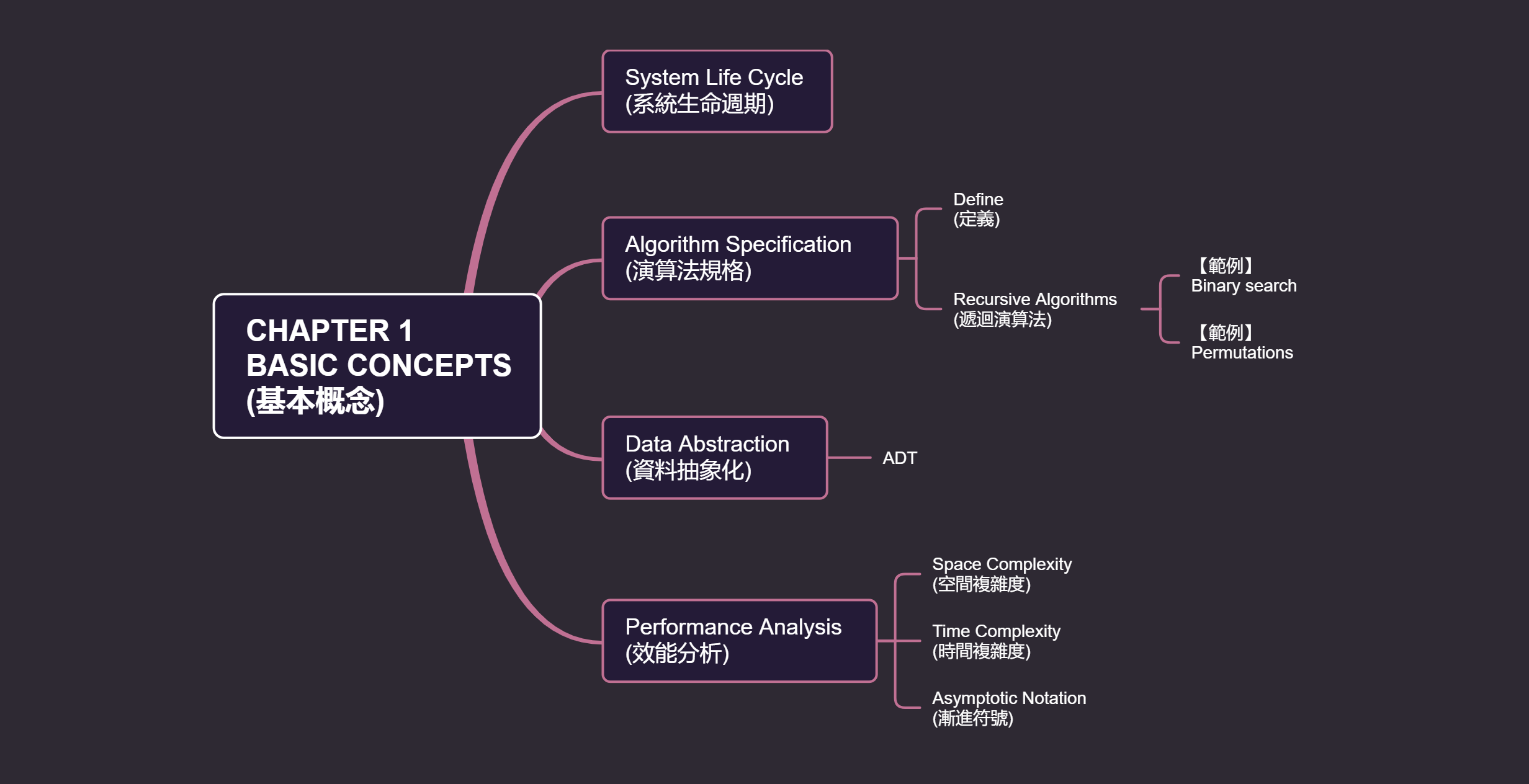
## 一、系統生命週期(System Life Cycle)
### (一)要求(Requirements)
制定所有情況下的輸入和輸出的描述
### (二)分析(Analysis)
#### 大致上分為兩種方式
(1) bottom-up：【由下至上EX：合併排序(Merge Sort)】
(2) top-down：【由下至上EX：快速排序(Quicksort Sort)】
### (三)設計(Design)
利用ADT來表示資料型態(EX：Array、List...etc)，與資料的操作(EX：插入、刪除...etc)
### (四)精細編碼(Refinement and coding)
在此階段實現ADT的操作。
### (五)驗證(Verification)
在此階段驗證程序(程式)的的正確性。

## 二、演算法(algorithm)
### (一)Definition 必須滿足下面五點
1.輸入(Input)：必須提供大於等於零的輸入
2.輸出(Output)：至少要產生一個輸出（不能沒有輸出）
3.確定性(Definiteness)：指令必須明確，不能模凌兩可。
4.有限性(Finiteness)：演算法必須在有限的步驟下結束。
5.有效性(Effectiveness)：原則上必須可以讓人使用鉛筆或紙追蹤此演算法。
### (二)遞迴演算法(Recursive Algorithms)
1.Define ：函數可以呼叫自己（self-calling）
2.遞迴類型
(1)直接遞迴(direct recursion)
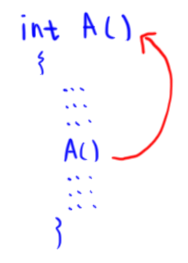
(2)間接遞迴(indirect recursion)

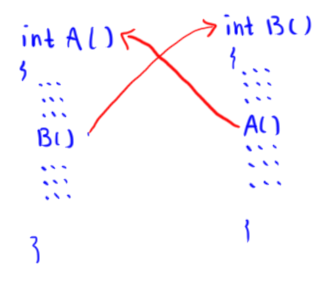
### (三)課本範例
1.【Binary search】:

int binsearch(int list[], int searchnum,int left, int right)
{
int middle;
if (left <= right)
{
middle =(left+right)/2;
switch(COMPARE(left[middle],searchnum))
{
case -1:
return binsearch(list,searchnum,middle+1,right);
case 0:
return middle;
case 1:
return binsearch(list,searchum,left,middle -1);
}
}
return -1;
}

---

想法概念操作如下：
Step1:計算出middle值
Step2:將middle值當作索引取出Array中的值
Step3:比較取出的值是否為搜尋的值
實際操作如下：

---

使用If else 【自己修改如有錯誤請賜教^^"】

int binsearch(int list[], int searchnum,int left, int right)
{
int middle;
if (left <= right)
{
middle =(left+right)/2;
if(left[middle]<searchnum)
return binsearch(list,searchnum,middle+1,right);
else if (left[middle]=searchnum)
return middle;
else // left[middle]>searchnum
return binsearch(list,searchum,left,middle -1);
}
return -1;
}

---

2.【Permutations】
void perm(char *list, int i ,int n)
{
int j, temp;
if(i==n)
{
for(j=0; j<=n ;j++)
print("%c",list[j]);
}
else
{
for(j=i; j <= n; j++)
{
swap(list[i],list[j],temp);
perm(list,i+1,n);
Swap(list[i],list[j],temp);
}
}
}

想法概念操作如下：
Step1:讓每個data輪流當排頭
Step2:進行排列組合

## 三、資料抽象化(Data Abstraction)
### (一)資料型態 (data type)
資料型態為物件的集合並包含對這些物件的操作及運算

### (二)抽象資料型態 (Abstract Data Type, ADT)
抽像數據型態（ADT）是這樣一種數據類型，其提供物件的操作等規範，其表示方法並非具體實現。

## 四、性能分析(Performance Analysis)

### (一)空間複雜度(Space Complexity)
#### 1.Definition：
隨著資料量的增加程序完成運行所需記憶體空間的成長
#### 2.空間類型區分兩種
1.固定空間(Fixed space)
2.變動空間(Variable space)

### (二)時間複雜度(Time Complexity)
#### Definition：
程序完成執行所需的計算機時間
### (三)漸進符號(Asymptotic Notation)
#### 1.Definition　Ｏ[Big “oh”]
f(n)= O(g(n)) iff there exist positive constants c and n~0~ such that f(n) < cg(n) for all n, n > n~0~

#### Definition: Ω[Omega]
f(n)= Ω(g(n)) iff there exist positive constants c and n~0~ such that f(n) > cg(n) for all n, n > n~0~

#### Definition: Θ[Theta]
f(n)= Θ(g(n)) iff there exist positive constants c~1~, c~2~, and n0 such that c~1~g(n) < f(n) < c~2~g(n) for all n, n > n~0~

### (四)實踐複雜性(Practical Complexities)


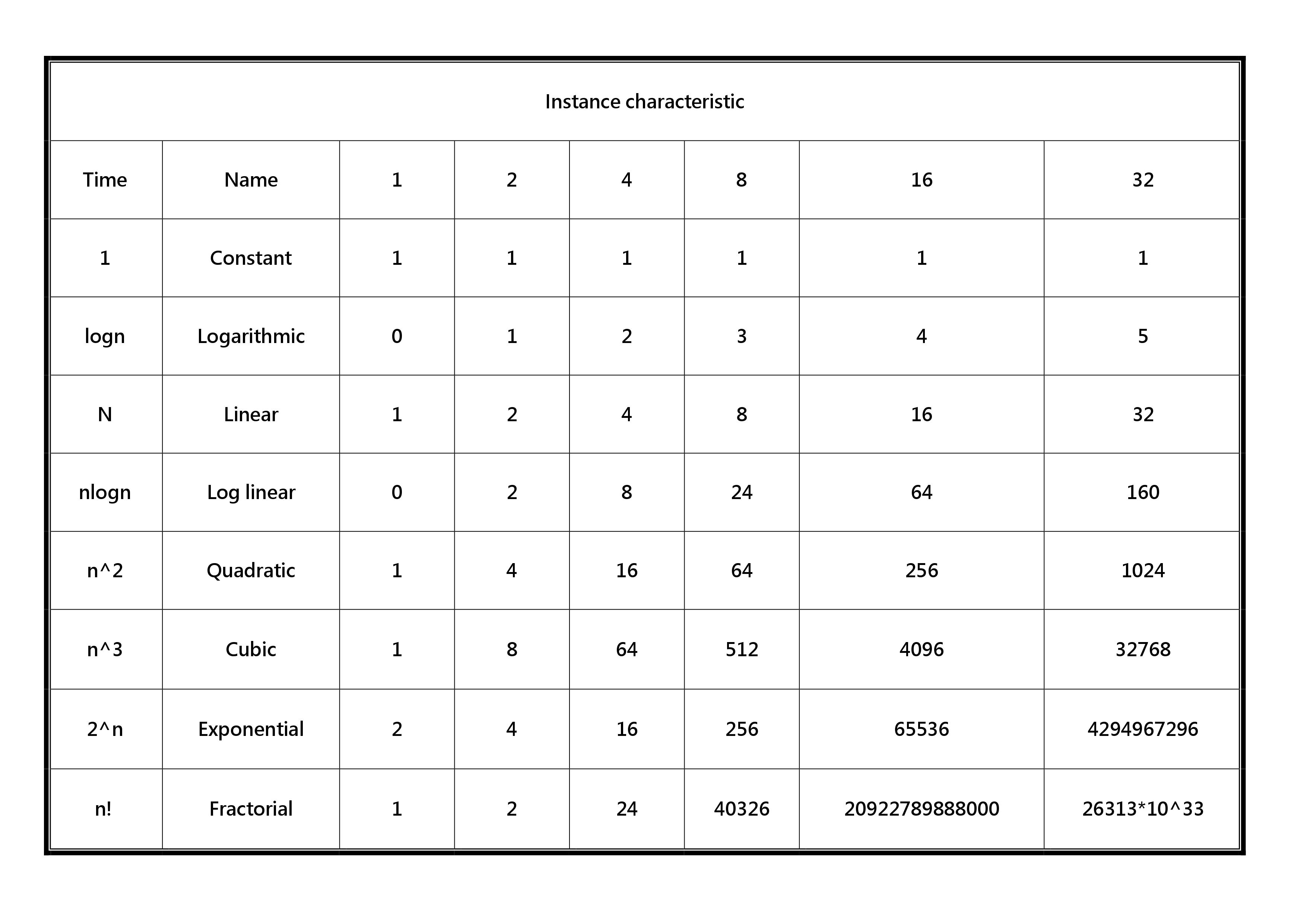
## 五、效能評估(Performance Measurement)


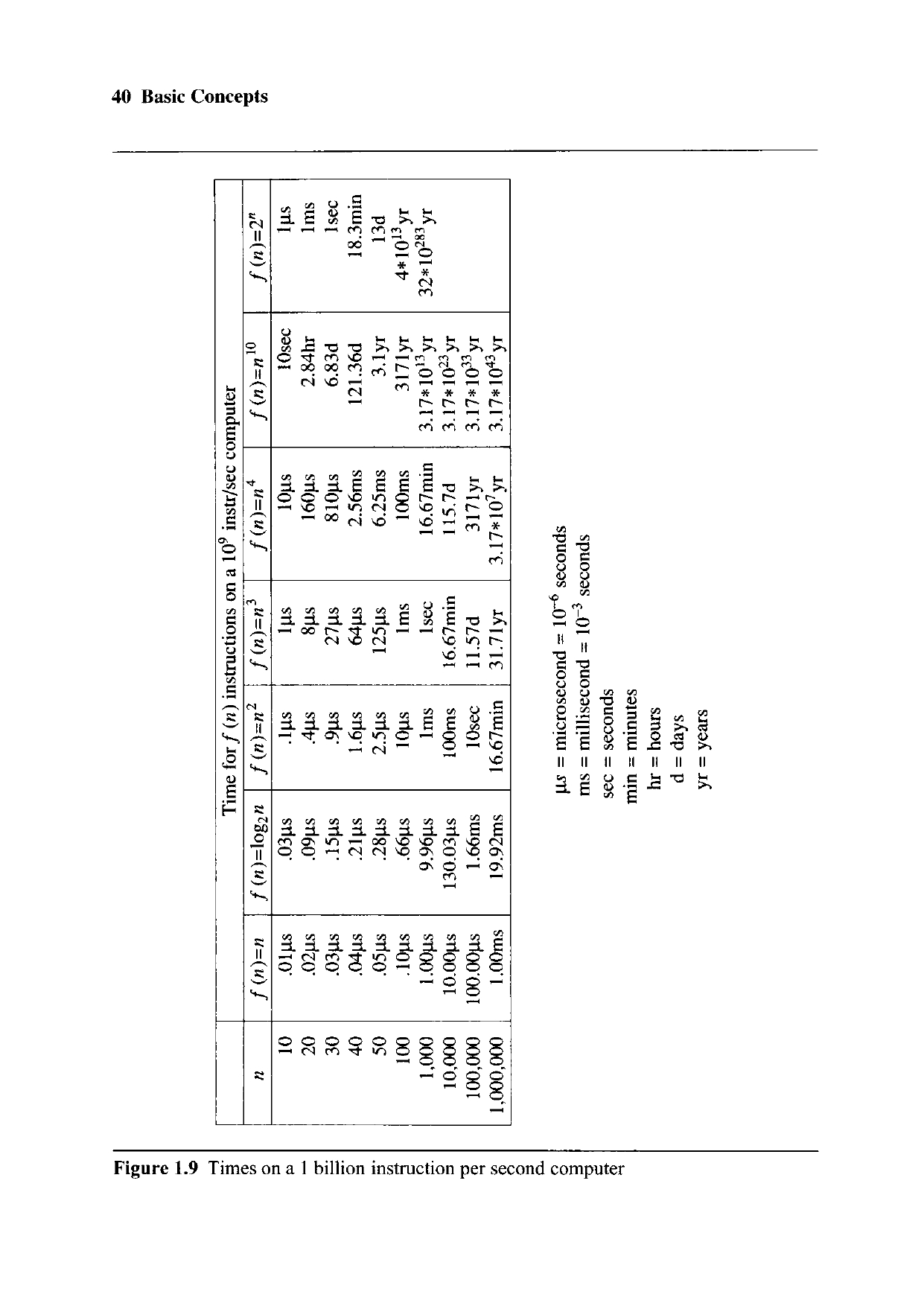
> 參考資料:Fundamentals of Data Structures in C by Ellis Horowitz, Sartaj Sahni, Susan Anderson-Freed