# TP MATALB

# Génération d'un signal aléatoire

clc; % Efface la fenêtre de commande 
clearvars; % Efface toutes les variables de l'espace de travail 
close all; % Ferme toutes les fenêtres de figure ouvertes

% Différents nombres de points
nb_points = [128, 256, 512, 1024];

% Préparation de la figure pour afficher les DSP
figure;

for i = 1:length(nb_points)

    % Définition des paramètres
    fe = 1; % Fréquence d'échantillonnage en Hz

    % Génération du bruit gaussien pour le nombre de points actuel
    t = (0:nb_points(i)-1) * (1/fe); % Vecteur temps
    bruit = randn(1, nb_points(i)); % Génération du bruit gaussien

    % Affichage du signal dans le domaine temporel
    subplot(length(nb_points), 2, 2*i-1);
    plot(t, bruit);
    xlabel('Temps (s)');
    ylabel('Amplitude');
    title(['Signal de bruit gaussien - ', num2str(nb_points(i)), ' points']);

    % Calcul de la transformée de Fourier discrète (TFD)
    TFD = fft(bruit);

    % Centre la TFD dans la plage de fréquences [-1/2 ; 1/2]
    TFD_centree = fftshift(TFD);

    % Calcul de la DSP
    DSP = (1/nb_points(i)) * abs(TFD_centree).^2;
    moy = mean(DSP);

    % Création du vecteur fréquence centré
    freq = (-nb_points(i)/2:nb_points(i)/2-1) * (fe/nb_points(i));
    
    % Plot de la DSP centrée en 0
    subplot(length(nb_points), 2, 2*i);
    plot(freq, DSP,'r',freq, moy*ones(size(freq)),'b');
    xlabel('Fréquence (Hz)');
    ylabel('DSP');
    title(['DSP pour ', num2str(nb_points(i)), ' points']);
end


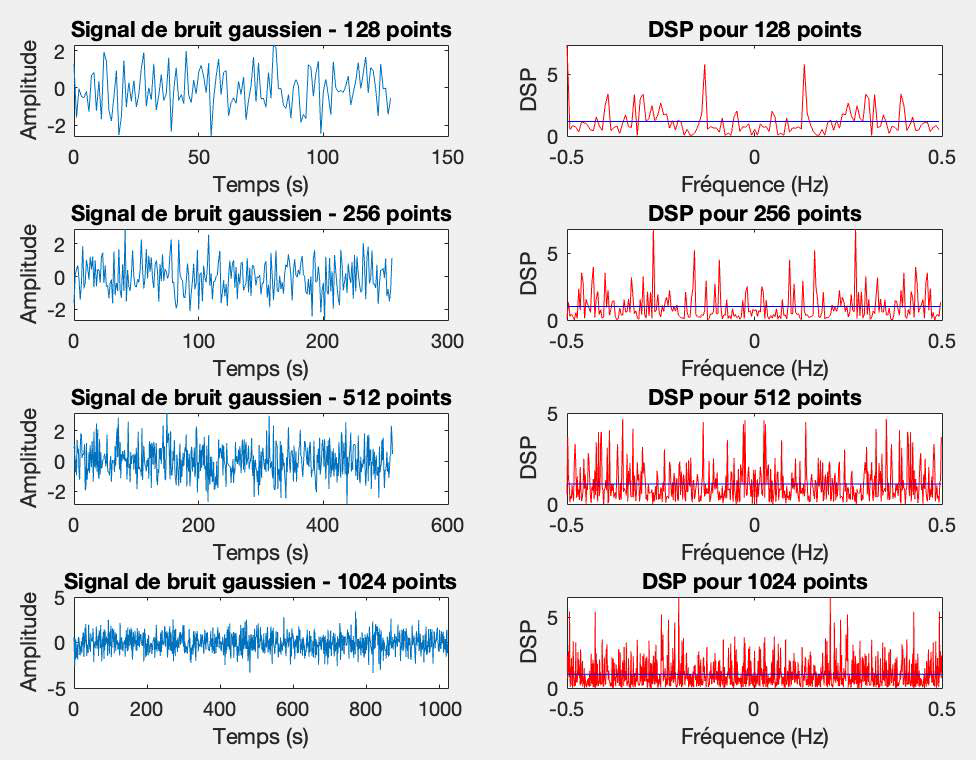
On constate une valeur moyenne constante, bien que des perturbations persistent probablement dues à une variance non nulle. L'augmentation du nombre de points offre une visibilité plus claire de la valeur moyenne, cependant, cela n'affecte pas la présence des variations.

## Calculer l’espérance mathématique et la variance de M.

$M=\frac{m(1)+m(2)}{2}=\frac{(Q+e(1))+(Q+e(2))}{2}=Q+\frac{e(1)+e(2)}{2}$

$$
\mathbb{E}(M)=\mathbb{E}\left(Q+\frac{e(1)+e(2)}{2}\right)
$$

Comme $\mathbb{E}(e(1))=\mathbb{E}(e(2))=0$ (erreur de moyenne nulle):
$$
\mathbb{E}(M)=\mathbb{E}(Q)+\frac{\mathbb{E}(e(1)+e(2))}{2}=Q
$$

$$
\operatorname{Var}(M)=\operatorname{Var}\left(Q+\frac{e(1)+e(2)}{2}\right)
$$

Comme $e(1)$ et $e(2)$ sont indépendants:
$$
\begin{aligned}
& \operatorname{Var}(M)=\operatorname{Var}\left(Q+\frac{e(1)}{2}+\frac{e(2)}{2}\right) \\
& \operatorname{Var}(M)=\operatorname{Var}(Q)+\frac{1}{4} \operatorname{Var}(e(1))+\frac{1}{4} \operatorname{Var}(e(2)) \\
& \text { Comme } \operatorname{Var}(e(1))=\operatorname{Var}(e(2))=\sigma^2: \\
& \operatorname{Var}(M)=\operatorname{Var}(Q)+\frac{\sigma^2}{2}
\end{aligned}
$$

Donc, la variance de $M$ est $\operatorname{Var}(Q)+\frac{\sigma^2}{2}$. Notez que si $Q$ est une quantité constante, alors $\operatorname{Var}(Q)=0$ et la variance de $M$ est simplement $\frac{\sigma^2}{2}$.

## Comment évolue la variance de la mesure ?

Si $Q$ est une quantité constante, la variance de la mesure $M$ est principalement influencée par la variance des erreurs de mesure $\left(\sigma^2\right)$.

Si les erreurs de mesure sont faibles, la variance de $M$ sera également faible, ce qui indique une mesure plus précise. En revanche, si les erreurs de mesure sont élevées, la variance de $M$ sera également élevée, ce qui indique une mesure moins précise. La constance de $Q$ n'affecte pas directement la variance de $M$, sauf si elle est associée à des erreurs de mesure.

## Proposer alors une méthode pour améliorer le calcul des DSP des signaux aléatoires.

AVOIRE EN FONCTION DES RESUSTATS

Le calcul des densités spectrales de puissance (DSP) des signaux aléatoires peut être amélioré en utilisant des techniques appropriées de moyennage et de réduction du bruit. Voici quelques méthodes couramment utilisées pour améliorer le calcul des DSP des signaux aléatoires :

1. **Moyennage Temporel**:
- Acquérir plusieurs échantillons du signal aléatoire.
- Calculer la DSP pour chaque échantillon individuel.
- Moyenner les DSP pour obtenir une DSP moyenne.
- Le moyennage permet de réduire les fluctuations aléatoires et d'améliorer la précision de la DSP.

2. **Moyennage Fréquentiel**:
- Diviser le signal en segments plus petits.
- Calculer la DSP pour chaque segment.
- Moyenner les DSP des segments pour obtenir une DSP moyenne.
- Utile lorsque la DSP varie dans le temps.

3. **Fenêtrage**:
- Appliquer une fenêtre à chaque segment de signal avant de calculer la transformée de Fourier.
- Cela réduit les effets de fuite spectrale.
- Des fenêtres telles que la fenêtre de Hamming ou la fenêtre de Blackman-Harris sont couramment utilisées.

4. **Moyennage Croisé**:
- Utiliser le moyennage croisé pour estimer la DSP croisée entre deux signaux.
- Utile pour l'analyse de signaux aléatoires multivariés.

5. **Utilisation de Périodes plus Longues**:
- Si le signal aléatoire présente une structure sur une période plus longue, augmenter la longueur de l'échantillon pour capturer cette structure.

6. **Méthodes de Réduction du Bruit**:
- Utiliser des techniques de réduction du bruit telles que le filtrage numérique pour minimiser les effets du bruit sur la DSP.

7. **Utilisation de Modèles Probabilistes**:
- Si des modèles probabilistes sont disponibles pour le signal, les incorporer dans le calcul de la DSP pour une estimation plus précise.

8. **Utilisation de Méthodes Avancées**:
- Pour des applications spécifiques, des méthodes avancées telles que la transformée en ondelettes peuvent être utilisées pour mieux représenter le contenu fréquentiel du signal.

# UNE EXPÉRIENCE VS PLUSIEURS EXPÉRIENCES

% Paramètres de base
fe = 1; % Fréquence d'échantillonnage en Hz
N = 128; % Nombre de points
n_samples = [5, 20, 100, 500]; % Nombre de tirages pour chaque groupe

% Préparation des graphiques
figure;

for idx = 1:length(n_samples)
    % Calculer la moyenne des DSP pour chaque nombre de tirages
    mean_dsp = zeros(1, N);
    for i = 1:n_samples(idx)
        % Générer un tirage de bruit
        noise = randn(1, N);
        
        % Calculer la FFT et la DSP
        fft_result = fft(noise);
        dsp = abs(fft_result).^2 / N;
        mean_dsp = mean_dsp + dsp;
    end
    mean_dsp = mean_dsp / n_samples(idx);
    
    % Fréquences correspondantes, limitées à l'intervalle [-fe/2, fe/2]
    freq = (-N/2:N/2-1)*(fe/N);
    mean_dsp = fftshift(mean_dsp); % Centrer la DSP autour de zéro

    % Tracer la DSP moyenne
    subplot(2, 2, idx);
    plot(freq, mean_dsp);
    title(['Moyenne DSP pour ', num2str(n_samples(idx)), ' tirages']);
    xlabel('Fréquence (Hz)');
    ylabel('DSP');
    grid on;
end


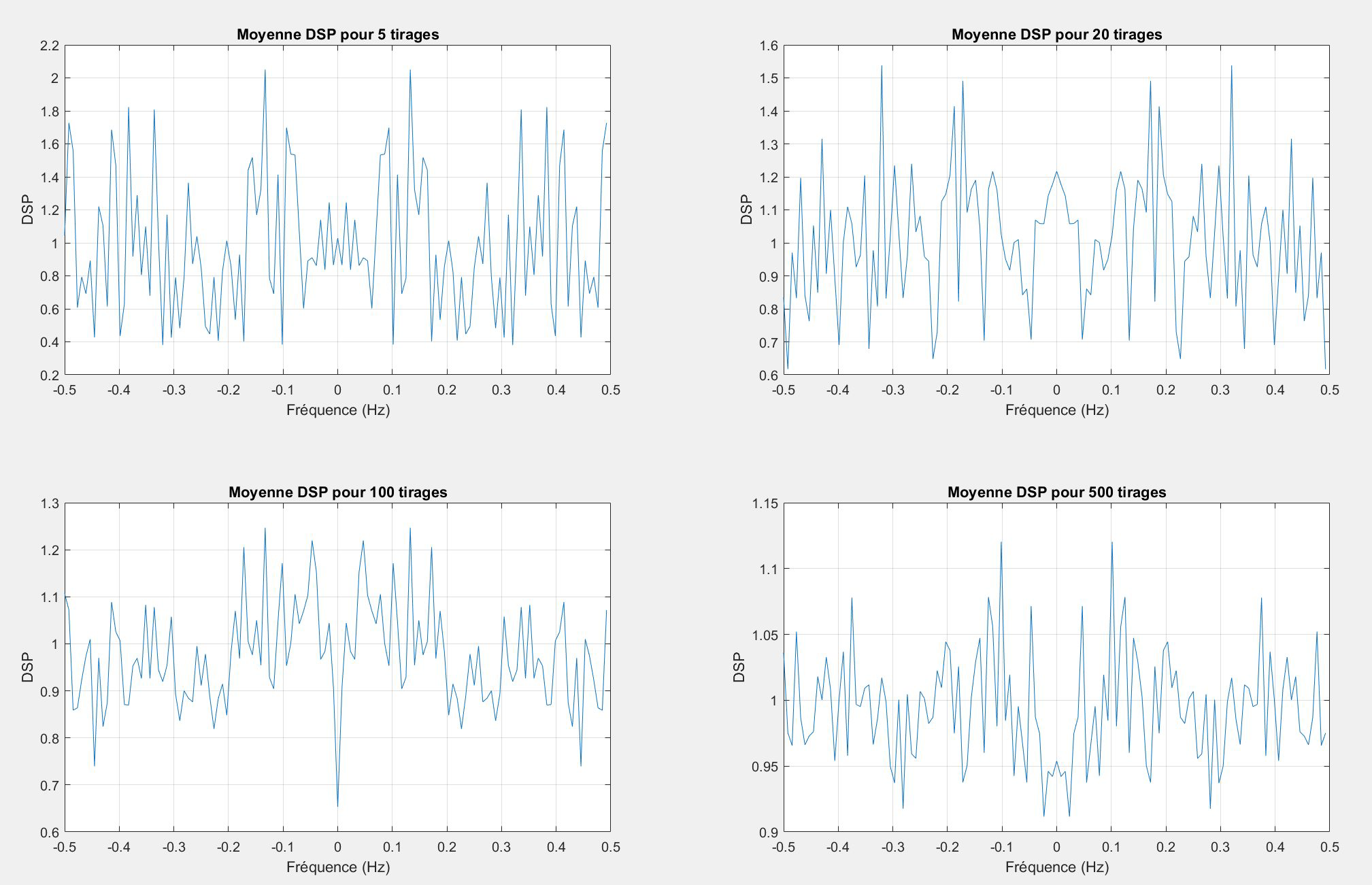
En analysant de petits groupes d'échantillons (5 ou 20) en DSP, on remarque de grandes variations, ce qui est normal à cause de leur petite taille. Quand on augmente le nombre d'échantillons (100, 500), les résultats deviennent plus uniformes, ce qui suit la logique des statistiques. Cependant, les résultats ne sont jamais complètement réguliers, mais tendent à se stabiliser autour d'une valeur moyenne, un phénomène courant avec le bruit blanc où toutes les fréquences se mélangent de manière égale.

# Etude d'un signal bruité

Si l'expérience est divisée en M sous-ensembles équitablement, la durée temporelle de chaque sous-expérience sera proportionnelle à l'inverse du nombre de sous-ensembles $\frac{T}{M}$. Si la division est basée sur des critères temporels spécifiques, la durée de chaque sous-expérience dépendra de ces critères et peut varier en fonction de la nature du signal mesuré.

Densité spectrale de puissance théorique du signal connu pour tout $t$

Pour calculer la densité spectrale de puissance théorique, on commence par l'autocorrélation :
$$
R_s(\tau)=E[\cos (2 \pi 20 t)+\cos (2 \pi 20.1 t)+b(t)][\cos (2 \pi 20(t-\tau))+ cos (2 \pi 20.1(t-\tau))+b(t-\tau)]
$$
Ensuite nous faisons la transformée de Fourier de l'autocorrélation :
$$
S(f)=\mathcal{F}\left\{R_s(\tau)\right\}
$$
On utilise, pour les composantes sinusoïdales, la propriété :
$$\mathcal{F}\left\{\cos \left(2 \pi f_0 t\right)\right\}=\frac{1}{2}\left(\delta\left(f-f_0\right)+\delta\left(f+f_0\right)\right)$$
Donc pour $f=20 \mathrm{~Hz}$ et $f=20.1 \mathrm{~Hz}$ :
$$
S(20) \text { et } S(20.1)
$$

Théoriquement nous trouvons un spectre avec deux pics en $f=20 \mathrm{~Hz}$ et $f=20.1 \mathrm{~Hz}$ avec du bruit constant.

Voici ce que cela pourrais représenter :


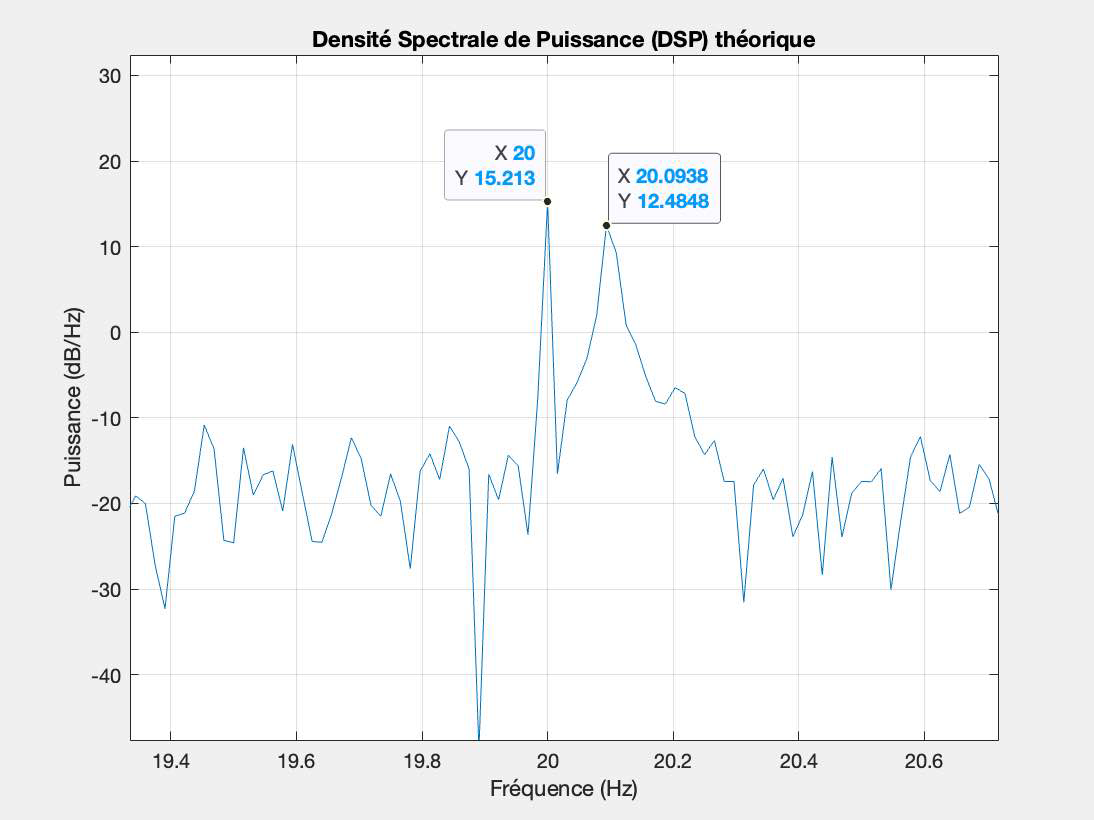
Voici le code qui à permis de l'obtenir :

clc; % Efface la fenêtre de commande

clearvars; % Efface toutes les variables de l'espace de travail

close all; % Ferme toutes les fenêtres de figure ouvertes

fe = 128; % Fréquence d'échantillonnage en Hz

t = 0:1/fe:(8192-1)/fe; % Vecteur temporel

% Signal s(t)

s = cos(2*pi*20*t) + cos(2*pi*20.1*t) + randn(size(t)); % Ajout du bruit gaussien

N = length(s);

xdft = fft(s);

xdft = xdft(1:N/2+1);

psdx = (1/(fe*N)) * abs(xdft).^2;

psdx(2:end-1) = 2*psdx(2:end-1);

freq = 0:fe/length(s):fe/2;

% Affichage de la DSP

figure;

plot(freq, 10*log10(psdx));

title('Densité Spectrale de Puissance (DSP) théorique');

xlabel('Fréquence (Hz)');

ylabel('Puissance (dB/Hz)');

grid on;

Désormais on calcule et représente la DSP calculée à partir des 8192 points de mesure en considérant :
- 1 sous-expérience de 8192 points,
- 2 sous-expériences de 4096 points,
- 4 sous-expériences de 2048 points,
- 8 sous-expériences de 1024 points,
- 16 sous-expériences de 512 points,
- 32 sous-expériences de 256 points.

clc; % Efface la fenêtre de commande

clearvars; % Efface toutes les variables de l'espace de travail

close all; % Ferme toutes les fenêtres de figure ouvertes

fe = 128; % Fréquence d'échantillonnage en Hz

t = 0:1/fe:(8192-1)/fe; % Vecteur temporel

% Signal s(t)

s = cos(2*pi*20*t) + cos(2*pi*20.1*t) + randn(size(t)); % Ajout du bruit gaussien

% Tailles des sous-expériences

subexp_sizes = [8192, 4096, 2048, 1024, 512, 256];

% Représentation graphique

figure;

for i = 1:length(subexp_sizes)

N_subexp = subexp_sizes(i);

[psd, freq] = pwelch(s, rectwin(N_subexp), 0, N_subexp, fe);

subplot(length(subexp_sizes), 1, i);

plot(freq, 10*log10(psd));

title(['DSP avec ', num2str(N_subexp), ' points']);

xlabel('Fréquence (Hz)');

ylabel('Puissance (dB/Hz)');

grid on;

end


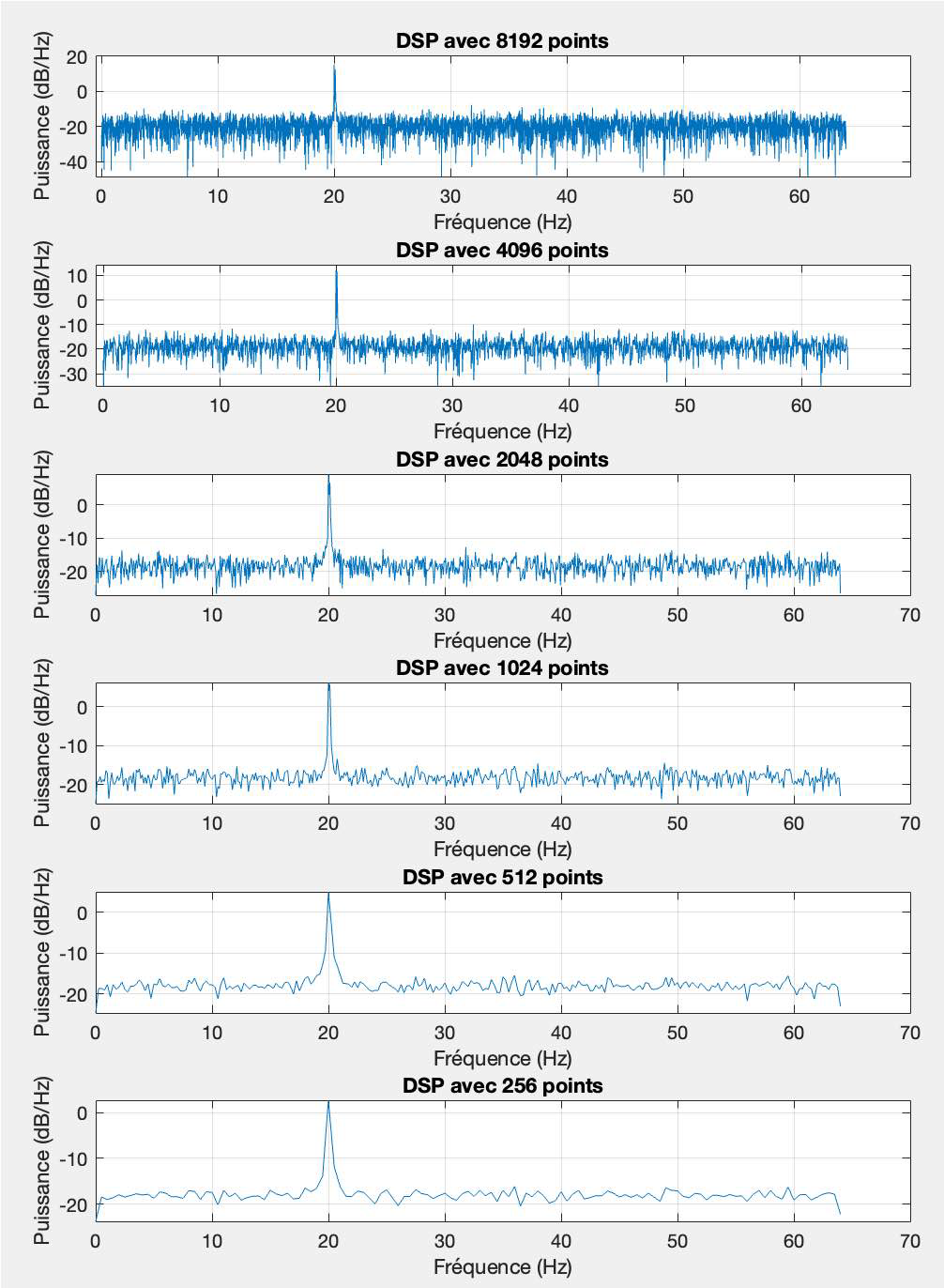
En observant l'évolution des différentes DSP calculées pour des tailles de sous-expériences croissantes, on voit un compromis entre la résolution fréquentielle et la réduction du bruit. Des DSP avec plus de points offrent une meilleure résolution, mais elles peuvent être plus sensibles au bruit.

L'estimation spectrale est souvent réalisée en moyennant plusieurs réalisations du signal ou en utilisant des fenêtres pour diviser le signal en segments.

- Biais : Il s'agit de l'erreur systématique introduite par le processus d'estimation. Une méthode de moyennage peut introduire un biais en lissant le spectre, en particulier aux fréquences où le signal change rapidement.

- Variance : C'est la dispersion des estimations autour de la vraie valeur. Une méthode de moyennage peut réduire la variance en atténuant le bruit, mais cela peut également entraîner une perte de résolution.

Ainsi, le compromis biais-variance suggère qu'il existe un équilibre délicat entre la réduction du bruit et la préservation de la résolution lors de l'estimation spectrale par moyennage.