# Exercice 1 :


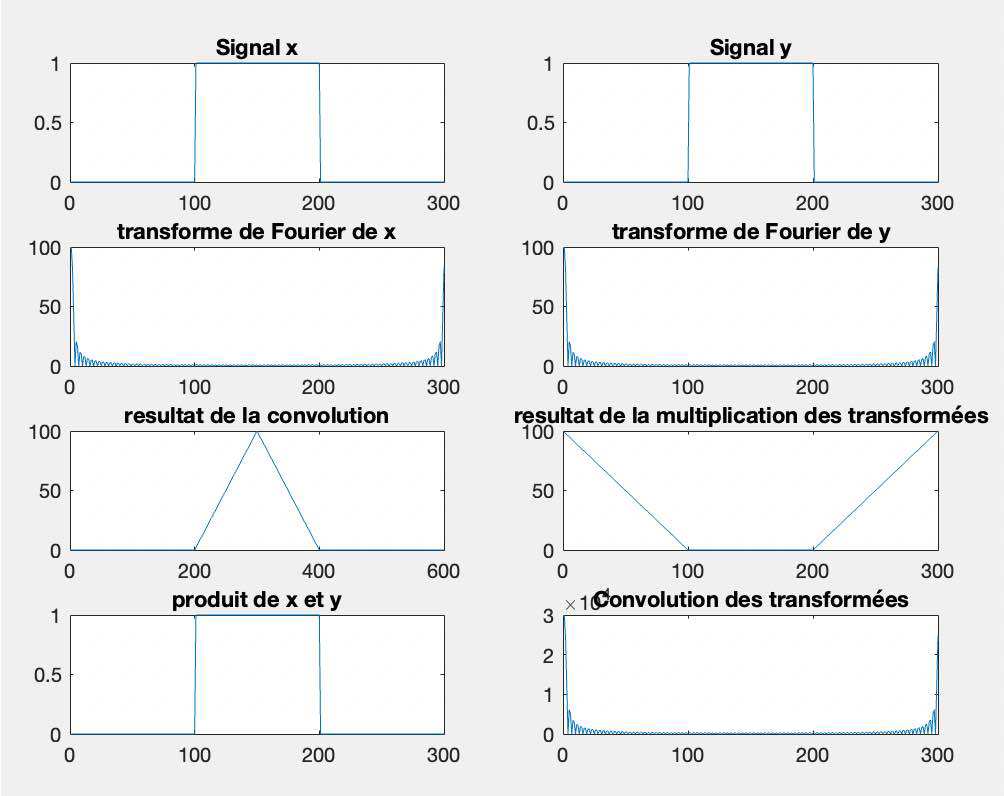
La convolution de \( x \) et \( y \) donne le résultat attendu. La forme triangulaire obtenue est caractéristique de la convolution de deux fonctions porte. La multiplication des transformées de Fourier \( X \) et \( Y \) suivie d'une transformée de Fourier inverse produit également une forme triangulaire. Ceci est cohérent avec le théorème de Plancherel. La multiplication des signaux \( x \) et \( y \) donne une fonction porte, car les deux signaux sont identiques. Cependant, pour la convolution des transformées de Fourier \( X \) et \( Y \) suivie d'une transformée de Fourier inverse, la convolution des transformées de Fourier et la transformée de Fourier inverse donnent une fonction qui représente la multiplication des signaux \( x \) et \( y \) dans le domaine temporel, ce qui confirme la deuxième partie du théorème de Plancherel.

# Exercice 2 :

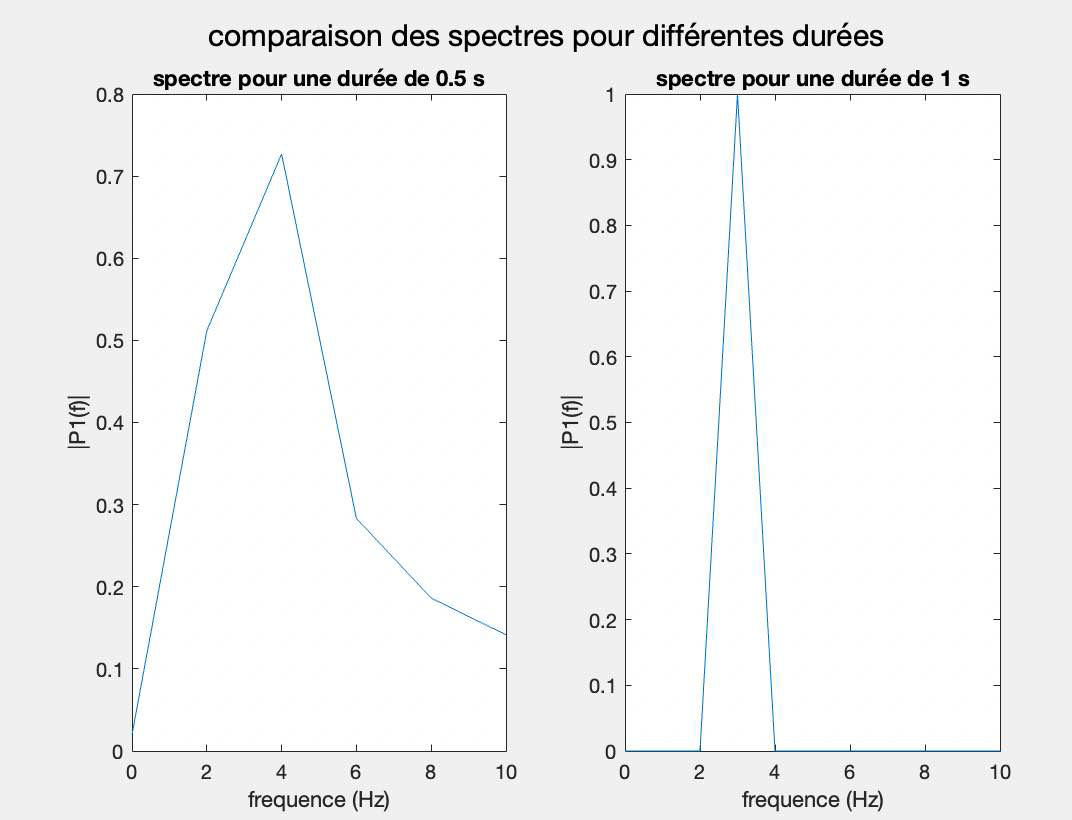
Lorsque la durée du signal passe de 0,5 seconde à 1 seconde, le pic spectral devient plus étroit et plus défini. Cela est dû à une meilleure résolution dans le domaine fréquentiel.En, effet une fenêtre temporelle plus longue permet une détection plus précise des composants fréquentiels.

# Exercice 3 :

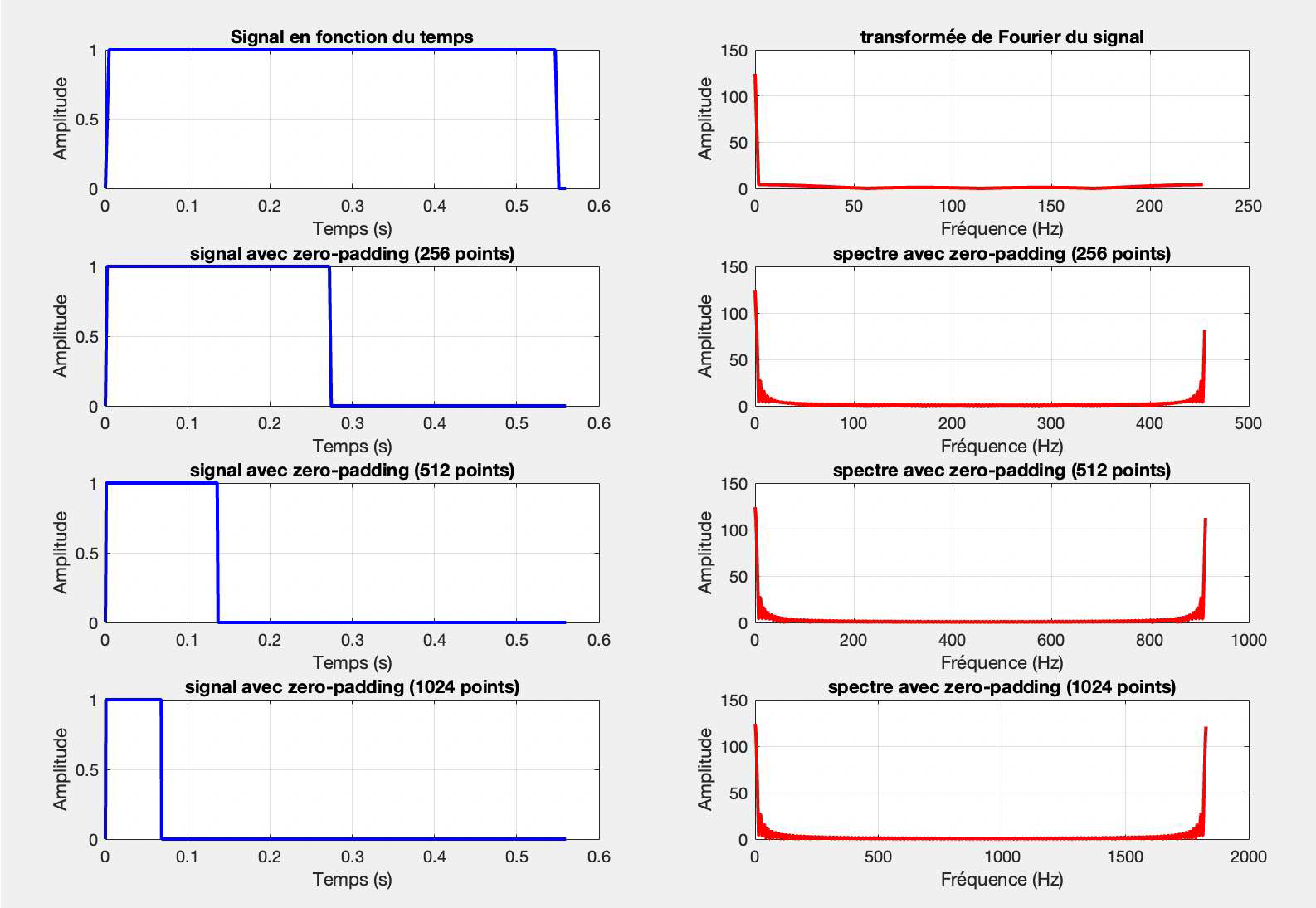
Le premier graphique représente un signal rectangulaire dans le domaine temporel, avec une amplitude de 1. Le graphique à droite montre la transformée de Fourier de ce signal, mettant en évidence un pic principal et des lobes latéraux, caractéristiques d'un signal rectangulaire.

Les graphiques suivants présentent l'effet du zero-padding. Avec 256 points de zero-padding, la résolution en fréquence s'améliore, permettant une distinction plus nette des composantes fréquentielles. Avec 512 points de zero-padding, le spectre devient encore plus détaillé. Enfin, avec 1024 points de zero-padding, la résolution de fréquence est très précise, offrant une visualisation détaillée des composantes fréquentielles du signal. Dans tous les cas, la forme temporelle du signal reste inchangée, mais l'échelle temporelle est étendue pour inclure plus de points.

# Exercice 4:

# Exercice 5


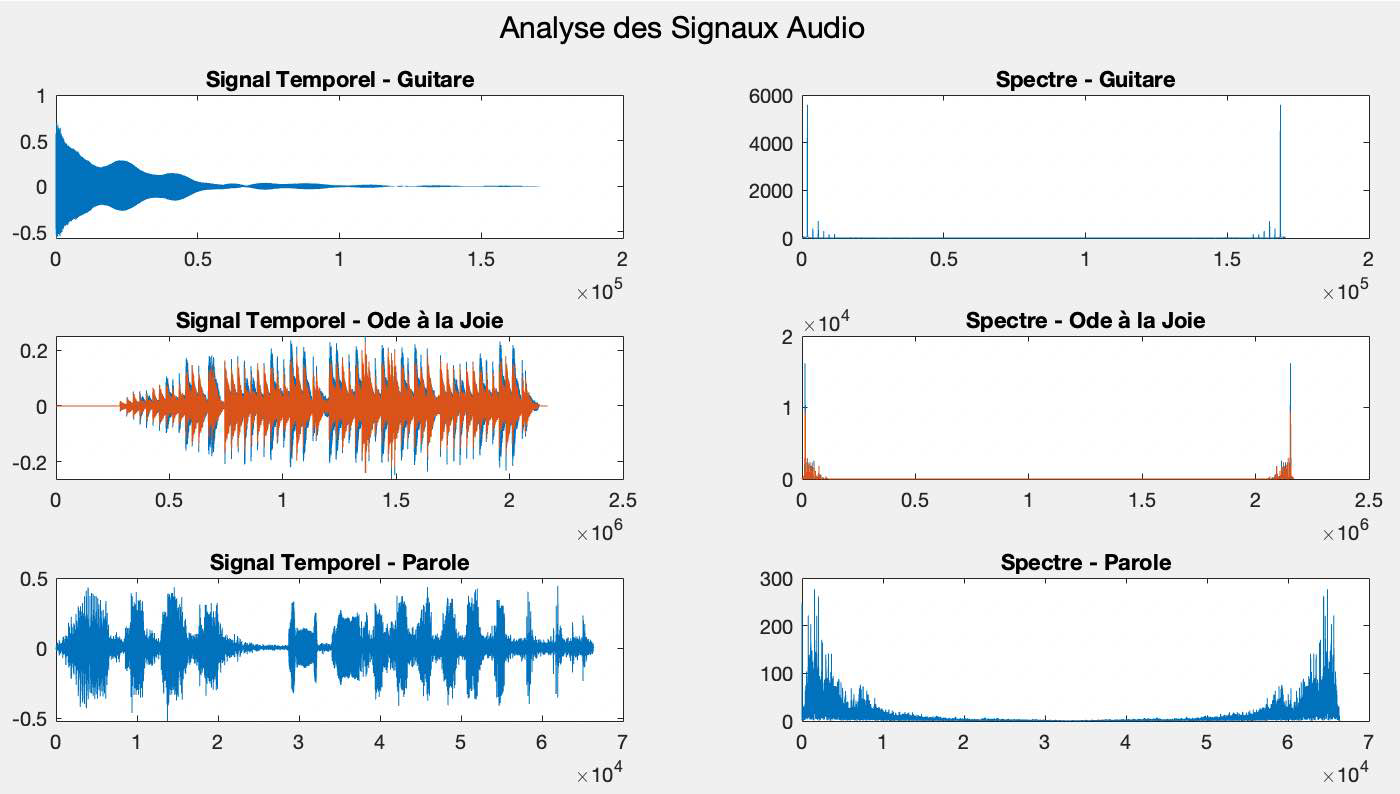
**a- La guitare**

La fréquence fondamentale du fichier guitar.wav est d'environ 486.33 Hz. Ce qui corresponds à la note Si (B4).
​
**b- L’hymne à la joie au piano**

Le spectre fournit des détails sur les composantes fréquentielles du son, tandis que la vue temporelle montre la dynamique et le rythme du morceau.

**c- La parole**