# Visualisation de la compression JPEG

1. Examinez la taille des fichiers créés. Jusqu’à quel taux de compression jugez-vous que la dégradation n’est pas visible?

clc; % Efface la fenêtre de commande
clearvars; % Efface toutes les variables de l'espace de travail
close all; % Ferme toutes les fenêtres de figure ouvertes

im = imread('lena.bmp');

% Crée une nouvelle figure avec deux sous-fenêtres (1 ligne, 2 colonnes)
figure;

% Première sous-fenêtre
subplot(1, 2, 1);
imagesc(im);
colormap gray;
title('Image originale');

% Enregistre l'image avec une qualité réduite
imwrite(im, 'lena.jpg', 'quality', 5);

% Lit l'image enregistrée
im = imread('lena.jpg');

% Deuxième sous-fenêtre
subplot(1, 2, 2);
imagesc(im);
colormap gray;
title('Image avec qualité réduite à 5');

Il apparaît clairement, lorsqu'on examine le contenu avec un facteur de qualité de 100, que l'image n'a subi aucune altération apparente. Cependant, le fichier .jpg associé affiche une taille de 219 Ko, en comparaison des 769 Ko de l'image d'origine. Une observation attentive révèle une légère altération lorsque le facteur de qualité est réduit à 50, et la taille de l'image est alors réduite à seulement 25 Ko. À un niveau de qualité de 25, l'altération visuelle devient manifeste, et la taille de l'image diminue considérablement à 16 Ko. À un facteur de qualité de 10, l'image devient nettement floue, tandis qu'à 5, d'énormes pixels sont discernables. À 0, les couleurs de l'image subissent une transformation significative, et il devient difficile de reconnaître même la silhouette de Lena.


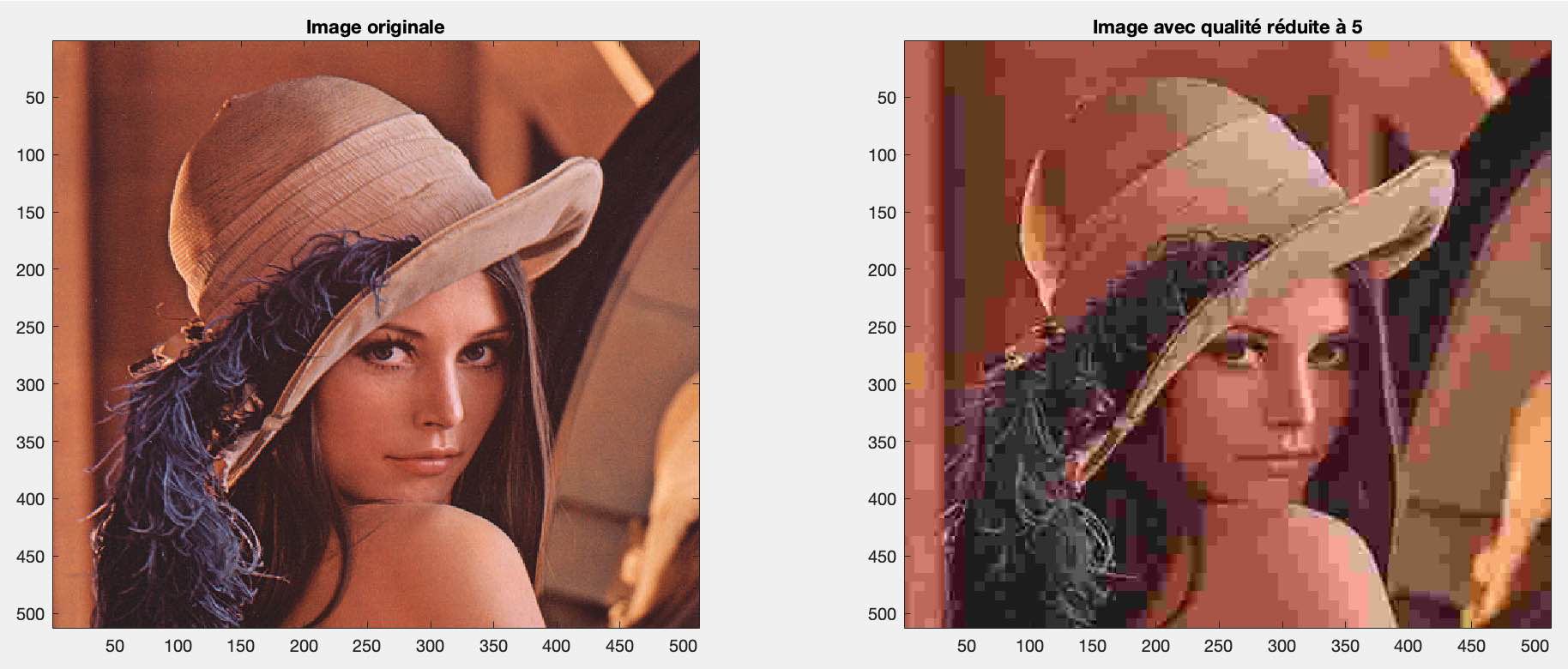
2. Sur quelles zones de l’image commencez-vous à observer des dégradations? Au contraire, quelles sont les zones qui supportent les plus gros taux de compression?

Il semble que la compression soit mieux tolérée par les couleurs sombres. En effet, les cheveux de Lena montrent peu de modifications, alors que sur son épaule et son visage, les pixels deviennent nettement plus visibles.

# Compression

La fonction `fft` en MATLAB renvoie la transformée de Fourier discrète (DFT) d'un signal, mais elle renvoie les fréquences dans l'intervalle [0, fe], où fe est la fréquence d'échantillonnage. Dans le contexte de traitement d'images, cela signifie que les fréquences basses (basses fréquences spatiales) sont situées près du centre de l'image dans la représentation de la transformée de Fourier.

Les hautes fréquences sont situées dans les coins de l'image dans la représentation de la transformée de Fourier. La fonction `fftshift` est utilisée pour déplacer ces hautes fréquences du coin vers le centre, et vice versa.

Pour créer un filtre qui extrait les hautes fréquences, il faut définir une zone circulaire centrée dans l'image (dans le domaine de Fourier) et la remplir de zéros, laissant le reste de l'image inchangé.

% Lire l'image
lena = imread('lena.bmp');

% Déterminer le type de l'image
if size(lena, 3) == 1
	disp('L''image est en niveaux de gris.');
elseif size(lena, 3) == 3
	disp('L''image est en couleur.');
end

% Convertir l'image en niveaux de gris si ce n'est pas déjà le cas
if size(lena, 3) == 3
	lena = rgb2gray(lena);
end

% Calculer la transformée de Fourier 2D
lena_fft = fft2(double(lena));

% Centrer la transformée de Fourier
lena_fft_shifted = fftshift(lena_fft);

% Afficher l'image originale
subplot(1, 2, 1);
imshow(lena);
title('Image originale');

% Afficher la magnitude de la transformée de Fourier
subplot(1, 2, 2);
imshow(log(1 + abs(lena_fft_shifted)), []);
title('Transformée de Fourier');

% Ajouter des titres et des légendes
sgtitle('Transformée de Fourier de lena.bmp');

% Afficher les axes
axis on;

% Calculer la transformée de Fourier 2D
lena_fft = fft2(double(lena));

% Centrer la transformée de Fourier
lena_fft_shifted = fftshift(lena_fft);

% Afficher l'image originale et la transformée de Fourier centrée
subplot(1, 3, 1);
imshow(lena);
title('Image originale');
subplot(1, 3, 2);
imshow(log(1 + abs(lena_fft)), []);
title('Transformée de Fourier (non centrée)');
subplot(1, 3, 3);
imshow(log(1 + abs(lena_fft_shifted)), []);
title('Transformée de Fourier (centrée)');

% Créer un filtre pour extraire les hautes fréquences
[m, n] = size(lena);
radius = 30; % rayon de la zone circulaire
center = [m/2, n/2]; % centre de l'image
[x, y] = meshgrid(1:n, 1:m);
high_pass_filter = double(((x - center(2)).^2 + (y - center(1)).^2) > radius^2);

% Appliquer le filtre dans le domaine de Fourier
lena_fft_high_pass = lena_fft_shifted .* high_pass_filter;

% Effectuer la transformée de Fourier inverse
lena_high_pass = ifft2(ifftshift(lena_fft_high_pass));

% Afficher l'image obtenue après extraction des hautes fréquences
figure;
imshow(abs(lena_high_pass), []);
title('Image obtenue après extraction des hautes fréquences');



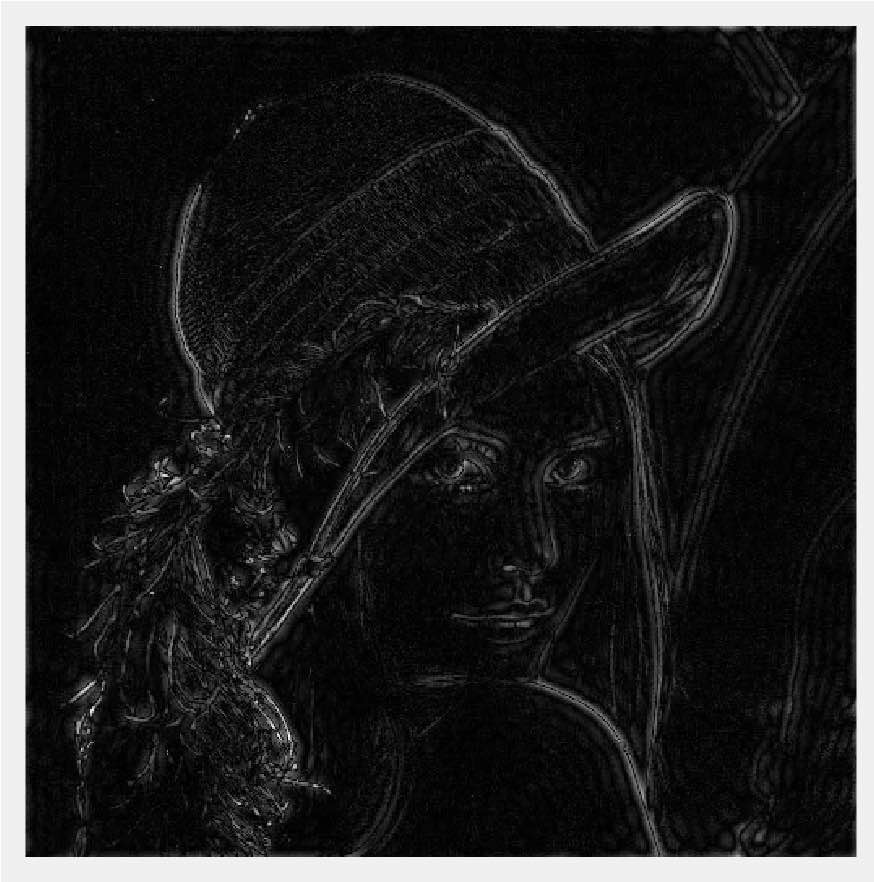
Maintenant on applique la DCT :

% Appliquer la transformée en cosinus discrète (DCT)
lena_dct = dct2(double(lena));

% Créer un filtre pour extraire les hautes fréquences
high_pass_filter = ones(size(lena));
cutoff_frequency_high = 10; % Ajuster la fréquence de coupure pour les hautes fréquences
high_pass_filter(1:cutoff_frequency_high, 1:cutoff_frequency_high) = 0;

% Appliquer le filtre dans le domaine fréquentiel
lena_dct_high_pass = lena_dct .* high_pass_filter;

% Inverser la DCT pour obtenir l'image avec les hautes fréquences
lena_high_pass = idct2(lena_dct_high_pass);

% Créer un filtre pour extraire les basses fréquences
low_pass_filter = ones(size(lena));
cutoff_frequency_low = 50; % Ajuster la fréquence de coupure pour les basses fréquences
low_pass_filter(1:cutoff_frequency_low, 1:cutoff_frequency_low) = 0;

% Appliquer le filtre dans le domaine fréquentiel
lena_dct_low_pass = lena_dct .* low_pass_filter;

% Inverser la DCT pour obtenir l'image avec les basses fréquences
lena_low_pass = idct2(lena_dct_low_pass);

% Afficher les images résultantes
figure;
subplot(1, 3, 1);
imshow(lena);
title('Image originale');
subplot(1, 3, 2);
imshow(lena_high_pass, []);
title('Hautes fréquences extraites');
subplot(1, 3, 3);
imshow(lena_low_pass, []);
title('Basses fréquences extraites');


La transformation en cosinus, et en particulier la transformée en cosinus discrète (DCT), est une technique de transformation utilisée dans le domaine du traitement du signal et de l'image. Elle est similaire à la transformée de Fourier, mais elle utilise des cosinus pour représenter les composantes fréquentielles d'un signal ou d'une image. La DCT est largement utilisée dans la compression d'images, notamment dans des normes telles que JPEG.

Dans le contexte de la DCT appliquée à une image, les hautes fréquences représentent les variations rapides ou les détails fins, tandis que les basses fréquences représentent les variations lentes ou les zones homogènes de l'image. Les hautes fréquences sont généralement concentrées dans le coin supérieur gauche de la DCT, et les basses fréquences sont réparties dans le reste de l'image.

# Compression proche de la compression JPEG

1. Préparation de l'image

clc; % Efface la fenêtre de commande
clearvars; % Efface toutes les variables de l'espace de travail
close all; % Ferme toutes les fenêtres de figure ouvertes

% Lire l'image
img = imread('lena.bmp');

% Convertir l'image en niveaux de gris si elle n'est pas déjà en niveaux de gris
if size(img, 3) == 3
	img = rgb2gray(img);
end

% Découper l'image en blocs de 8x8 pixels et appliquer la DCT sur chaque bloc
dct_blocks = blockproc(double(img), [8 8], @(block) dct2(block.data));

% Appliquer la DCT inverse pour comparer le résultat à l'image initiale
reconstructed_img = blockproc(dct_blocks, [8 8], @(block) idct2(block.data));

% Afficher l'image originale et l'image reconstruite après DCT inverse
figure;
subplot(1, 2, 1);
imshow(img);
title('Image originale');
subplot(1, 2, 2);
imshow(uint8(reconstructed_img));
title('Image reconstruite après DCT inverse');


Lorsque l'on compare les deux images, celle de lena.bmp (l'image originale) et celle résultant de l'application de la DCT inverse, aucune différence n'est perceptible.

2. Quantification

Afin de faire la quantification selon $Q(i, j)=1+(1+i+j) \cdot / F$ et appliquer la chaîne inverse (déquantification et DCT inverse) pour différentes valeurs de F on ajoute ce code au code précèdent :

% La quantification
qualities = [10, 20, 50]; % Différentes valeurs de facteur de qualité
figure;

for i = 1:length(qualities)

	% Calculer la matrice de quantification Q
	F = qualities(i);
	Q = 1 + (1 + repmat((0:7)', 1, 8) + repmat(0:7, 8, 1)) / F;
	
	% Appliquer la quantification sur chaque bloc transformé en cosinus
	quantized_blocks = blockproc(dct_blocks, [8 8], @(block) round(block.data ./ Q));
	
	% Appliquer la déquantification et la DCT inverse
	dequantized_blocks = blockproc(quantized_blocks, [8 8], @(block) block.data .* Q);
	inverse_dct_blocks = blockproc(dequantized_blocks, [8 8], @(block) idct2(block.data));
	
	% Afficher l'image reconstruite après quantification et déquantification
	subplot(1, 3, i);
	imshow(uint8(inverse_dct_blocks));
	title(['Image après quantification (F = ' num2str(F) ')']);

end


On ne remarque pas de changement radical entre le facteur de qualité 10, 20 et 50.

3. Filtrage

On applique désormais un filtre conservant que les basses fréquences avec la matrice suivante :

| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |

On écrit à la suite du code précédent, le code suivant :

% Filtre pour ne conserver que les basses fréquences
filter = [
	1 1 1 0 0 0 0 0;
	1 1 0 0 0 0 0 0;
	1 0 0 0 0 0 0 0;
	0 0 0 0 0 0 0 0;
	0 0 0 0 0 0 0 0;
	0 0 0 0 0 0 0 0;
	0 0 0 0 0 0 0 0;
	0 0 0 0 0 0 0 0;
];

% Appliquer le filtre sur chaque bloc de la DCT quantifiée
filtered_blocks = blockproc(quantized_blocks, [8 8], @(block) block.data .* filter);

% Appliquer la déquantification et la DCT inverse
dequantized_filtered_blocks = blockproc(filtered_blocks, [8 8], @(block) block.data .* Q);
inverse_dct_filtered_blocks = blockproc(dequantized_filtered_blocks, [8 8], @(block) idct2(block.data));

% Afficher l'image originale et l'image filtrée
figure;
subplot(1, 2, 1);
imshow(uint8(reconstructed_img));
title('Image originale');
subplot(1, 2, 2);
imshow(uint8(inverse_dct_filtered_blocks));
title('Image filtrée');


Nous constatons une diminution de la qualité, mais aucune réduction de la taille n'est observée.