# Write up KCSC CTF 2023 (DONE 10/10)
---
## 1. Ez_Ceasar (Easy)
---
### Mô tả:
- Bài cung cấp flag đã được mã hóa bằng Caesar Cipher với bảng alphabet customed
- Challenge code:
```python
import string
import random
alphabet = string.ascii_letters + string.digits + "!{_}?"
flag = 'KCSC{s0m3_r3ad4ble_5tr1ng_like_7his}'
assert all(i in alphabet for i in flag)
key = random.randint(0, 2**256)
ct = ""
for i in flag:
ct += (alphabet[(alphabet.index(i) + key) % len(alphabet)])
print(f"{ct=}")
# ct='ldtdMdEQ8F7NC8Nd1F88CSF1NF3TNdBB1O'
```
### Lời giải:
- Vì bài không sử dụng alphabet 26 chữ cái nên chúng ta sẽ in thử bảng alphabet customed với chỉ số tương ứng:
```python
import string
alphabet = string.ascii_letters + string.digits + "!{_}?"
print(len(alphabet)) # len(alphabet) = 67
for i in range(68):
print(i, alphabet[i], sep = ' is ')
```
nhận được
```python
0 is a
1 is b
2 is c
3 is d
4 is e
5 is f
6 is g
7 is h
8 is i
9 is j
10 is k
11 is l
12 is m
13 is n
14 is o
15 is p
16 is q
17 is r
18 is s
19 is t
20 is u
21 is v
22 is w
23 is x
24 is y
25 is z
26 is A
27 is B
28 is C
29 is D
30 is E
31 is F
32 is G
33 is H
34 is I
35 is J
36 is K
37 is L
38 is M
39 is N
40 is O
41 is P
42 is Q
43 is R
44 is S
45 is T
46 is U
47 is V
48 is W
49 is X
50 is Y
51 is Z
52 is 0
53 is 1
54 is 2
55 is 3
56 is 4
57 is 5
58 is 6
59 is 7
60 is 8
61 is 9
62 is !
63 is {
64 is _
65 is }
66 is ?
```
- Sau khi nhận biết được từng chữ cái với chỉ số riêng, ta cần tìm được độ dịch chuyển (key) của bài. Mặc dù key là random nhưng ta có được format của cờ là 'KCSC{' nên có thể dễ dàng tìm được key dựa vào hai phương trình của chữ cái 'K' và 'C' đã được mã hóa thành 'l' và 'd'.
```
(36[K] + key)%67 = 11[l]
(28[C] + key)%67 = 3[d]
```
- Dễ dàng tìm ra được valid key là 42, từ đó chúng ta giải mã:
```python
ct = 'ldtdMdEQ8F7NC8Nd1F88CSF1NF3TNdBB1O'
pt = ''
for i in ct: pt += (alphabet[(alphabet.index(i) - 42) % 67])
print(pt)
```
> **Flag:**
> `KCSC{C3as4r_1s_Cl4ss1c4l_4nd_C00l}`
---
## 2. A3S_C1R (Easy)
---
### Mô tả:
- Bài cung cấp flag được mã hóa qua AES mode CTR
- Challenge code:
```python
from Crypto.Cipher import AES
from Crypto.Util import Counter
from Crypto import Random
flag = b'KCSC{s0m3_r3ad4ble_5tr1ng_like_7his}'
nonce = Random.get_random_bytes(8)
countf = Counter.new(64, nonce)
key = Random.get_random_bytes(32)
encrypto = AES.new(key, AES.MODE_CTR, counter=countf)
encrypted = encrypto.encrypt(b"TODO:\n - ADD HARDER CHALLENGE IN CRYPTO\n - ADD FLAG TO THE CHALLENGE\n")
encrypto = AES.new(key, AES.MODE_CTR, counter=countf)
encrypted2 = encrypto.encrypt(flag)
print(f"encrypted: {encrypted.hex()}")
print(f"encrypted2: {encrypted2.hex()}")
# encrypted: 5e07dfa19e2b256c205df16b349c0863a15839d056ada1fb425449f2f9af9563eccca6d15cb01aabbe338c851f7b163982127033787fff49e74e3e09f0aee048a1d5b29f5a
# encrypted2: 410bc8addf6036125f5fe17d4bb61c00ba565a9e71d1bf846f625eeac5bfa972f9e7c4fd60800ac9aa689f9b280f5a09fd3768674401ac60
```
### Lời giải:
- Vì bài thuộc dạng AES với mode CTR, phương thức là XOR plaintext với các key. Tuy nhiên do cả hai đoạn encrypted và encrypted2 đều reuse encrypto, ta có:
- xor(b"TODO:...", key) = encrypted
- xor(flag, key) = encrypted2
- Dựa vào tính chất của phép xor, ta dễ dàng recover flag bằng cách xor encrypted, encrypted2, flag với nhau.
```
A^B = B^A
A^(B^C) = (A^B)^C
A^0 = A
A^A = 0
```
- Code:
```python
from pwn import xor
encrypted1 = '5e07dfa19e2b256c205df16b349c0863a15839d056ada1fb425449f2f9af9563eccca6d15cb01aabbe338c851f7b163982127033787fff49e74e3e09f0aee048a1d5b29f5a'
encrypted2 = '410bc8addf6036125f5fe17d4bb61c00ba565a9e71d1bf846f625eeac5bfa972f9e7c4fd60800ac9aa689f9b280f5a09fd3768674401ac60'
tmp = b"TODO:\n - ADD HARDER CHALLENGE IN CRYPTO\n - ADD FLAG TO THE CHALLENGE\n"
e1, e2 = bytes.fromhex(encrypted1), bytes.fromhex(encrypted2)
print(xor(e1, e2, tmp))
```
nhận được:
```
b'KCSC{A3S_CTR_bU1_K1nd4_3asY_y0u_5h0uld_h4v3_s0lv3d_th1s}\xee\x00\xd6\xe7g\x8f\x9a\x16\xbb\xc4\x14\xa7\x1b'
```
> **Flag:**
> `KCSC{A3S_CTR_bU1_K1nd4_3asY_y0u_5h0uld_h4v3_s0lv3d_th1s}`
---
## 3. Is_it_CRT (Easy)
---
### Mô tả:
- Bài cho hint về CRT(vô nghĩa) và RSA(cho e - pub.expo) để giải flag.
- Challenge text:
```python
e = 65537
n1 = 130970791706695167120816954281347910242271741380848697030582097380414164464669582077501935100534315672736591163867589462360532537474343007717114862677036219839049659638193590918904482709879798794387701429067711189339541090962315499562919351155480834958649104605830303759610881412035697138279914413112238740763
n2 = 113641455496435721193134074028475386176456392079379291332104843107150260592574545964197594045447402797691233409140148854647138554130435281685396694982224051757694663968334285795059648876331981127831706285859528658283228869511829743448319293252496057080243050538084390601445944010478822202867577802474801791329
n3 = 115457592377723871442877828120043009812666552225344030925643785294781982752845765738712585283013530383946783306354281324295808919863405271857497036597560796067884303380890822753721631162428079111639955037289448237030785776123607750456878915823785099809072723104652279115157324089611136858768836165863398680203
c1 = 30205641158783357163061598073735588730679950235840534382941497051587980282400902972347912576505274818761099007699493094299366801627409654097234796805851040864489706974546874446811476122681874102134051059499515262761274274546668369933320015216502163383548510236101225370599258753560708068722034210162626804923
c2 = 7340742323302407330422449647684226850070712253152501455033801379382023949033438352721378237409230914162113993246249149771113074063922424514756305027050874444877721126264284642454264098887344586634403180691682203341368972229942120849177826057673408055065848316876227141406653440730644459969340909926030700535
c3 = 55645356229576991726290820253166125559920178689701167851283019943562627606690176220109383257847017836775793827103662981412236830329482802454580242635314923411008056558210411063545158619407523528841487658337051518783958350562281456553772083003206890498586599056920249966475452673566793925144997181076187273153
```
### Lời giải:
- Nhận thấy bài cho e (hint về RSA) và cho 3 cặp số (n, c), tuy nhiên flag là duy nhất nên chúng ta chỉ cần giải flag với một cặp (n, c).
- Somehow n1 không thể factor sử dụng factor.db, bên cạnh đó ta nhận thấy gcd(n1, n2) != 1 nên n1, n2 không là các số nguyên tố cùng nhau, điều đó chứng minh n1 có thể factor được bằng cách sử dụng gcd(n1, n2); từ đó ta tìm được ước nguyên tố p, q của n1.
```python
from numpy import gcd
p, q = gcd(n1, n2), n1//gcd(n1, n2)
```
nhận được
```python
p = 11353881877324711003979802139615058395337484069869327204614462296439884334893855149363852440127790628732414633471088851321186317538207960792596592119477097
q = 11535331538745540714738141702022923616940235271330067953307665528444215968500323164146763365026710855489137432279572472935140454733482859072047176027793379
```
đối với một bài RSA, tìm ra được p và q giúp ta dễ dàng giải mã flag:
```python
from Crypto.Util.number import long_to_bytes, inverse
fn = (p-1)*(q-1) #phi hàm euler
d = inverse(e, fn) #private key
pt = pow(c1, d, n1)
print(long_to_bytes(pt))
```
> **Flag:**
> `KCSC{N0t_Rea11y_4_CR1_4tt4ck_R1ght??!!??}`
### NOTE:
- Note 1: Chúng ta không nhất thiết phải tìm ra hai số p và q, chỉ cần một số p đã có thể giải quyết bài toán.
- Note 2: Phi hàm euler của p (fp) được sử dụng để đếm số các số nguyên tố cùng nhau với p, tuy nhiên trong bài, p là số nguyên tố nên fp = p-1.
- Note 3: Đối với Multiparty RSA (MR) như bài này, điều kiện cần của bài là n1, n2, n3 phải đôi một là hai số nguyên tố cùng nhau. Tuy nhiên đề bài không thỏa mãn nên ta có thể rút gọn các số n1, n2, n3 về gcd(n1, n2) , gcd(n2, n3), gcd(n3, n1).
- Dựa vào các note 1, 2, 3 ta có thể rút gọn công đoạn tính toán và tìm ra flag:
```python
f = gcd(n1, n2)-1
pt = pow(c1, inverse(e, f), gcd(n1, n2))
print(long_to_bytes(pt))
```
---
## 4. Ceasar_but_Harder!!!! (Medium)
---
### Mô tả:
- Bài cung cấp flag đã được mã hóa bằng Caesar Cipher với bảng alphabet customed (64 kí tự sau khi mất đi 3 kí tự bất kì).
- Challenge code:
```python
import string
import random
flag = "KCSC{s0m3_r3ad4ble_5tr1ng_like_7his}"
alphabet = string.ascii_letters + string.digits + "!{_}?"
assert all(i in alphabet for i in flag)
for i in range(3):
k = random.randint(0, len(alphabet))
alphabet = alphabet[:k] + alphabet[k+1:]
key = random.randint(0, 2**512)
ct = ""
for i in flag:
ct += (alphabet[(alphabet.index(i) + key) % len(alphabet)])
print(f"{ct=}")
# ct='2V9VnRcNosvgMo4RoVfThg8osNjo0G}mmqmp'
```
### Lời giải:
- Là bài khó hơn Ez_Ceasar nhưng vẫn dựa trên ý tưởng cũ, ta có được chỉ số trên bảng chữ cái raw (67 kí tự) tương ứng với known text là KCSC{}.
- KCSC{} ---> 2V9Vnp
- Như vậy:
- C(28) ---> V(47) ~ +19
- K(36) ---> 2(54) ~ +18
- S(44) ---> 9(61) ~ +17
- {(63) ---> n(13) ~ -50 ~ +17
- }(65) ---> p(15) ~ -50 ~ +17
- Nhận thấy bảng chữ cái bị khuyết đi ba kí tự bất kì nên độ dịch chuyển (k) bị giảm đi đúng 3 đơn vị, dễ dàng dự đoán:
- Chữ cái bị mất đầu tiên nằm trong (0, 28) | k = +20 ---> +19
- Chữ cái bị mất thứ ba nằm trong (36, 44) | k = +19 ---> +18
- Do vậy, tất cả các chữ cái từ [44, 66] đều dịch chuyển +17 hay -50
- Dựa vào đó, code:
```python
import string
alphabet = string.ascii_letters + string.digits + "!{_}?"
for i in range(44, 67):
print(i, 'from', alphabet[i%67], 'to', alphabet[(i+17)%67])
```
cho ra output:
```python
44 from S to 9
45 from T to !
46 from U to {
47 from V to _
48 from W to }
49 from X to ?
50 from Y to a
51 from Z to b
52 from 0 to c
53 from 1 to d
54 from 2 to e
55 from 3 to f
56 from 4 to g
57 from 5 to h
58 from 6 to i
59 from 7 to j
60 from 8 to k
61 from 9 to l
62 from ! to m
63 from { to n
64 from _ to o
65 from } to p
66 from ? to q
```
giúp ta thay thế được các kí tự có trong flag đã mã hóa, từ đó làm tương tự với hai khoảng (0,28) và (28, 36), thử các số ở hai cận kết hợp phán đoán các từ có trong flag, ta giải mã được cờ.
> **Flag:**
> `KCSC{y0u_be4t_My_C3A54R_bu7_HoW!!?!}`
---
## 5. Basic Math (Medium)
---
### Mô tả:
- Bài cung cấp flag sẽ được revealed sau 20 lần nhập đúng giá trị của x và h sao cho thỏa mãn phương trình.
- Challenge code:
```python
from Crypto.Util.number import getPrime
flag = b'KCSC{fake_flag}'
def verify(g, p, y, x, k, h):
return (y*x*pow(g, k, p)) % p == pow(g, h, p)
p = getPrime(256)
g = getPrime(128)
y = 65537
lst_x = []
lst_h = []
print(f"p = {p}")
print(f"g = {g}")
print(f"y = {y}")
try:
for i in range(20):
x = 0
h = 0
x = int(input("x = "))
h = int(input("h = "))
if x in lst_x or h in lst_h:
print('get out !!!')
exit(-1)
rs = verify(g, p, y, x, i, h)
if rs:
lst_x.append(x)
lst_h.append(h)
else:
print('get out !!!')
exit(-1)
flag = open('flag.txt', 'rb').read()
print(flag)
except:
print("something went wrong")
```
### Lời giải:
- Đối với bài, điều quan trọng là phải tìm được giá trị của x và h thỏa mãn. Bên cạnh đó, với phép toán mô-đun, một bài toán sẽ có rất nhiều kết quả (có nhiều x với mỗi h tương ứng). Vì vậy, ta cần phải tìm được liên hệ giữa x và h, qua đó giải và nhận cờ.
- Tuy nhiên, biến số i được thay đổi += 1 sau mỗi lần nhập kết quả chính xác; và hai giá trị (x, h) không được nhập lại nên cần phải lưu ý.
- Mở đầu bài toán, chúng ta cần giải phương trình: ```(y*x*pow(g, k, p)) % p == pow(g, h, p)```
- Từ đây ta có các phép biến đổi:
```
x * y * (pow(g, k, p)) ≡ g**h (mod p)
such that x * pow(g, k, p) ≡ inverse(y, p) * (g**h) (mod p) [Ta chuyển y sang VP được vì y và p là coprime]
such that x * (g**k) ≡ inverse(y, p) * (g**h) (mod p) [Có thể dùng assert để kiểm chứng biến đổi từ dòng trên xuống dòng dưới]
such that x ≡ inverse(y, p) * (g**(h-k)) (mod p)
- Đến được bước này, ta đã hoàn thành công việc tìm mối liên hệ giữa x và h, vì là phép mô-đun nên ta có thể chọn x tùy ý; ở đây chọn x = inverse(y, p)*pow(g, h-k) + p
- Tuy nhiên ta cần phải thay đổi hiệu h-k để (x, h) khác nhau qua mỗi lần nhập, vì vậy gọi delta = h-k, ta có code:
```
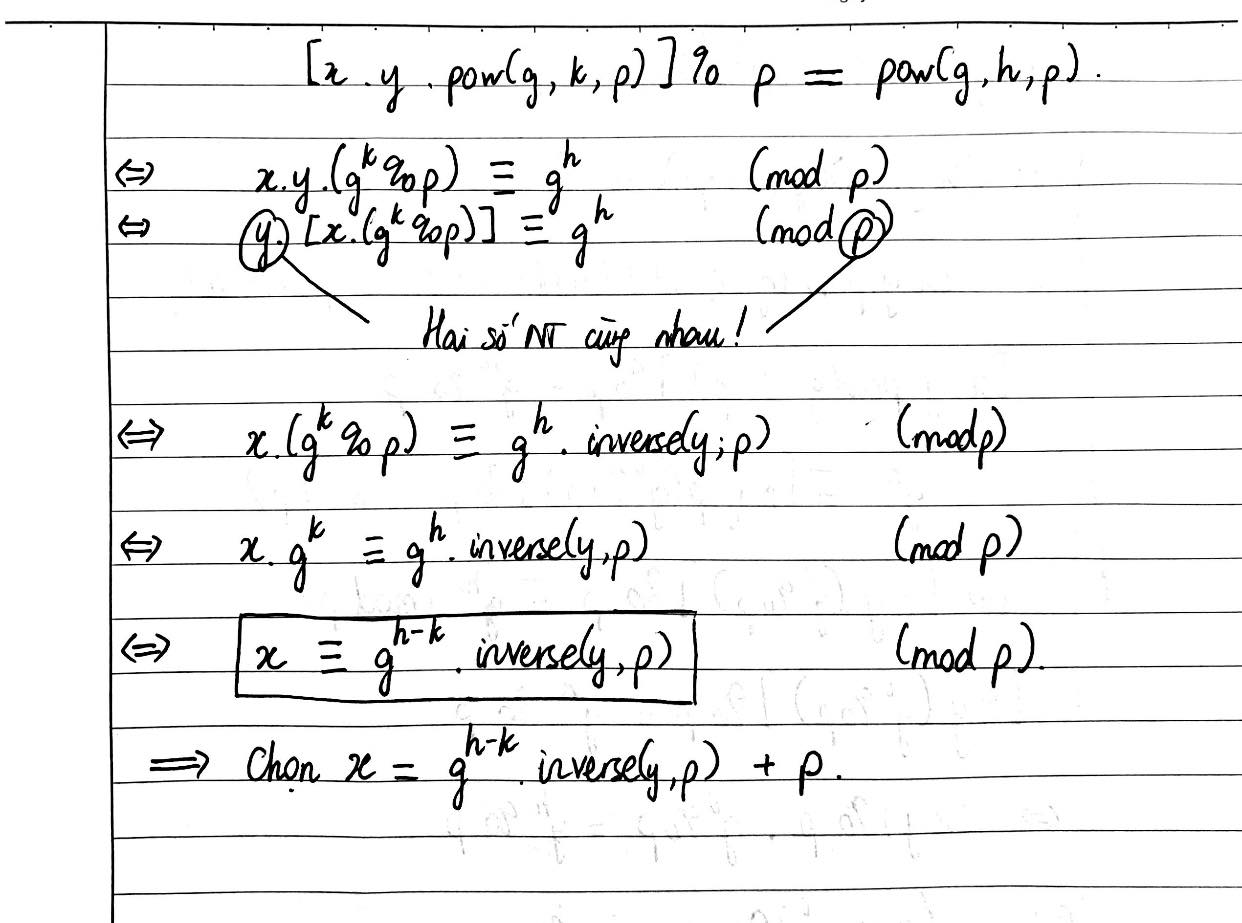
```python
from Crypto.Util.number import inverse
#p =
#g =
#y =
delta = 0
for i in range(20):
x = inverse(y, p)*pow(g, delta) + p
print(x, delta+i, end = '\n\n\n')
#assert (x*y*pow(g, i, p))%p == pow(g, delta+i, p)
delta += 1
```
- Kết nối với ```nc 103.162.14.116 16002```, ta nhận giá trị của p, g, y, thay vào code và nhận output, nhập các đáp án lần lượt và flag sẽ được trả về:
```b'KCSC{b4by_m4th_f0r_b4by_crypt0}'```
> **Flag:**
> `KCSC{b4by_m4th_f0r_b4by_crypt0}`
---
## 6. Qu4dr4t1c (Medium)
---
### Mô tả:
- Bài toán là một bài thuộc dạng RSA với n không thể factor
- Challenge code:
```python
from Crypto.Util.number import *
e = 65537
flag = b'KCSC{s0m3_r3ad4ble_5tr1ng_like_7his}'
def reverse(n):{
#function to reverse binary of n
}
while True:
p = getPrime(1024)
q = inverse(e, p)
if not isPrime(q):
continue
n = p * q
cipher = pow(bytes_to_long(flag),e,n)
n = reverse(n)
f = open('output.txt','w')
print(f"N = {n}",file=f)
print(f"e = {e}",file=f)
print(f"Cipher = {cipher}",file=f)
```
- Challenge text:
```python
N = 13524733362044232010736349595937464796777752381282044858904535549598695415259485540306280531287404403541039855661018351433654227342950710134306170544748441173774593898898768923907735212448495520658645896437678387670188401560165044043577269969416130117140222729708904953465161496726313677920240975640999580444678641072701612002184731572732086781180661428229265121878536891979130796853074814897843058889565035037987946761236280609366824566706376823708457581218333217098354233306312287549927586100725051273954453617494755601749327688591032955254157726764321151877093977335572150146339853526534429133266975640029987854181
e = 65537
Cipher = 3678620397255743852788853741107986108860981676309723331641730290544731009447106060307185476663548386172571801713658668783790148410569386488760778490944114348420614589196065297281576228195492339713201469195237426515519163981864121592862248581092535664172672153903696701157467812876812796524706730400133900257530235932000707810825149259236944828592989457788651053131965278448678769098840150302476398856999420129829083563611916558475165369663734941095660119099130765405955767410469621006246831917091632524062249541513097151767121519911807673852738866453379562168834013804186606786287157327927655505568604704262776577804
```
### Lời giải:
- Điều đầu tiên ta cần làm là giải quyết vấn đề N = reverse(n) (Đây là hàm đảo ngược các bit của n, ví dụ 8 = 1000 --> reverse(8) = 0001 = 1), từ đó thông qua xây dựng hàm ta tìm được:
```python
n = 10535928993957098707495868629894329792474452627850484364879975170776044359523502316712812160652468895360539480661909481847699725994424302337527894003647493404319479822948801135582064759413675137973329275363323307322700057229292876616227464768042846058603605698411497986428096602564579426872208940723176671431481552210121834864189396919386160623517904031927997144164227315481061780852236992136682820486583286833470123275605460358511115809814429237942992178881673308811386879602517751325668987352562850689002557168152549671137879638365209684530796460734176686377930364792278724956593791041667923647224672406278328787563
```
- Bước tiếp theo, nhận thấy n không thể factor nên vấn đề trở nên khó khăn hơn. Tuy nhiên, hint của bài là về phương trình bậc hai nên ta sẽ biến đổi để tìm p và q dựa vào dữ kiện q = inverse(e, p):
```
e*q = 1 (mod p) nên
e*q = k*p + 1 nên
e*q*p = k*p*p + p nên
k*(p**2) + p - e*n = 0
```
- Brute force bằng code tìm ra k:
```python
from gmpy2 import iroot
from Crypto.Util.number import *
i = 1
while True:
delta = iroot(1+4*i*e*n, 2)[0]
p = (-1+delta)//(2*i)
if isPrime(p) and n%p == 0:
print(p)
break
else: i += 1
```
- nhận được:
```python
p = 106245478298766053336506937865696693518495671128140728235840143567858412848196219487107562730423460350636088499018940205376906326308245092147076762614122387487384071498893733389141981647735797413890130062601671192092533177585198005584601980589160823077821937079776813122221838761636244752593026992533381924761
```
- Từ đây bài trở nên dễ dàng khi ta có thể tìm ra q, f(n), d và từ đó nhận được flag qua code:
```python
q = n//p
fn = (p-1)*(q-1)
d = inverse(e, fn)
pt = long_to_bytes(pow(ct, d, n))
print(pt)
```
> **Flag:**
> `KCSC{1f_D4m14n_g3t_m4rr13d_w1th_4ny4,th3_34st_4nd_th3_W3st_w1ll_b3_p34c3ful!!!!}`
---
## 7. Affinity (Medium)
---
### Mô tả:
- Bài mã hóa bằng thuật toán mã hóa Affine Cipher đã bị ẩn các biến a, b, n trong hàm mã hóa E(x) = (a*x +b) mod n.
- Challenge code:
```python
from Crypto.Util.number import getPrime, inverse, GCD
from random import randint
FLAG = b"KCSC{s0m3_r3ad4ble_5tr1ng_like_7his}"
print(ord('K'), ord('C'), ord('S'), ord('{'), ord('}'), ord('_'))
assert FLAG.startswith(b"KCSC{") and FLAG.endswith(b"}")
def caesar_affine(msg, key, p):
ct = []
for m in msg:
c = (m + key[0]) % p
c = (key[1]*c + key[2]) % p
ct.append(c)
return ct
enc = list(FLAG)
n = getPrime(32)
for i in range(32):
key = (randint(1,n), randint(1,n-1), randint(1,n))
enc = caesar_affine(enc, key, n)
# print(n) In your dream! :)
print(enc)
#ct = [1910234182, 2771761218, 1048707146, 2771761218, 871449803, 617943628, 2163740357, 1302213321, 2302873284, 3886794429, 1086831562, 2752699010, 1517595080, 3886794429, 1498532872, 3240649152, 2321935492, 3690474878, 3886794429, 2379122116, 364437453, 3886794429, 3006205185, 852387595, 3905856637, 364437453, 364437453, 3886794429, 4064051772, 2809885634, 2379122116, 3240649152, 149055694, 3886794429, 2125615941, 206242318, 3886794429, 3671412670, 3886794429, 1283151113, 2321935492, 1086831562, 3886794429, 168117902, 2752699010, 1302213321, 3886794429, 2771761218, 2752699010, 1517595080, 579819212, 598881420, 3886794429, 1086831562, 2752699010, 1517595080, 3886794429, 1283151113, 2752699010, 3886794429, 579819212, 852387595, 2321935492, 3690474878, 2302873284, 2302873284, 3202524736, 3202524736, 2302873284, 656068044]
```
### Lời giải:
- Thuật toán mã hóa của bài khá phức tạp khi hầu hết các thành phần đều là random, tuy nhiên ta có thể sử dụng biến đổi toán học để tìm ra format chuẩn cho hàm mã hóa của Affine:
```
c = (m + key[0])%n
c = (key[1]*c + key[2])%n
nên: c = (key[1]*(m + key[0]) + key[2])%n
hay c ≡ key[1]*m + key[0]*key[1] + key[2] (mod n)
với a = key[1]
và b = key[0]*key[1] + key[2]
```
- Dựa vào known text ta biết được các kí tự sau:
```python
K from 75 to 1910234182 (c1)
C from 67 to 2771761218 (c2)
S from 83 to 1048707146 (c3)
{ from 123 to 871449803 (c4)
```
- qua đó rút được 4 phương trình:
```
c1 ≡ 75*a + b (mod n)
c2 ≡ 67*a + b (mod n)
c3 ≡ 83*a + b (mod n)
c4 ≡ 123*a + b (mod n)
```
- suy ra hai phương trình con:
```
c2-c1 ≡ -8*a (mod n)
c4-c3 ≡ 40*a (mod n) ≡ (-5)*(-8*a) (mod n)
```
- hay:
```
c4-c3 ≡ (-5)*(c2-c1) (mod n) hay
c4-c3+5*(c2-c1) ≡ 0 (mod n)
```
- Từ đó tìm được ```n = c4-c3+5*(c2-c1)```, chọn n là số nguyên tố phù hợp, ta dễ dàng tìm được a và b sử dụng sagemath. Cuối cùng, ta đã có được a, b, n; sử dụng hàm giải mã D(E(x)) = (inverse(a, n)*(E(x) - b)) mod n ta nhận được flag.
- CODE:
```python
from Crypto.Util.number import *
ct = [1910234182, 2771761218, 1048707146, 2771761218, 871449803, 617943628, 2163740357, 1302213321, 2302873284, 3886794429, 1086831562, 2752699010, 1517595080, 3886794429, 1498532872, 3240649152, 2321935492, 3690474878, 3886794429, 2379122116, 364437453, 3886794429, 3006205185, 852387595, 3905856637, 364437453, 364437453, 3886794429, 4064051772, 2809885634, 2379122116, 3240649152, 149055694, 3886794429, 2125615941, 206242318, 3886794429, 3671412670, 3886794429, 1283151113, 2321935492, 1086831562, 3886794429, 168117902, 2752699010, 1302213321, 3886794429, 2771761218, 2752699010, 1517595080, 579819212, 598881420, 3886794429, 1086831562, 2752699010, 1517595080, 3886794429, 1283151113, 2752699010, 3886794429, 579819212, 852387595, 2321935492, 3690474878, 2302873284, 2302873284, 3202524736, 3202524736, 2302873284, 656068044]
pt = ''
c1 = 1910234182
c2 = 2771761218
c3 = 1048707146
c4 = 871449803
c5 = 656068044
c6 = 3886794429
n = c4-c3+5*(c2-c1)
a, b = 1957498039, 3791483389
a_inv = inverse(a, n)
f = lambda x : a_inv*(x - b) % n
for i in ct: pt += chr(f(i))
print(pt)
```
> **Flag:**
> `KCSC{Wow!_y0u_be4t_m3_Thr33_7ime5_In_a_d4y_H0w_C0u1D_y0u_d0_1h4t!!??!}`
---
## 8. R54 (Medium)
---
### Mô tả:
- Challenge code:
```python
from Crypto.Util.number import *
import hashlib
p = getPrime(1024)
q = getPrime(1024)
n = p*q
print(n)
e = 65537
flag = b'KCSC{s0m3_r3ad4ble_5tr1ng_like_7his}'
m = len(flag)
if m%2:
flag+= bytes(0x01)
def dbytes2int(b):
return b[0]*256+b[1]
ciphertxt = b''
for i in range(0, len(flag), 2):
plt = dbytes2int(flag[i:i+2])
c = pow(plt,e,n)
# print(c)
h = hashlib.sha256(long_to_bytes(c)).hexdigest()
k = bytes.fromhex(h[:8])
# print(h)
ciphertxt += k
# print(ciphertxt)
with open("./Chall_med_4/enc_msg.bin", "wb") as f:
f.write(ciphertxt)
# n = 20675528040670526996752940893288629654073674678976458593562885254372323957903532876778575683971980608430988271483012687068546409103618011471627912308716870404710200387846081948584012645579489130659361868569525868828863142513688732813453572263121568340255562594977295513766156580889393986895191199436845252360294885224181350174035317346113446210888214332389015986819447524673296950196284975878585211748477505072532061859389809017849787533731620947172314201145532242513117285325664785809436379731158841381092296256976553945301076520532403729003821419792192809111636400447743715443579056636708987896016462504011033448823
```
### Lời giải:
- Sử dụng code:
```python
with open("enc_msg_fixed.bin", "rb") as f: print(f.read())
```
ta nhận được flag đã encrypted:
```
b'\xec\xa4\xb9K\xe6\xb9&}M\rO9\xad\xfd\xfe\x16\xbcN\xb0\x9b\x88\xf2\xac\xa8\xf1\x89\x8f\x81\x8fAT\\\xacI$a]\x82\xf3\xd7\xffn\xa1\xc0\xc9\x11\x06\xe5h?]q'
```
- Bài khó nhưng có thể Brute force từng **đôi kí tự** rồi check với dãy bytes trên, suy ra:
> **Flag:**
> `KCSC{r54_!5_51Mp3|_r1gH+?}`
---
## 9. Random (Medium)
---
### Mô tả:
- Bài có flag đã được encrypted bằng AES mode CBC.
- Challenge code:
```python
from cryptography.hazmat.backends import default_backend
from cryptography.hazmat.primitives import padding
from cryptography.hazmat.primitives.ciphers import Cipher, algorithms, modes
import random, time
import struct
with open('flag.txt', 'r') as f:
FLAG = f.read()
def aes_encrypt(key, plaintext, iv):
key = key.ljust(32)[:32]
plaintext = plaintext.encode()
iv = iv.encode()
padder = padding.PKCS7(128).padder()
padded_plaintext = padder.update(plaintext) + padder.finalize()
cipher = Cipher(algorithms.AES(key), modes.CBC(iv), backend=default_backend())
encryptor = cipher.encryptor()
ciphertext = encryptor.update(padded_plaintext) + encryptor.finalize()
return ciphertext
def aes_decrypt(key, ciphertext, iv):
key = key.ljust(32)[:32]
iv = iv.encode()
cipher = Cipher(algorithms.AES(key), modes.CBC(iv), backend=default_backend())
decryptor = cipher.decryptor()
padded_plaintext = decryptor.update(ciphertext) + decryptor.finalize()
unpadder = padding.PKCS7(128).unpadder()
plaintext = unpadder.update(padded_plaintext) + unpadder.finalize()
return plaintext.decode()
random.seed(int(time.time()/4))
iv = str(random.randint(10**(16-1), 10**16 - 1))
with open('/dev/random', 'rb') as f:
num = int.from_bytes(f.read(3), byteorder='little')
random.seed(num)
num = (num >> 1 << 1) | random.choice([0,1])
key = num.to_bytes(3, byteorder='little')
cipher_text = aes_encrypt(key, FLAG, iv)
cipher_text = ' '.join(f'{byte:02x}' for byte in struct.unpack(f'{len(cipher_text)}B', cipher_text))
print('cipher text:', cipher_text)
exit(0)
```
### Lời giải:
- Với AES mode CBC, ta cần tìm được key, ciphertext, iv rồi sử dụng hàm giải mã đã có sẵn để in ra flag.
- Với **iv**, seed sẽ được random dựa vào thời gian hiện tại. Vì là seed nên chúng ta chỉ cần sử dụng đúng hàm tương tự như source code là có thể nhận được **iv**:
```python
random.seed(int(time.time()/4))
iv = str(random.randint(10**(16-1), 10**16 - 1))
```
- Với **ciphertext**, bản mã trên server là bản mã đã bị thay đổi format nên ta cần phải chuyển ngược lại thành dạng đúng của **ciphertext**:
```python
cipher_text = '...'
ct = b''.join(struct.pack('B', int(byte, 16)) for byte in cipher_text.split())
```
- Cuối cùng, **key** là thành phần khó tìm nhất trong bài, đẩy độ khó lên thành medium. Với một số **num** bị ẩn đi hoàn toàn trong bài, code thực hiện ```random.seed(num)``` rồi tạo ra **key**:
```python
num = (num >> 1 << 1) | random.choice([0,1])
key = num.to_bytes(3, byteorder='little')
```
- Nhận thấy **num** là số int được chuyển từ 3 bytes nên giới hạn của **num** sẽ là ```[1, 2**24]```, đến đây chúng ta cần brute force rồi tìm ra chuỗi có chứa ```'KCSC{'```, khi đó flag sẽ được revealed hoàn toàn. Nhưng **num** được ```|``` với hoặc 0 hoặc 1 nên ta cần brute force với hai trường hợp riêng.
- Bên cạnh đó, hàm giải mã có thể được đơn giản hóa đi thành:
```python
def aes_decrypt(key, ciphertext, iv):
key = key.ljust(32)[:32]
iv = iv.encode()
cipher = Cipher(algorithms.AES(key), modes.CBC(iv), backend=default_backend())
decryptor = cipher.decryptor()
padded_plaintext = decryptor.update(ciphertext) + decryptor.finalize()
return padded_plaintext
```
- Ta có code (với trường hợp choice = 0):
```python
from pwn import *
from cryptography.hazmat.backends import default_backend
from cryptography.hazmat.primitives import padding
from cryptography.hazmat.primitives.ciphers import Cipher, algorithms, modes
import struct
def aes_decrypt(key, ciphertext, iv):
key = key.ljust(32)[:32]
iv = iv.encode()
cipher = Cipher(algorithms.AES(key), modes.CBC(iv), backend=default_backend())
decryptor = cipher.decryptor()
padded_plaintext = decryptor.update(ciphertext) + decryptor.finalize()
return padded_plaintext
random.seed(int(time.time()/4))
iv = str(random.randint(10**(16-1), 10**16 - 1))
s = remote("103.162.14.116", 16001)
print(iv, s.recv())
#iv = str(9032022690947522)
#cipher_text = '96 af 0a c3 a9 80 4e 54 ae 37 99 07 8e 90 06 1d 8f a9 57 d3 f2 d5 d4 0a 4f 60 30 49 5b 4d 38 16'
ct = b''.join(struct.pack('B', int(byte, 16)) for byte in cipher_text.split())
for num in range(1, 2**24):
random.seed(num)
num = (num >> 1 << 1) | 0
key = num1.to_bytes(3, byteorder='little')
pt = aes_decrypt(key, ct, iv)
if("KCSC{" in str(pt)):
print(pt)
break
```
- Với trường hợp choice = 1, ta làm tương tự.
- Nên thử trường hợp choice = 1 vì flag được giải bằng trường hợp này.
> **Flag:**
> `KCSC{Brut3_F0rc3_3asy_Pe4sy!}`
**NOTE:**
- Bài dễ gây nản nên thay vì sử dụng ```range(1, 2**24)``` thì ta nên chia thành các khoảng nhỏ hơn.
- Thử với ```range(2**20, 2**24)``` (Đây là đoạn tìm ra flag) để tránh mất thời gian.
---
## 10. No More Basic Math (Hard)
---
### Mô tả:
- Bài tách flag thành 2 phần, mã hóa chúng bằng thuật toán mã hóa riêng.
- Challenge code:
```python
from Crypto.Util.number import bytes_to_long
from random import getrandbits
# FLAG = b'KCSC{fake_flag}'
p = getrandbits(1024)
q = getrandbits(1024)
def encrypt(msg, key):
m = bytes_to_long(msg)
return p * m + q * (m**3 + m**2 + m) + (3*m + 2*p + q) * key
n = len(FLAG)
assert(n > 20)
key = getrandbits(1024)
print(f'n = {n}')
print(f'p = {p}')
print(f'q = {q}')
print(f'c1 = {encrypt(FLAG[:20], key)}')
print(f'c2 = {encrypt(FLAG[-20:], key)}')
'''
n = 30
p = 48762188199150535581975412897924691165761153794040728191647919999953750500528915467941977942434049609148928874111418540791659239318033502960490438029918494978450003766475054277305000975826296521110691624198929727387822917181466972531783670424803605073382160801015364428887438227795060240461156343151628730113
q = 123154173062875129803388789468997467602861692189899574796521281322028039797350493630230549858629977130216821188366984746616639200404382396043604419180869596904421472720201306121199119571368299417757494448400590479108311324077855468994881760593143713996410859474408904326793393402741912427742694768217550181270
c1 = 21361708399259692476490585224474478239848096267728875151027667930547884138531321455258045949871008481309353774592024104870537486086028259415199204699193912434732702436520694573344765029331922878031532757006467986508373826559848018510846704694596043438688980012743479503379279444261834245820139438602646123909719216866856864573656625922211883930084371564748739048999645791127706355352400765930549436631488077615035313501456035704196655631076251694505647371287090426267130518184310327417676973790605083858188079554372289805772049887809199182600395727164328773350053287895190505219555434017220365550650906129322383481252
c2 = 21361708399259692476490585224474478239848096267728875151027667930547884138531321455258045949871008481309353774592024104870537486086028259415199204699193912434732702462872923491616113323696576471401453366769073405539609186296897006352387813496579755357765019379630756911340195523429031527586036900468063337747524187687027790122248988574172180712302674206934331239449040784296700054535172565955515658035497532654412975186522396759714280936589419263016914222837327779108969285650803460583010919600081536939185789237255320735405198555005684445856588326590949453146466337908623498742769971401502687499945846050861617865180
'''
```
### Lời giải:
- Vì đề bài cho biết độ dài của flag, ta sẽ có hai hướng làm:
- [x] Sử dụng LLL
- [x] Sử dụng Coppersmith hai ẩn
#### Cách 1: LLL algorithm
- Để sử dụng LLL giải bài toán này, trước hết ta cần nhìn qua công thức mã hóa:
```python
c = p * m + q * (m**3 + m**2 + m) + (3*m + 2*p + q) * key
```
với `p`, `q`, key được random.
- LLL áp dụng cho hệ phương trình tuyến tính, vì vậy cần phải biến đổi phù hợp:
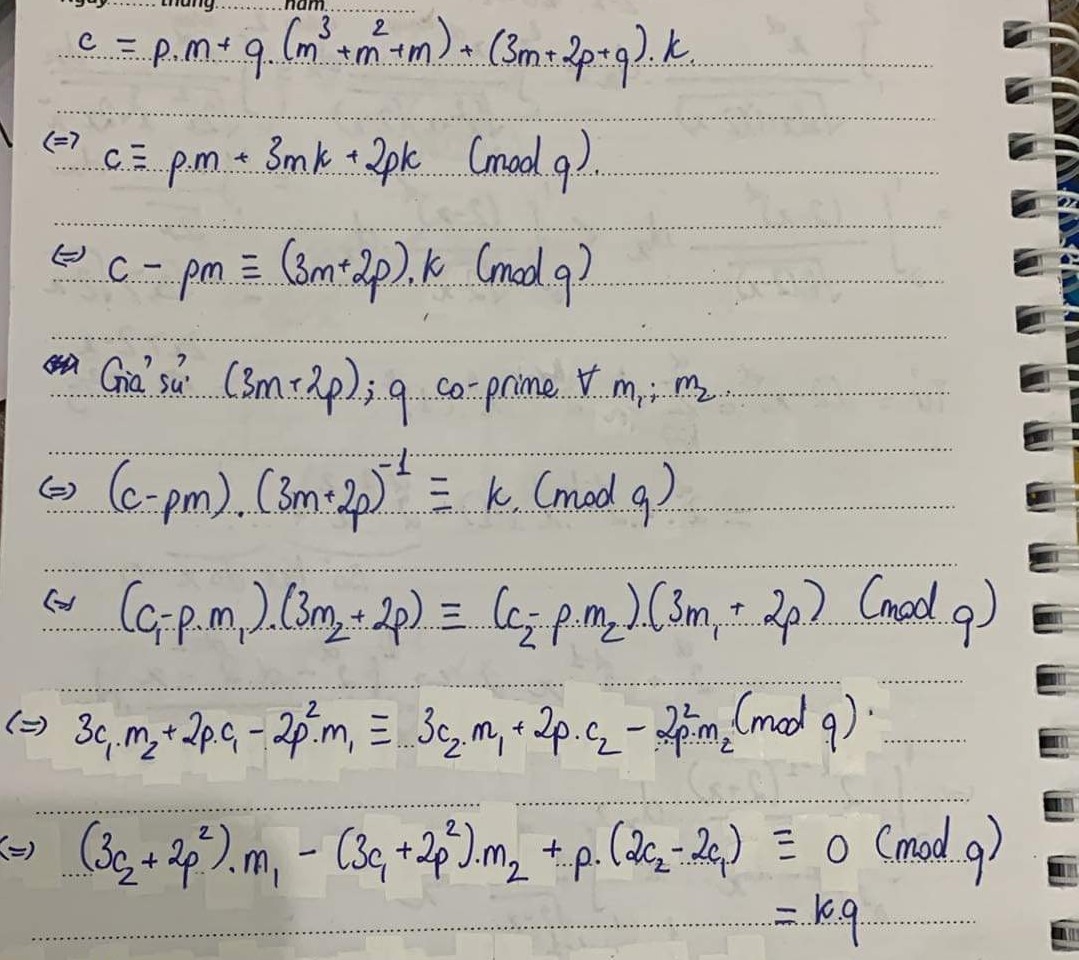
- Từ đây ta có thể thành lập các vector và ma trận tương ứng và giải bằng LLL trong sagemath.
- Code:
```python
from sage.all import *
from Crypto.Util.number import long_to_bytes
n = 30
p = 48762188199150535581975412897924691165761153794040728191647919999953750500528915467941977942434049609148928874111418540791659239318033502960490438029918494978450003766475054277305000975826296521110691624198929727387822917181466972531783670424803605073382160801015364428887438227795060240461156343151628730113
q = 123154173062875129803388789468997467602861692189899574796521281322028039797350493630230549858629977130216821188366984746616639200404382396043604419180869596904421472720201306121199119571368299417757494448400590479108311324077855468994881760593143713996410859474408904326793393402741912427742694768217550181270
c1 = 21361708399259692476490585224474478239848096267728875151027667930547884138531321455258045949871008481309353774592024104870537486086028259415199204699193912434732702436520694573344765029331922878031532757006467986508373826559848018510846704694596043438688980012743479503379279444261834245820139438602646123909719216866856864573656625922211883930084371564748739048999645791127706355352400765930549436631488077615035313501456035704196655631076251694505647371287090426267130518184310327417676973790605083858188079554372289805772049887809199182600395727164328773350053287895190505219555434017220365550650906129322383481252
c2 = 21361708399259692476490585224474478239848096267728875151027667930547884138531321455258045949871008481309353774592024104870537486086028259415199204699193912434732702462872923491616113323696576471401453366769073405539609186296897006352387813496579755357765019379630756911340195523429031527586036900468063337747524187687027790122248988574172180712302674206934331239449040784296700054535172565955515658035497532654412975186522396759714280936589419263016914222837327779108969285650803460583010919600081536939185789237255320735405198555005684445856588326590949453146466337908623498742769971401502687499945846050861617865180
M = Matrix([
[1, 0, 0],
[0, 1, 0],
[0, 0, 1],
[0, 0, 0],
])
I = [[(3*c2 + 2*p*p)], [(3*c1 + 2*p*p)], [2*p*(c1 - c2)], [q]]
M = M.augment(matrix(I))
'''
In order to make
M = Matrix([
[1, 0, 0, (3*c2 + 2*p*p)],
[0, 1, 0, (3*c1 + 2*p*p)],
[0, 0, 1, 2*p*(c1 - c2)],
[0, 0, 0, q],
])
'''
L = M.LLL()
m1, m2 = long_to_bytes(abs(L[0][0])), long_to_bytes(abs(L[0][1]))
m1, m2 = bytes.decode(m1, "utf-8"), bytes.decode(m2, "utf-8")
pt = m1[:10] + m2
print(pt)
```
- Do `flag` được chia làm hai phần `m1`, `m2` bao gồm cả phần overlap nên chúng ta sẽ viết `pt` như trên để nhận được flag hoàn chỉnh.
#### Cách 2: Coppersmith hai ẩn
- Với phương trình tương tự như trên, ta lập phương trình với hai ẩn.
- Code:
```python
from Crypto.Util.number import long_to_bytes
from sage.all import *
import itertools
def defund_multivariate(f, bounds, m=1, d=None):
if not d:
d = f.degree()
R = f.base_ring()
N = R.cardinality()
#f /= f.coefficients().pop(0)
f = f.change_ring(ZZ)
G = Sequence([], f.parent())
for i in range(m+1):
base = N^(m-i) * f^i
for shifts in itertools.product(range(d), repeat=f.nvariables()):
g = base * prod(map(power, f.variables(), shifts))
G.append(g)
B, monomials = G.coefficient_matrix()
monomials = vector(monomials)
factors = [monomial(*bounds) for monomial in monomials]
for i, factor in enumerate(factors):
B.rescale_col(i, factor)
B = B.dense_matrix().LLL()
B = B.change_ring(QQ)
for i, factor in enumerate(factors):
B.rescale_col(i, 1/factor)
H = Sequence([], f.parent().change_ring(QQ))
for h in filter(None, B*monomials):
H.append(h)
I = H.ideal()
if I.dimension() == -1:
H.pop()
elif I.dimension() == 0:
roots = []
for root in I.variety(ring=ZZ):
root = tuple(R(root[var]) for var in f.variables())
roots.append(root)
return roots
return []
n = 30
p = 48762188199150535581975412897924691165761153794040728191647919999953750500528915467941977942434049609148928874111418540791659239318033502960490438029918494978450003766475054277305000975826296521110691624198929727387822917181466972531783670424803605073382160801015364428887438227795060240461156343151628730113
q = 123154173062875129803388789468997467602861692189899574796521281322028039797350493630230549858629977130216821188366984746616639200404382396043604419180869596904421472720201306121199119571368299417757494448400590479108311324077855468994881760593143713996410859474408904326793393402741912427742694768217550181270
c1 = 21361708399259692476490585224474478239848096267728875151027667930547884138531321455258045949871008481309353774592024104870537486086028259415199204699193912434732702436520694573344765029331922878031532757006467986508373826559848018510846704694596043438688980012743479503379279444261834245820139438602646123909719216866856864573656625922211883930084371564748739048999645791127706355352400765930549436631488077615035313501456035704196655631076251694505647371287090426267130518184310327417676973790605083858188079554372289805772049887809199182600395727164328773350053287895190505219555434017220365550650906129322383481252
c2 = 21361708399259692476490585224474478239848096267728875151027667930547884138531321455258045949871008481309353774592024104870537486086028259415199204699193912434732702462872923491616113323696576471401453366769073405539609186296897006352387813496579755357765019379630756911340195523429031527586036900468063337747524187687027790122248988574172180712302674206934331239449040784296700054535172565955515658035497532654412975186522396759714280936589419263016914222837327779108969285650803460583010919600081536939185789237255320735405198555005684445856588326590949453146466337908623498742769971401502687499945846050861617865180
Zmodq = Zmod(q)
PR.<m1, m2> = PolynomialRing(Zmodq, 2)
f = (3*c2 + 2*p*p)*m1 - (3*c1 + 2*p*p)*m2 + 2*p*(c2 - c1)
temp = defund_multivariate(f, bounds=(2**20, 2**20), m=1, d=2)
m1 = long_to_bytes(int(temp[0][0]))
m2 = long_to_bytes(int(temp[0][1]))
pt = m1[:10] + m2
print(pt)
```
> **Flag:**
> `KCSC{cant_take_my_3y3s_0f_LLL}`