【LeetCode】 1319. Number of Operations to Make Network Connected

Description

There are n computers numbered from 0 to n - 1 connected by ethernet cables connections forming a network where connections[i] = [a_i, b_i] represents a connection between computers a_i and b_i. Any computer can reach any other computer directly or indirectly through the network.
You are given an initial computer network connections. You can extract certain cables between two directly connected computers, and place them between any pair of disconnected computers to make them directly connected.
Return the minimum number of times you need to do this in order to make all the computers connected. If it is not possible, return -1.

Constraints:

• 1 <= n <= 105
• 1 <= connections.length <= min(n * (n - 1) / 2, 105)
• connections[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• There are no repeated connections.
• No two computers are connected by more than one cable.

有 n 台電腦分別被編號為 0 到 n - 1，且他們被電纜線連接成一個網路，一段連接 connections[i] = [a_i, b_i] 代表電腦 a_i 和 b_i 之間的連接。所有電腦可以透過網路直接或間接地探索到任何其他電腦。
給你一個初始的電腦網路 connections。你可以拔除兩台有連接的電腦之間的電纜，並且將電纜放回任何一對未連接的電腦將其連接。
回傳當所有的電腦都連接時，你拔除並重接電纜的最小次數。如果這不可能做到，回傳 -1。

限制：

• 1 <= n <= 105
• 1 <= connections.length <= min(n * (n - 1) / 2, 105)
• connections[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• 不會有重複的連接。
• 不會有兩台電腦被超過一條的電纜連接。

Example:

Example 1:

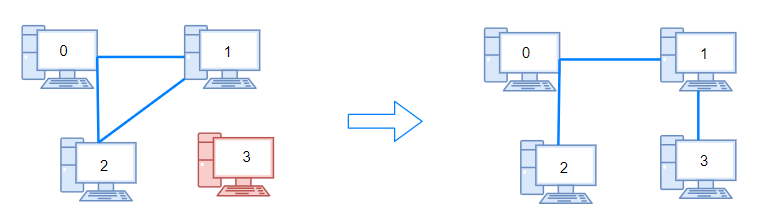
Input: n = 4, connections = [[0,1],[0,2],[1,2]]
Output: 1
Explanation: Remove cable between computer 1 and 2 and place between computers 1 and 3.

Example 2:

Input: n = 6, connections = [[0,1],[0,2],[0,3],[1,2],[1,3]]
Output: 2

Example 3:

Input: n = 6, connections = [[0,1],[0,2],[0,3],[1,2]]
Output: -1
Explanation: There are not enough cables.

Solution

• 兩個核心概念
  • 如果電腦數量為 n，當電纜數量大於 n - 1 時必定可以全連接；反之則無法連接，直接回傳 -1
  • 將本來就連接的電腦視為同一組，如果組別數量為 g，答案為 g - 1
    • 把一個組別視為一台電腦，把每一組連起來就達到全部電腦都連接
• 使用 DFS 遍歷電腦，有幾個 root node 代表有幾個組別
• 實作上需要注意
  • 原先給的連接表示法使用連接對，在 DFS 不好處理，因此先轉換為矩陣表示法
  • 矩陣表示法原本使用 vector<vector<int>> 儲存，但發現會吃 TLE 過不了，因此需要改為 vector<int>* 進行加速
  • DFS 需要記住電腦是否拜訪過，避免出現無窮迭代的錯誤

Code

class Solution {
public:
    void DFS(int now, vector<int>* to, vector<bool>& touched)
    {
        touched[now] = true;
        for(int i = 0; i < to[now].size(); i++)
            if(touched[to[now][i]] == false)
                DFS(to[now][i], to, touched);
    }

    int makeConnected(int n, vector<vector<int>>& connections) {
        
        if(n > connections.size() + 1)
            return -1;

        vector<int> to[n];
        for(int i = 0; i < connections.size(); i++)
        {
            to[connections[i][0]].push_back(connections[i][1]);
            to[connections[i][1]].push_back(connections[i][0]);
        }
        int g = 0;
        vector<bool> touched(n, false);
        for(int i = 0; i < n; i++)
        {
            if(touched[i] == false)
            {
                DFS(i, to, touched);
                g++;
            }
        }
        return g - 1;
    }
};

tags: LeetCode C++