###### tags: `資料結構` `Python`

# 資料結構 | 二元樹 | 使用 Python

:::info
此為學習筆記，如有錯誤請多指正，謝謝
:::

## 二元樹
二元樹 (Binary Tree)是一由有限節點組成的集合，集合可以為空的，或是樹根或是左右兩個子樹組成的。也就是一個節點最多只能有兩個子節點

以下是顆二元樹

## 二元搜尋樹
二元搜尋樹 (Binary Search Tree)，簡稱BST，之後都用BST來表示二元搜尋樹。

BST是符合左子樹必定比節點小，右子樹小必定比節點大的二元樹


這是顆BST，從原點來50來看，左子樹為30比較小，右子樹為70比較大。而底下的子樹都遵循著這規律

### 二元樹的資料表達方式
一般來說，我們使 **鏈結串列 Linked list** 來表示一棵樹

一個節點最基本必須要有以下三個屬性，分別代表節點本身的`value`，和左右兩個子節點的地址

class node:
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None
        # 其他屬性(可選)
        self.parent = None # 節點的父節點，如果為root指向None
        self.height = 1 # 節點的高度
        self.depth = 1 # 節點的深度

### 用一元陣列表示二元樹
二元數也可用陣列來表示
如果把上面的二元樹轉換成一元陣列

binary_tree = [None, 15, 10, 20, 8, 12, 18, 25]

我們從上面的例子可以知道

1. 索引值`0`不表示任何節點
2. 左子樹的索引值是 `父節點索引值 * 2`
3. 右子樹的索引值是 `父節點索引值 * 2 + 1`

### 樹的種類和搜尋效率
樹的搜尋效率和樹的形狀有很大的正相關，時間複雜度在計算機科學是最常被用在描述一段**演算法的效率**

時間複雜度假定的情況都在**如果這段演算法最糟糕可能要花多久**的背景下去定義的

下圖被稱為 `BigO` 常被用來表示時間複雜度，X軸表示資料的規模，Y軸為所花費時間


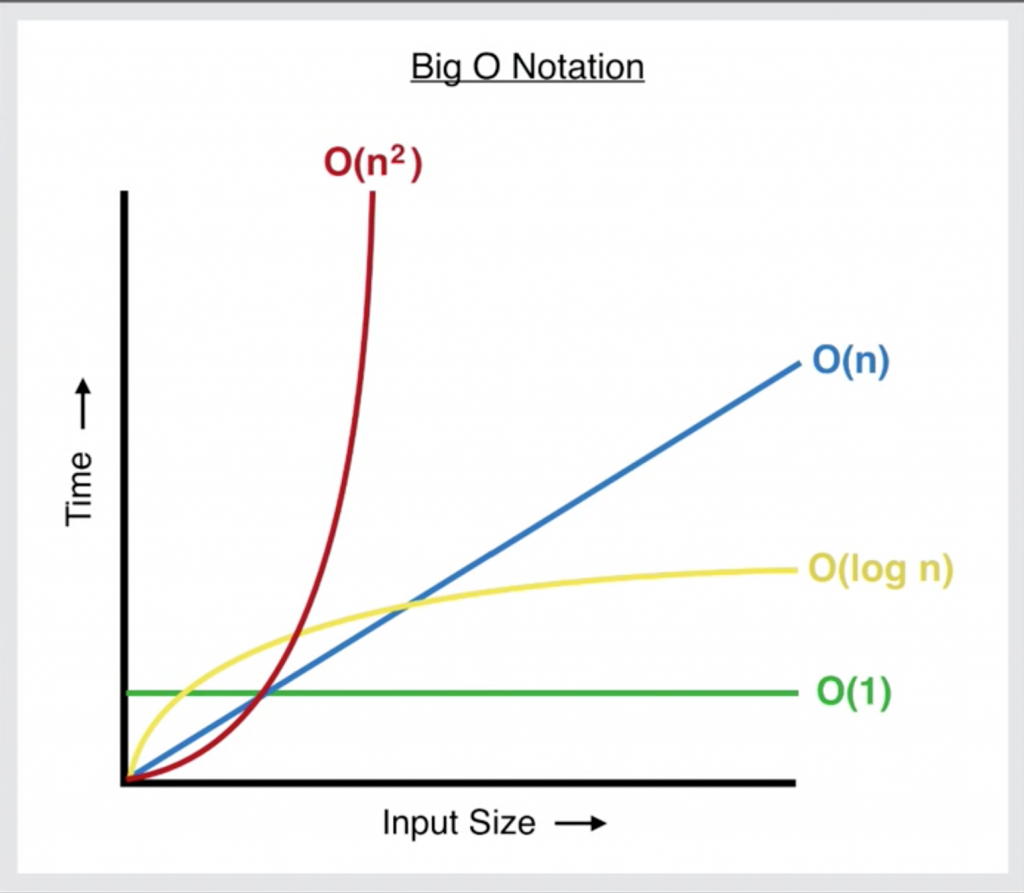
#### 完美二元樹(Fully Binary Tree)
當一顆深度為 $k$ 的二元樹，當節點數量為 $2^k-1$ 時候，稱為完美二元樹。特點是每層節點數量都是最大


完美二元樹的的樹的搜尋效率為 $O(log n)$。比較大小次數為該樹的深度

#### 歪斜樹(Skuwed Binary Tree)
歪斜樹如同其名是歪斜的二元樹，而可以分成向左歪斜或是向右歪斜


歪斜樹的搜尋效率為 $O(n)$ 是二元樹中效率最低的

## BST的實作

二元樹的新增也是要符合 `BST` 的規則，也就是根據這段值相比，大的右邊，小的左邊，不考慮是否有無重複的值

實作一個最基本的 BST 的步驟包含但不限於以下步驟
1. 節點的 `Class`
2. `BST Class` 的新增
3. `BST Class` 的刪除

### 節點

首先先創件個類表示節點，必須含有以下
1. `Left`。指向較小的節點
2. `Right`。指向較大的節點
3. `Value`。這節點的值，具有唯一性

接下來的都是可選
1. `Height`。可以實作 `AVL Tree`
2. `Parent`。指向父節點

class Node:
    def __init__(self, value=None) -> None:
        self.value = value
        self.left = None
        self.right = None
        self.parent = None # 節點的父節點
        self.height = 1 # 節點在樹中的高度

### 新增

`BST` 需要起點表示根節點 ( root )

class Binary_search_tree:
    def __init__(self) -> None:
        self.root = None

基本上可以利用迴圈或是遞迴來走訪節點，這裡採用遞迴來走訪

class Binary_search_tree:
    def __init__(self) -> None:
        self.root = None

    def insert(self,value) -> None:
        if self.root == None:
            self.root = Node(value)
        else:
            self._insert(value, self.root)

    def _insert(self, value, cur_node) -> None:
        #* 如果 insertValue < 當前節點，往左走 
        if cur_node.value > value:
            
            #* 如果節點為 None 表示不存在，創建新節點
            if cur_node.left == None:
                cur_node.left = Node(value)
                cur_node.left.parent = cur_node
                
            #* 表示存在節點，繼續往下走訪
            else:
                self._insert(value, cur_node.left)

                
        #* 如果 insertValue > 當前節點，往右走
        elif cur_node.value < value:
            
            #* 如果節點為 None 表示不存在，創建新節點
            if cur_node.right == None:
                cur_node.right = Node(value)
                cur_node.right.parent = cur_node
                
            #* 表示存在節點，繼續往下走訪
            else:
                self._insert(value, cur_node.right)
        #* 都無法比較表示節點已存在
        else:
            print('已存在節點')

### 刪除
刪除並沒有像新增一樣方便，手續甚至還有點繁多。這是因為樹是彼此互相串連的關係，假設一個節點斷掉，可能導致後續的資料遺失。可以想像成一段香腸如果從中間截斷，會導致後面的香腸也跟著不見

刪除會根據**是否有無子節點**有三種類型的刪除方法
1. 子節點數為 0
2. 子節點數為 1
3. 子節點數為 2

class Binary_search_tree:
    def __init__(self) -> None:
        self.root = None

    def delete(self, value):
        return self._delete(self.find(value))
    
    def _delete(self, node):
        if node == None: return

        #* 計算該節點的子節點數量
        def number_of_children(node):
            number = 0
            if node.left != None: number += 1
            if node.right != None: number +=1
            return number

        parent = node.parent
        num_child = number_of_children(node) # 子節點的數量
        
    ### 以下接續 ###

#### 子節點數為 0

代表該節點位於末端，直接刪除即可

#TODO 沒有child，就刪除節點
if num_child == 0:
    # 是否是根結點 (root)
    if parent == None: 
        self.root = None
        
    else:
        # 確認該節點位於父節點的左還是右，然後刪除
        if parent.left == node: 
            parent.left = None
        else:
            parent.right = None
    return

#### 子節點數為 1

當有一個子節點時，直接讓子節點代替該節點即可

#TODO 1個child，直接讓子節點篡位
if num_child == 1:
    # 確認子節點的在左還是右
    child = node.left if node.left != None else node.right

    # 刪除的節點如果為根結點 ( root )，子節點直接成為根結點
    if parent == None: 
        self.root = child
        
    else:
        # 確認該節點的位置在左還是右
        if parent.left == node: 
            # 替換成子節點
            parent.left = child 
            child.parent = parent
        else:
            parent.right = child 
            child.parent = parent   

#### 子節點數為 2

如果子節點數量為2，不能直接用子節點來代替。最佳的辦法為**最相近的節點**來替代

具體作法如下圖所示，假設要刪除 30 這節點，可以拿**右子樹的最小值**31；或**左子樹的最大值**25來代替該節點

以下使用右子樹的最小值

#TODO 2個child，獲取要刪除節點右節點的最小值或是左節點的最大值，並代替刪除的節點
if num_child == 2:
    successor = get_min_value(node.right) # 獲取右子樹的最小值，先稱篡位者
    node.value = successor.value # 篡位節點
    self._delete(successor) # 刪除原本篡位者的位置
    
    
# 獲取右子樹的最小值
def get_min_value(node):
    current = node
    while current.left != None: # 使用迴圈來獲取最小值
        current = current.left
    return current

## BTS實作的完整代碼

class Node:
    def __init__(self, value=None) -> None:
        self.value = value
        self.left = None
        self.right = None
        self.parent = None # 節點的父節點
        self.height = 1 # 節點在樹中的高度


class Binary_search_tree:
    def __init__(self) -> None:
        self.root = None

    def insert(self,value) -> None:
        if self.root == None:
            self.root = Node(value)
        else:
            self._insert(value, self.root)

    def _insert(self, value, cur_node) -> None:
        #* 如果 insertValue < 當前節點，放左邊 
        if cur_node.value > value:
            if cur_node.left == None:
                cur_node.left = Node(value)
                cur_node.left.parent = cur_node
            else:
                self._insert(value, cur_node.left)

        #* 如果 insertValue > 當前節點，放右邊 
        elif cur_node.value < value:
            if cur_node.right == None:
                cur_node.right = Node(value)
                cur_node.right.parent = cur_node
            else:
                self._insert(value, cur_node.right)
        else:
            print('已存在節點')

    def delete(self, value):
        return self._delete(self.find(value))
    

    
    def _delete(self, node):
        if node == None: return

        #* 計算該節點的子節點數量
        def number_of_children(node):
            number = 0
            if node.left != None: number += 1
            if node.right != None: number +=1
            return number
        

        def get_min_value(node):
            current = node
            while current.left != None:
                current = current.left
            return current

        parent = node.parent
        num_child = number_of_children(node)

        #TODO 沒有child，就刪除節點
        if num_child == 0:
            if parent == None: # 代表 root
                self.root = None
            else:
                if parent.left == node: # 確認節點的位置並從父節點刪除
                    parent.left = None
                else:
                    parent.right = None
            return

        #TODO 1個child，直接讓子節點篡位
        if num_child == 1:
            child = node.left if node.left != None else node.right

            if parent == None: # 刪除的節點如果為 root，子節點篡位
                self.root = child
            else:
                if parent.left == node: # 確認被刪除節點的位置，子節點直接篡位
                    parent.left = child
                    child.parent = parent
                else:
                    parent.right = child 
                    child.parent = parent   
    
        #TODO 2個child，獲取要刪除節點右節點的最小值或是左節點的最大值，並代替刪除的節點
        if num_child == 2:
            successor = get_min_value(node.right)
            node.value = successor.value # 篡位該節點
            self._delete(successor) # 刪除該節點原本的位置