* # quiz 3
###### tags:`sysprog2019`
contributed by < `YenHengLin` > < `xl86305955` >
# 深度學習
contributed by < `xl86305955` >
###### tags:`sysprog2019`

:::success
2004 年上映的[機械公敵(I, Robot)](https://zh.wikipedia.org/wiki/%E6%A9%9F%E6%A2%B0%E5%85%AC%E6%95%B5_(%E9%9B%BB%E5%BD%B1)) 中,在 2035年智慧型機器人作為人類的工具與夥伴佔據了人類十分重要的位置。近年 GPU 的快速發展,使得計算速度大幅提升;再加上 AlphaGo 的成功再次帶動了人工智慧的風潮,各類型的應用大鳴大放。例如:自駕車、人臉辨識應用等等。機械公敵中的智慧型機器人在當時看似遙不可及,但在人工智慧高速發展下這些在當時的"科幻電影"中的內容似乎近在咫尺。
:::
## 人工智慧史
### 人工智慧的誕生
### 第一次低潮
### IBM 深藍
### ImageNet
---
## 人工智慧 機器學習 深度學習
* 人工智慧、機器學習、深度學習這三者關係就如同下圖為一種包含關係
* 人工智慧是最外面的那塊圓,大約在 1950 時人類有了這個願景,希望機器能夠像人類般學習
* 機器學習則是實現人工智慧的方式,透過設計的演算法,使機器接收大量資訊後能夠漸漸完成一些工作。eg. 影像辨識、聲音辨識
* 深度學習則是機器學習中的一種方法。仿造人類大腦神經元相互連結傳遞資料,深度學習也透過一層一層的神經網路,透過每層神經元來傳遞訊息,最後達到機器學習的目的

參考資料:[人工智慧、機器學習與深度學習間有什麼區別?](https://blogs.nvidia.com.tw/2016/07/whats-difference-artificial-intelligence-machine-learning-deep-learning-ai/)
---
## 進入正題:深度學習
引用李宏毅教授:
>Deep Learning 就像把大象關進冰箱;打開冰箱門,把大象關進去,關上冰箱門,非常簡單。

###### 圖片來源:[Tutorial for General Deep Learning Technology](https://speech.ee.ntu.edu.tw/~tlkagk/slide/Tutorial_HYLee_Deep.pdf)
* Step 1: 挑選一個神經網路
* Step 2: 衡量這個網路的好壞
* Step 3: 從一大堆網路中挑出一個最好的網路
接下來會開始說明如何達成這三個步驟
----
## 感知器
* 1957 年由 Frank Rosenblatt 提出感知器 (Perceptron) 的概念,奠定了之後神經網路的基礎
### 感知器運作
如下圖所示,圖中的圓圈即是感知器,或可稱為神經元。其中 $x_1$, $x_2$ 為輸入,$w_1$, $w_2$ 則為兩個輸入對應之權重。輸出 $y$ 則是根據 $w_1x_1+w_2x_2$ 之值與 $\theta$ 做比較,若小於等於 $\theta$ 則輸出 $0$;反之則輸出 $1$

各個感知器皆擁有各輸入的權重及 $\theta$ 值。權重與 $\theta$ 是兩個非常重要的元素,由權重大小能夠決定一個輸入的重要性。權重越高,則代表輸入的訊號越重要,反之。而 $\theta$ 可以想成是一個臨界值,透過 $\theta$ 區隔出最終輸出。若 $\theta$ 越大則要使輸出為 $1$ 的門檻越高。
我們可以將 $\theta$ 另為 $-b$,利用移項將上述算式稍加改寫,其中 $b$ 稱作 `bias`,作用與 $\theta$ 一樣皆是作為一個臨界值。若 $b$ 為 $-0.01$,$b'$ 為 $-10$,則 $b$ 的門檻較 $b'$低,較容易達到輸出為 $1$
$y =
\begin{cases}
0,&\text{if}&w_1x_1 + w_2x_2 + b\leq 0 \\
1,&\text{if}&w_1x_1 + w_2x_2 + b> 0
\end{cases}$
### 感知器運用
考慮 NAND Gate 之真值表:
| $x_1$ | $x_2$ | $y$ |
| -------- | -------- | -------- |
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
使用座標表示:

根據感知器的運作,我們可以在座標上找到一組 ($w_1$, $w_2$, $b$) 使得我們的輸入符合真值表的特性。其中 $y = w_1x_1+w_2x_2+b$ 即是一條直線將輸出區分開來,當然符合輸出的直線具有無限多條。

>在直線下方區域皆符合輸出為 $1$
假設 ($w_1$, $w_2$, $b$) 分別為 ($-0.5$, $-0.5$, $0.7$),中間波浪符表示結果決定輸出零或一。以 C 語言模擬感知器行為:

```clike=
/* NAND Gate Perceptron */
struct perceptron {
float w1;
float w2;
float bias;
};
int nand_gate (int x1, int x2) {
float out;
struct perceptron nand;
nand.w1 = -0.5;
nand.w2 = -0.5;
nand.bias = 0.7;
out = x1*nand.w1 + x2*nand.w2 + nand.bias;
if (out <= 0)
out = 0;
else
out = 1;
return (int)out;
}
```
輸出結果:
```
(0,0) = 1
(0,1) = 1
(1,0) = 1
(1,1) = 0
```
:::info
或許會覺得,區區一個 NAND 閘可以搞出甚麼名堂。 NAND 閘可是萬用邏輯閘,舉凡 NOT、AND、XOR 閘等等,透過迪摩根定理皆可以透過 NAND 閘組合出來。由此即可做出加法器、 ALU等等,慢慢建構出 CPU。[nand2tetris](https://www.nand2tetris.org/) 就是透過 NAND 閘開始教你一步步達成這個目標。
:::
考慮 OR 之真值表:
| $x_1$ | $x_2$ | $y$ |
| -------- | -------- | -------- |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
使用座標表示。($w_1$, $w_2$, $b$) 分別為 ($-0.5$, $-0.5$, $0.2$),與 NAND 閘僅有 $b$ 之值不同:

根據不同的輸入,只要透過調整透過不同的 ($w_1$, $w_2$, $b$) 之值,即可得到想要的輸出,讓我們的感知器扮演著各式各樣不同的腳色。
### 感知器限制與突破
考慮 XOR 閘之真值表:
| $x_1$ | $x_2$ | $y$ |
| -------- | -------- | -------- |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
使用座標表示:

:::warning
Q: 找一條 $y = w_1x_1+w_2x_2+b$ 的直線來滿足真值表之輸出 ?
Ans : 找...找...不到
:::
就在前文提到能夠透過不同的 ($w_1$, $w_2$, $b$) 之值,使得感知器扮演不同的腳色,怎麼馬上就破功...
在 1969 年時提出了 XOR 閘無法用感知器表示之問題。感知器最大的限制就是僅能表現邏輯迴歸,而 XOR 閘的輸出找不到一條直線能夠滿足輸出。也因為只能表現邏輯迴歸的限制,因而推動了多層感知器的概念。於是大約在 1980s 時正式多層感知器正式被提出。
要解決 XOR 之問題有兩種解決方法:
#### 法一 : Feature Transformation
找到新的一組對應方式,將原先的座標值透過新的對應方式到新的座標

:::warning
問題 : 並非每次皆能找到一組好的對應方式
:::
#### 法二 : 透過感知器之組合
如果一個便當吃不飽,可以吃兩個。那如果一個感知器做不到,那可以用好多個嗎 ? 答案是可以的 !
我們可以利用 NAND、OR 及 AND 閘這些符合邏輯回歸特性的元件組合出與 XOR 閘一模一樣的輸出。

利用感知器表示,設定適當的權重與 bias ,使感知器扮演所需 之腳色。在第一部分的結果其實就是對 $x_1$ 及 $x_2$ 做特徵轉換,接著透過 AND 閘分類,決定輸出。

以 C 語言表示 :
```clike=
int nand_gate (int x1, int x2) {
float out;
struct perceptron nand;
nand.w1 = -0.5;
nand.w2 = -0.5;
nand.bias = 0.7;
out = x1*nand.w1 + x2*nand.w2 + nand.bias;
if (out <= 0)
out = 0;
else
out = 1;
return (int)out;
}
int or_gate (int x1, int x2) {
float out;
struct perceptron or;
or.w1 = 0.5;
or.w2 = 0.5;
or.bias = -0.2;
out = x1*or.w1 + x2*or.w2 + or.bias;
if (out <= 0)
out = 0;
else
out = 1;
return (int)out;
}
int and_gate (int x1, int x2) {
float out;
struct perceptron and;
and.w1 = 0.5;
and.w2 = 0.5;
and.bias = -0.7;
out = x1*and.w1 + x2*and.w2 + and.bias;
if (out <= 0)
out = 0;
else
out = 1;
return (int)out;
}
int xor_gate (int x1, int x2) {
int y1 = nand_gate(x1, x2);
int y2 = or_gate(x1, x2);
int out = and_gate(y1, y2);
return out;
}
```
輸出結果:
```
./xor
(0,0) = 0
(0,1) = 1
(1,0) = 1
(1,1) = 0
```
---
## 神經網路
:::info
利用感知器的相互組合,表現出預期的成果,看似沒甚麼問題。但是若是定義之問題較為複雜,需要較多的感知器、更多層的迭代,在設定參數產生對應之輸出將會成為一個大麻煩。因此神經網路最重要的一個性質之一就是: 根據輸入資料,自動更新參數以達到目的。
:::
### 神經元
所謂神經網路就是由大量的神經元所組合而成,而若干個神經元聚集成層,層與層之間互相傳遞訊號形成整個網路。下圖為神經元之圖示。每筆輸入 $x_i$ 乘上對應的權重 $w_i$ ,接著加上一個偏全值 $bias$ ,最後經過激勵函數 (Activation Function) 輸出 $y$ 為一個神經元的輸出。

### 基本神經網路架構 (Fully Connect Feedforward Network)
下圖為簡單神經網路之範例。層與層之間都是緊密相連,並以前一層的輸出作為自己的輸入。以下圖為例共分為三層,執行方向由左到右:
* 輸入層 (Input Layer): 以影像辨識為例,輸入層的輸入就是圖片。
* 隱藏層 (Hidden Layer): 隱藏層負責接收其上一層的輸出,經過計算之後再傳送給下一層作為輸入,最後輸出作為輸出層之輸入。隱藏層能夠視需求不停疊加,所謂的 "Deep" Learning,即是透過不段疊加隱藏層,營造出 夠 "深" 的網路。
* 輸出層 (Output Layer): 輸出最終結果,若是分類問題,則輸出可以是問題類別總和。

:::info
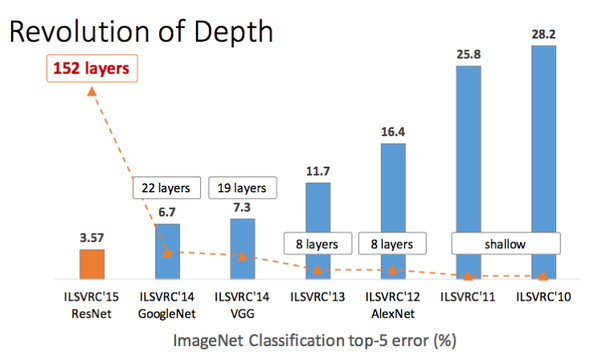
下圖為由史丹佛教授李飛飛所舉辦的影像辨識比賽之各年度冠軍錯誤率。以 [imagenet](http://www.image-net.org/) 作為資料集,縱軸為影像辨識之錯誤率,方匡中數字代表網路層數。隨著錯誤率的降低,網路的層數也越來越深。
:::
> imagenet 有超過一千四百萬張圖片,總共超過兩萬個類別。而人類辨識之錯誤率大概在 5% 左右,在 2015 年之後電腦在影像辨識方面正式超越人類
### 激活函數 (Activation Function)
激活函數最重要的工作就是以臨界值為分界來轉換輸出的函數。在先前的感知器當中,我們透過輸出是否大於零作為分界。若輸出大於 $0$ 則輸出 $1$,否則輸出 $0$,這樣的表現稱之為階梯函數如下圖。

但是這樣輸出僅限於 $0$ 與 $1$,在神經網路的世界傳送的是連續的實數,因此導入 `Sigmoid` 與 `ReLu`。
#### Sigmoid
$\sigma(x)=\dfrac{1}{1+e^{-x}}$
`Sigmoid` 與階梯函數的輸出都介於零到一之間。但最大的不同在於 `Sigmoid` 為連續平滑的線段,對於每個不同的輸入皆有對應不同的輸出,且若輸入越小,則輸出越小,反之。

程式碼如下:
```clike=
float sigmoid (float x) {
return 1 / ( 1 + pow(M_E, -x));
}
```
#### ReLU
$f(x)=max(0,x)$
`ReLu` (Rectified Linear Unit) 在近期神經網路被大量使用。相較於 Sigmoid , ReLu 具有計算簡單的優勢,並不像 Sigmoid 需要涉及指數運算,能夠大幅減少計算量。

程式碼如下:
```clike=
float relu(float x) {
union {
float f;
int32_t i;
} out = {.f = x};
out.i = out.i & ~(out.i >> 31);
return out.f;
}
```
:::success
神經網路中,激活函數具有必須為非線性函數之限制。所謂的線性函數,就是任何輸入與輸出成一定的倍數。例如: $h(x)=cx$,對於任何 x 的輸出,都會是 $c$ 的倍數。如此一來,線性函數對於神經元間的疊加會失去意義。執行 $y(x)=h(h(h(x)))$ 得到 $y(x)=c^3x$的結果,僅需透過一個非隱藏層做乘法即可。這樣的結果並不能獲得網路疊加所帶來的好處。
:::
#### Softmax
$y_k=\frac{e(a_k)}{\sum_{i=1}^{n}e(a_i)}$
以手寫數字辨識為例,輸出層共有十個神經元分別代表數字零到數字九,其工作就是計算出輸入影像所屬類別之機率。如下圖所示,一張手寫數字 `2` 的圖片作為一個輸入,將其中每個 pixel 數值轉換成一個向量,經過神經網路計算出屬於 `2` 的機率值為 `0.7` ,既然為機率,所有輸出之各類別機率值相加為 `1`。
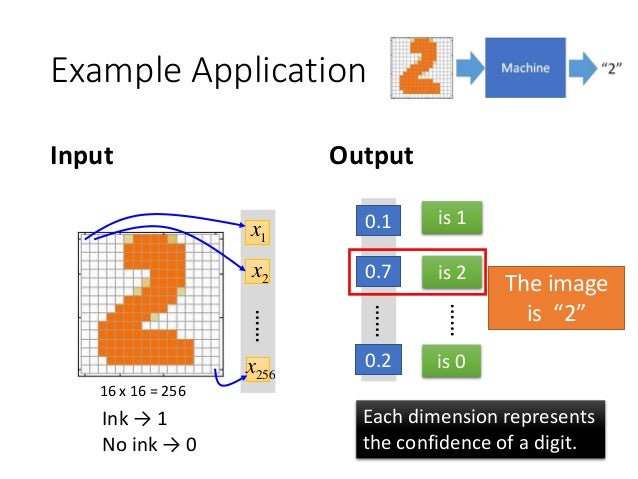
###### 圖片來源:[Tutorial for General Deep Learning Technology](https://speech.ee.ntu.edu.tw/~tlkagk/slide/Tutorial_HYLee_Deep.pdf)
程式碼如下,在 `line 13`中會減去input 中最大的數值來防範溢位,因為 softmax 在計算 $e^{a_k}$ 次方時可能會產生龐大的數值導致運算出錯:
```clike=
void softmax(float *x) {
int i = 0;
float x_max = 0; // Find the max value in array to avoid overflow
float sum = 0;
/* Find the max value in the array */
for (i=0; i<SIZE; i++) {
x_max = max(x_max, x[i]);
}
/* Calculate the e^x and the sum value */
for (i=0; i<SIZE; i++) {
x[i] -= x_max;
x[i] = pow(M_E, x[i]);
sum += x[i];
}
/* The softmax output */
for (i=0; i<SIZE; i++) {
x[i] /= sum;
}
}
```
### 神經網路傳輸
在神經網路中,每個輸入、各個神經元之權重及偏權值都可以視為向量。因此每層的計算皆可以視為矩陣運算,透過輸入與權重相乘加上偏權值後,經過激勵函數輸出一向量後,便可傳遞給下一層直到到達輸出層。
* input:
$X=\left(
\begin{array}{c}
x_1 \\
x_2 \\
\end{array}
\right)$
* weight:
$W=\left(
\begin{array}{ccc}
w_{11} & w_{21} & w_{31} \\
w_{12} & w_{22} & w_{32} \\
\end{array}
\right)$
* bias:
$B=\left(
\begin{array}{c}
b_1 \\
b_2 \\
b_3 \\
\end{array}
\right)$
* output:
$\begin{align}
A=\sigma(x^TW+B)=\sigma(\left(
\begin{array}{c}
x_1 \\
x_2 \\
\end{array}
\right)^T
\left(
\begin{array}{ccc}
w_{11} & w_{21} & w_{31} \\
w_{12} & w_{22} & w_{32} \\
\end{array}
\right) +
\left(
\begin{array}{c}
b_1 \\
b_2 \\
b_3 \\
\end{array}
\right))=\left(
\begin{array}{c}
a_1 \\
a_2 \\
a_3 \\
\end{array}
\right)
\end{align}$

---
## Step 1 - 挑選一個神經網路
神經網路能由層與層的疊加得出,其中各層中具不同數量的神經元,組成各式組合的神經網路架構。因此在做深度學習的第一步,就是透過人類的智慧訂定一個神經網路的架構,在這個架構中選出一組參數(權重、偏權值),接著評估這組參數的好壞。
---
## Step 2 - 評估模型好壞
### 損失函數 (loss function)
在我們選定一組參數後,即可利用這組參數計算出對應的結果。如何評估模型的好壞,就是以損失函數作為一個指標。損失函數所代表的就是輸出與真實答案的誤差,若誤差越小,則這組參數就是一組好的參數,能夠越接近我們預期的結果;反之若損失函數越大,則在這組參數就不是一組好的參數。
#### 均方誤差 (Mean Square Error)
$E=\frac{1}{2}\sum_{k}(y_k-t_k)^2$
均方誤差很直覺的就是透過每個神經元輸出與正確答案相減取平方後再除以二。以手寫數字辨識為例 `y` 為神經元之輸出, `t` 為正確答案。在 `y_1` 中損失較小,對於神經網路來說 `y_1` 中的參數較好:
```
正確答案為 5 , 計算結果為 5 之機率最高
y_1 = [0.01, 0.03, 0.0, 0.05, 0.01, 0.7, 0.1, 0.1, 0.0, 0.0]
t = [0, 0, 0, 0, 0, 1, 0, 0, 0, 0]
mean_square_error = 0.056800
正確答案為 5 , 計算結果為 6 之機率最高
y_2 = [0.01, 0.03, 0.0, 0.05, 0.01, 0.1, 0.7, 0.1, 0.0, 0.0]
t = [0, 0, 0, 0, 0, 1, 0, 0, 0, 0]
mean_square_error = 0.656800
```
#### 交叉熵誤差 (Cross Entropy Error)
$E=-\sum_{k}t_klogy_k$
以手寫數字辨識為例 `y` 為神經元之輸出, `t` 為正確答案。$log$ 函數具有輸入越接近 `1` 時,輸出則越接近 `0` 。以輸出層之值作為輸入,當輸入越接近正確答案時,機率值越大, loss 越小;反之。
## Step 3 - 挑選最好的一組參數
我們可以透過 `loss` 這個指標,輸入為在神經網路計算的函數 $f$,目標就是找到一組 $w^*$ 及 $b^*$ 使得 `loss` 最小。
$f^*={\arg\min}_{f}L(f)$
$\begin{split}
w^*,b^*&=argmin_{w,b}L(w,b) \\
&= argmin_{w,b}\sum(\hat{y}-(b+wx_n))^2
\end{split}$
### 梯度
如何找到一組最好的參數呢,神經網路中參數個數可能成千上萬,不能像感知器一樣自行決定,因此我們導入梯度下降的概念,讓神經網路自動更新參數,也就是自己學習。
對於一個權重 $w$ ,觀察 $w$ 的走向使得 `loss`,最小,這就是梯度下降法的精神。其中最大的限制就是 $f$ 要可微分。
以下圖為例:
* 微分值為負 -> `loss` 走勢往下 -> 增加 $w$
* 微分值為正 -> `loss` 走勢往上 -> 減少 $w$
每次要更新多少,由兩個數值決定:
* 微分大小: $\frac{dL}{dw}|_{w=w^0}$
* 學習率 (Learning Rate): $\eta$
* 學習率是一種超參數,為一個是先訂定好的數值,可以決定每一步的大小。而也有像是 `Adagrad` 、 `Momemtum` 等方法能夠在執行時期自動決定學習率大小。
根據前面的 $w$ 、 $b$ 不斷更新
$w^1\leftarrow w^0-\eta\frac{dL}{dw}|_{w=w^0}$
$w^2\leftarrow w^1-\eta\frac{dL}{dw}|_{w=w^0}$
...
$b^1\leftarrow b^0-\eta\frac{dL}{db}|_{b=b^0}$
$b^2\leftarrow b^1-\eta\frac{dL}{db}|_{b=b^0}$
...
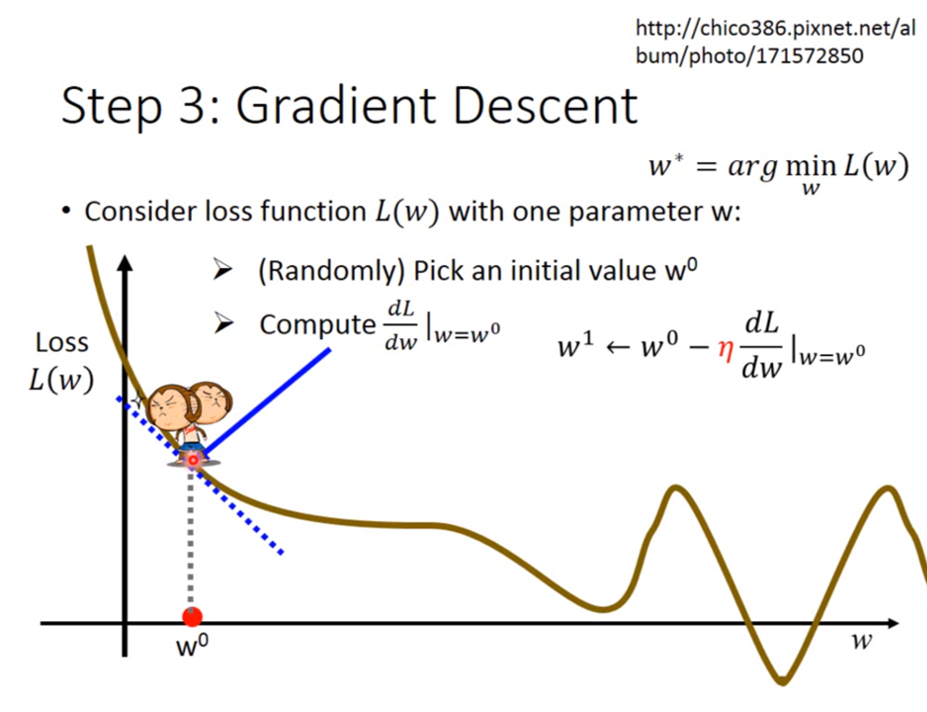
###### 圖片來源:[Tutorial for General Deep Learning Technology](https://speech.ee.ntu.edu.tw/~tlkagk/slide/Tutorial_HYLee_Deep.pdf)
### 反向傳播
#### chain rule
---
## 利用 C 語言實作兩層神經網路
### Dataset - MNIST
在這個資料集中,每張圖片都是固定大小 28*28 pixel 的圖片,每張圖片內容為一個手寫的數字

* 訓練資料: 60000 筆
* 測試資料: 10000 筆
source: [THE MNIST DATABASE of hand written digits](http://yann.lecun.com/exdb/mnist/)
### Network Structure
* 輸入層: 共有 28 * 28 共 784 個節點,其中 28*28 為資料集之圖片大小。主要功能為接收輸入。
* 隱藏層一: 以輸入層資料作為本層之輸出。共有 100 個節點,每個節點擁有 784 個權重 (與前一層輸入相同) 及一個偏權值。每個節點計算 $y=w_1x_1+w_2x_2+...+w_{784}x_{784}+b$ 之值,接著通過激勵函數後作為本層之輸出。
* 隱藏層二: 以上一層隱藏層輸出作為輸入。共有 10 個節點,每個節點擁有 100 個權重及一個偏權值。每個節點計算 $y=w_1x_1+w_2x_2+...+w_{100}x_{100}+b$ 之值。接著通過 softmax 作為輸出
* 輸出層: 輸出此次輸入之圖片所屬於哪個類別的機率值
### Implementation

```clike=
int main(void)
{
int batch_size = 100;
int iter_num = 1000;
// Load the mnist dataset
load_mnist();
init_INPUT_LAYER();
init_HIDDEN_LAYER();
for (i=0; i<iter_num;i++) {
/* Choose image randomly to train */
random_batch(batch_size);
/* Forward */
L1_forward(train_image, batch_size);
L2_forward(batch_size);
/* Calculate the loss of batch */
batch_cross_entropy(one_hot_train_label, batch_size);
/* Backward */
backward(train_image, one_hot_train_label, batch_size);
/* Update weight in each layer */
update_key(batch_size);
predict(train_image, one_hot_train_label, batch_size);
}
test();
return 0;
}
```
### Result
```
precision:86%
*******
***** ***
**** **
**** **
** **
** **
** **
** **
*** ***
*** ***
** ***
*** **
****
****
******
*** **
*** ***
*** **
*** ***
******
predict:8 answer:8
```
## 參考資料
* [YouTube Channel teaching Deep Learning and Machine Learning](https://www.youtube.com/channel/UC2ggjtuuWvxrHHHiaDH1dlQ/playlists)
* [deep-learning-from-scratch
](https://github.com/oreilly-japan/deep-learning-from-scratch)
---
## [CMSIS-NN: Efficient Neural Network Kernels for Arm Cortex-M CPUs](https://arxiv.org/pdf/1801.06601.pdf) 論文底下的 ReLU
* ReLU function
型式為:$f(x)=max(0,x)$,當 x 小於 0 的時候值為 0 ,當 x 大於 0 的時候它是斜率為 1 的線性函式
* 使用 SWAR(SIMD with a register) 改進
本篇 paper 的 register 大小為 8 bit ,為了要加速運算所以將 4 個 8 bit 的 register combine 在一起,變成一個 32 bit 的資料,接著用 bitwise 的方式將這 4 個 8 bit register 的值做修改
* 流程圖

* 虛擬碼
```c=
inA = *__SIMD32(pIn)++
buf = __ROR(in & 0x80808080,7)
mask = __QSUB(0X00000000,buf)
*__SIMD32(pOut)++ = inA & (~mask)
```
* 一開始會先讀進四個相鄰陣列的值
* 接著使用 _ROR 指令將 signbit 由高位轉到低位,將這個結果存到 buf,所以如果 register 值為正數, buf 就會存 0 ,值為負數 buf 就會存 1
* 再用 0 去減 buf 出來的值就會是我們的 mask,所以負數得到的 mask 為 `0xffffffff`,正數得到的 mask 為 `0x00000000`
* 將 mask 的值取反位元,在跟原來的值做 mask 這樣我們就會讓 register 是負的值變成 0 ,正的值維持不變
## 利用 SSE 指令實作 paper 的 ReLU
* SSE 介紹
intel x86 cpu 的架構中有 8 個 128 bit 的 register 為
XMM0~XMM7

,透過 SSE 提供的指令集我們可以利用這些 register 進行運算,實現 SIMD
* code
```c=
int a[] = {-2, 0, 1, 2};
__m128i inA = _mm_loadu_si128 ((__m128i const *)a);
__m128i mask = _mm_srai_epi32 (inA, 31);
inA = _mm_andnot_si128 (mask, inA);
_mm_storeu_si128 ((__m128i *) a, inA);
```
* function 講解
:::info
__m128i _mm_loadu_si128 (__m128i const* mem_addr)
:::
load 128 bit 的資料到 XMM0~XMM7 其中一個 register,然而大部分存取記憶體的 SSE 指令,都要求資料位址是 alignment 16 byte ,如果非 alignment 則會發生不可預期的錯誤。而這個 function 為 load==u==,u 為 unalignment 的縮寫代表即使 load 的資料並非 alignment 一樣可以運作。然而如果你知道你的 data 確切是 alignment 16 byte,則用 load 就好,畢竟 load 只要 1個讀取 cycle 就能處理完,而 loadu 還要先經過處理才能開始讀取。
:::warning
[What is the difference between loadu and load?](https://stackoverflow.com/questions/15964367/what-is-the-difference-between-loadu-and-load) 提到現在大部分的 cpu 處理器速度很快所以用 loadu 指令在 alignment data 所損失的效能是很小的,所以建議不確定 data 是否 alignment 的話還是用 loadu 會比較好
:::
:::info
_mm_srai_epi32 (__m128i a, int imm8)
:::
srai 為 shift right arithmetic integer 的縮寫,可以得知這個指令就是對 register 做算術位移,而右移幾位則是看 imm8 值為多少,所以如果是正數則 singnbit 為 0, 在右移 31 bit 後得到的值就為 `0x00000000` 反之負數值在右移 31 bit 後得到的值則為 `0xffffffff`,同時對 4 個整數做操作得到的值回傳為我們的 mask。
:::info
_mm_andnot_si128 (__m128i a, __m128i b)
:::
andnot 的操作為 `dst[127:0] := ((NOT a[127:0]) AND b[127:0])`,而我將 mask 取 not 之後,在跟原本的數值做 and ,則正數的 not mask 為 0xffffffff 所以 and 完保持不變,但是負數的 not mask 為 0x00000000 所以 and 完則變成 0,至此我們完成了用 SIMD 實作 ReLU function,但是還要再把結果從 register 存回 memory
:::info
void _mm_storeu_si128 (__m128i* mem_addr, __m128i a)
:::
將 a register 的值存回 memory ,然而跟 load 一樣這種存取記憶體的操作都有 alignment 的要求,所以我們在不確定資料是否 alignment 的情況下使用 storeu 而不是 store,來將我們的資料存回 a 矩陣
#…# 實驗
首先為了要比較我們寫的 SSE 版本的 ReLU 跟一般的 ReLU 的效能差異,我們寫了一個 bitwise 版的 ReLU 對只有 4 個元素的 矩陣做運算,並計算它跑 `100000000` 次的時間
* bitwise 版
```c=
double t1, t2;
int mask;
int a[] = {-2, 0, 1, 2};
t1 = tvgetf();
for (int j = 0; j < 100000000; j++)
{
for (int i = 0; i < 4; i++)
{
mask = a[i] >> 31;
a[i] = a[i] & ~(mask);
}
}
t2 = tvgetf();
```
跑完時間 `1.113199s`
* SSE 版本
一樣跑 100000000 次,但是時間為 `1.474672s`
## 討論實驗結果
:::info
為何使用了 SSE 反而跑得時間增多了?
:::
使用 perf 去觀測 cache miss 發現
* bitwise 版的 perf
```
Performance counter stats for './bitwiserelu':
25,666 cache-misses # 21.461 % of all cache refs
119,596 cache-references
7,502,546,330 instructions # 2.14 insn per cycle
3,512,418,744 cycles
1.119304823 seconds time elapsed
```
* sserelu 版的 perf
```
Performance counter stats for './sserelu':
28,085 cache-misses # 19.068 % of all cache refs
147,288 cache-references
3,103,093,304 instructions # 0.66 insn per cycle
4,667,694,489 cycles
1.484877411 seconds time elapsed
```
## 參考資料
* [Intrinsics Guide](https://software.intel.com/sites/landingpage/IntrinsicsGuide/)
* [sse 介紹](https://www.csie.ntu.edu.tw/~r89004/hive/sse/page_1.html)
* [What is the difference between loadu and load?](https://stackoverflow.com/questions/15964367/what-is-the-difference-between-loadu-and-load)
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet