<style>
#doc {
text-align: justify;
}
</style>
# 🔐 **zkPrivacy = Comparación entre ZKP - MPC & FHE**
> *Tu vida digital ya no es un libro abierto (ni para los algoritmos).*
Imagina despertar y empezar tu día sin preocupaciones mientras, tres cosas ocurren en segundo plano:
- Tu banco verifica que ganas lo suficiente para un préstamo... **sin conocer tu salario.**
- Un hospital en tu cuidad usa tus datos genéticos para investigar una cura... **sin acceder a tu ADN.**
- Un DAO vota tu propuesta de negocio... **sin descubrir que eres el dueño de la wallet que financia la competencia.**
Suena a utopía, pero ya está pasando.
La privacidad en el mundo digital ha experimentado una transformación radical en los últimos años. Desde el despegue de las Pruebas de Conocimiento Cero (ZKPs) en blockchain en 2022, el panorama tecnológico se ha diversificado considerablemente.
## Tres tecnologías transformadoras
Aunque no son descubrimientos nuevos, los recientes avances en criptografía avanzada han permitido implementar:
- **ZKPs (Pruebas de Conocimiento Cero)**: Utilizadas por proyectos como **Aleo y Aztec** para llevar privacidad a los contratos inteligentes.
- **MPC (Computación Multi-Partido)**: Implementada por **Fireblocks** y **Qredo**, revoluciona el procesamiento de datos sensibles en colaboración permitiendo que instituciones como bancos colaboren sin compartir toda su información.
- **FHE (Encriptación Totalmente Homomórfica)**: Desarrollada por startups como **Sunscreen** y **Fhenix**, permite operar con datos que permanecen cifrados durante todo el proceso, transformando los fundamentos del cómputo privado.
### Un nuevo estándar
Esta convergencia crea un nuevo lenguaje de confianza digital y redefine la privacidad. Estas tecnologías no solo mejoran la seguridad en Web3, sino que establecen bases para aplicaciones donde la privacidad es fundamental. En este paradigma, la protección de datos no es opcional sino el principio sobre el que se construye toda la arquitectura. Las empresas que adopten este enfoque ofrecerán soluciones que respeten la información sensible mientras mantienen la funcionalidad necesaria.
## **¿Qué es FHE?**
La Encriptación Totalmente Homomórfica (FHE) es una tecnología de privacidad que utiliza **propiedades homomórficas** matemáticas para realizar diversos cálculos sobre datos cifrados. Durante todo el proceso u operación, los datos permanecen seguros y privados. En pocas palabras, FHE permite procesar datos sin descifrarlos o revelar información. Comúnmente se usa para cifrado de información médica, privacidad de datos financieros y cifrado de datos en la nube.
**Las propiedades homomórficas** permiten operar con datos encriptados, sin desencriptar. Al final, el resultado desencriptado es igual al de operar con los datos reales. Más adelante lo explicaremos en detalle.


FHE permite un número ilimitado de cálculos y operaciones con los datos cifrados, la cual es la principal diferencia respecto a otras formas Encriptación Homomorfica (HE), como el Cifrado Parcialmente Homomórfico (PHE) y el Cifrado Algo Homomórfico (SHE). Aunque ofrece la máxima flexibilidad, es computacionalmente costoso y, por lo tanto, menos práctico para algunos usos.
- **Las tres principales categorías de encriptación homomórfica son:**
- **PHE (Cifrado Parcialmente Homomórfico):**
Solo permite una operación (por ejemplo, solo sumas o solo multiplicaciones).
- **SHE (Somewhat HE):** Permite varias operaciones, pero limitadas antes de que el ruido sea demasiado.
- **FHE (Cifrado Totalmente Homomórfico):**
Permite operaciones ilimitadas sobre los datos cifrados.
## **Comprendiendo fundamentos matemáticos de FHE**
La idea central de la FHE es sencilla: al permitir operaciones directas sobre textos cifrados, la FHE habilita el procesamiento seguro y privado de información sensible sin exponer jamás los datos originales en claro.
Uno de los pilares matemáticos del Cifrado Homomórfico Total (FHE) son los **mapas multilineales.** Estas funciones permiten operaciones seguras y eficientes sobre datos cifrados, pero su concepto puede resultar abstracto. Aquí lo desglosamos:
**¿Qué son los mapas multilineales?**
En matemáticas, un mapa multilineal es una función que toma múltiples entradas (de espacios vectoriales o grupos algebraicos) y genera una salida, manteniendo la linealidad en cada variable por separado. Por ejemplo:
- Un mapa bilineal (2-lineal) satisface:
$$
e(a \cdot \vec{v}, \vec{w}) = a \cdot e(\vec{v}, \vec{w}) \; \; y \; \; e(\vec{v} + \vec{v^{\prime}}, \vec{w}) = e(\vec{v}, \vec{w}) + e(\vec{v^{\prime}}, \vec{w})
$$
En criptografía, se usan para construir operaciones complejas que preservan propiedades algebraicas sin revelar información sensible.
**Relación con el FHE**
En FHE, los mapas multilineales son clave para:
- **Habilitar operaciones profundas:** Permiten componer múltiples operaciones (sumas, multiplicaciones) sobre datos cifrados, controlando el ruido generado.
- **Garantizar seguridad:** Se basan en problemas computacionalmente difíciles, como el Problema Multilineal de Decisión de Diffie-Hellman (MDDH), que protege contra ataques incluso con acceso a cálculos intermedios.
- **Construir esquemas eficientes:** Esquemas como BGV, BFV o CKKS usan variantes de mapas multilineales (e.g., encodings graduales) para optimizar operaciones.
**Resumen**
Los **mapas multilineales** son la magia oculta detrás del FHE:
- Convierten problemas criptográficos difíciles en operaciones viables sobre datos cifrados.
- Varían en implementación según el esquema, pero todos aprovechan sus propiedades para balancear seguridad, eficiencia y funcionalidad.
- Su evolución sigue siendo crítica para lograr FHE más rápido y accesible.
En FHE, se debe añadir **ruido aleatorio** a los **datos cifrados** para garantizar la seguridad, pero también significa que todos los cálculos se realizan no solo sobre los datos cifrados, sino también sobre el ruido añadido. El **ruido aleatorio** es como un "desorden controlado" que se añade al dato cifrado para hacerlo más difícil de adivinar. Esto lo hace más resistente a los ataques que intentan descifrar el contenido. Este ruido protege el secreto.
***`Texto cifrado = datos cifrados + ruidos`***

**Problema: el ruido crece con cada operación**
Si el ruido crece demasiado, sobrescribirá bits de datos con otros aleatorios.

A continuación se ejemplificara este problema del crecimiento del ruido:
Se presenta el siguiente escenario
1. **Texto Plano (Datos Originales):**
El dato original es un polinomio (expresiones con términos como 3x⁵ + x⁴ + 2x³ + ...) que trabajan bajo dos reglas:
* **Módulo xⁿ + 1:** Los polinomios "se doblan" para que no crezcan demasiado, es decir, controla el "tamaño" de los coeficientes. (x⁵, x⁴, etc.).
```
¿A qué nos referimos con el término "doblar"?
Piensa en un reloj de 12 horas (mod 12), podrías: Si son las 15:00 pm, el reloj "dobla" las horas y muestra 3:00 am (porque 15 − 12 = 3).
Aquí xⁿ + 1 es como el "reloj" que reinicia los términos del polinomio.
```
* **Módulo p:** Los coeficientes (números como 3, 1, 2) se reducen para mantenerlos pequeños. Controla el "tamaño" de los coeficientes (3, 100, −5, etc.).
```
Imagina que solo puedes usar números del 0 al 4 (como si tuvieras una calculadora que solo muestra 1 dígito). Cada vez que un número pasa de 4, "da la vuelta" (como un odómetro de coche):
5 se convierte en 0,
6 en 1,
y así sucesivamente.
Así, los números nunca se salen de control.
```
Ejemplo: 3x⁵ + x⁴ + 2x³ (datos originales antes de cifrar).
Ambos trabajan juntos para que los polinomios sean manejables y seguros en criptografía.
2. **Texto Cifrado (Datos Protegidos):**
También son polinomios, pero con dos diferencias clave:
* **Módulo xⁿ + 1:** Igual que antes (para mantener la estructura).
* **Módulo q**: Ahora los coeficientes son números mucho más grandes (ej. 7862x⁵ + 5652x⁴ + ...), lo que los hace parecer aleatorios y seguros.
### Diferencia clave: p vs q
| Característica | Módulo `p` (Texto Plano) | Módulo `q` (Texto Cifrado) |
|----------------------|-----------------------------------|-----------------------------------|
| **Tamaño típico** | Pequeño (ej: 5, 17) | Grande (ej: 32,768) |
| **Coeficientes** | Números simples (3, -1, 2) | Números grandes (7862, -45293) |
| **Propósito** | Mantener eficiencia computacional | Garantizar seguridad criptográfica|
| **Operaciones** | Aritmética exacta | Aritmética con "ruido" controlado |
| **Visibilidad** | Datos legibles | Apariencia aleatoria |
| **Relación con LWE** | No aplica | Base para añadir ruido seguro |
**¿Por qué esto es seguro?**
Gracias al problema **Learning with Errors (LWE):**
* Al cifrar, se añade "**ruido**" (errores pequeños pero aleatorios) a los coeficientes.
* Sin la clave secreta, el texto cifrado parece un polinomio caótico e inutilizable.
* Solo con la clave se puede eliminar el ruido y recuperar el polinomio original.
🔹 Ventaja: ¡Puedes sumar o multiplicar estos polinomios cifrados directamente! El resultado, al descifrarlo, coincidirá con las operaciones hechas en el texto plano.
El diagrama a continuación representa está encriptación sencilla, donde cada componente puede expresarse como un coeficiente en un polinomio o un vector. La altura del elemento representa el tamaño de los coeficientes. Nota que en el primer paso, el ruido inicial es pequeño.

A medida que aumenta el número de cálculos (operaciones), vemos un crecimiento correspondiente en el ruido. El crecimiento en el ruido puede describirse como exponencial, polinómico, lineal, constante o logarítmico.

A medida que aumenta el número de cálculos (operaciones), vemos un crecimiento correspondiente en el ruido. El crecimiento en el ruido puede describirse como exponencial, polinómico, lineal, constante o logarítmico.

**Solucion: Bootstrapping reduce el ruido**
Bootstrapping es una operación especial que restablece el ruido a su nivel nominal, permitiendo así más cálculos sin comprometer la integridad de los datos.
Para entender el bootstrapping, primero debemos comprender dos propiedades de un criptograma homomórfico: el **nivel** y el **ruido**. El **ruido** está asociado al criptograma sin importar el esquema subyacente (FHE incluye esquemas como BGV, BFV, CKKS y TFHE, que permiten calcular con datos cifrados sin descifrarlos). El **nivel**, en cambio, solo se aplica a los criptogramas de las familias BGV, BFV y CKKS. En la mayoría de estos esquemas, cada multiplicación homomórfica consume un nivel, lo que reduce el valor del nivel asociado al criptograma y aumenta el ruido.

Tras cierto número de operaciones (dependiendo del esquema), no se puede continuar. Esto ocurre porque se alcanza el nivel cero (por multiplicaciones sucesivas), el ruido crece demasiado (por muchas sumas) o, más comúnmente, ambas razones.
En este punto, aplicamos el **bootstrapping**. Esto restablece el nivel a un valor más alto y, según el esquema, puede reducir el ruido. El bootstrapping suele ser una operación costosa (aunque mejoras recientes lo han acelerado), por lo que generalmente se intenta evitar.
En la mayoría de aplicaciones, lo relevante es la baja latencia (evaluar una función rápidamente) más que el alto rendimiento.
**Resumen**
El bootstrapping permite continuar computaciones homomórficas indefinidamente, ajustando niveles y ruido. Su comportamiento y rendimiento dependen del esquema:

## **Conceptos Clave y Operaciones**
Comprender los conceptos clave y las operaciones de la criptografía homomórfica completamente (FHE) es esencial para aprovechar su potencial y utilizar sus capacidades de manera efectiva. Exploremos estos conceptos y operaciones.

#### 1. **Generación de claves**
Es el primer paso: se crea un par de claves (pública y privada) mediante algoritmos matemáticos seguros.
- La **clave pública** (`pk`) cifra los datos.
- La **clave privada** (`sk`) los descifra.
En esquemas FHE típicos, la generación de claves se expresa como:
$$
(\mathrm{sk}, \,\mathrm{pk}) \leftarrow \mathrm{KeyGen}(1^\lambda)
$$
Donde:
- $\lambda$ es el parámetro de seguridad
- $sk$ es la clave privada (secret key)
- $pk$ es la clave pública (public key)
La confidencialidad y aleatoriedad de la clave privada son críticas para la seguridad del sistema.
#### 2. Cifrado
Convierte un mensaje claro \(m\) en un texto cifrado \(c\) que soporta operaciones homomórficas:
$$
c \leftarrow \text{Encrypt}(pk,\,m)
$$
- $m$: mensaje original.
- $c$: texto cifrado.
- $pk$: clave pública.
El texto cifrado que contiene información adicional, lo que permite realizar operaciones directamente sobre él sin necesidad de descifrarlo.
**Dos características son esenciales:**
* **Corrección:** Garantiza que el texto cifrado pueda descifrarse correctamente con la clave privada.
* **Indistinguibilidad:** Hace que el texto cifrado aparezca ruido aleatorio, evitando que atacantes extraigan información.
Este proceso utiliza operaciones como aritmética modular o manipulación polinomial, adaptadas al marco criptográfico de la FHE.
#### 3. Circuito de evaluación
Define qué operaciones pueden realizarse sobre los textos cifrados. Por ejemplo, para una función \(f\) de \(n\) variables:
$$
c_{\text{res}} \leftarrow \mathrm{Evaluate}(\mathrm{pk},\,f,\,c_1,\,c_2,\,\dots,\,c_n)
$$
- $f$: función (suma, multiplicación, comparación, …).
- $c_1, c_2, ..., c_n$: textos cifrados de entrada.
- $c_{\text{res}}$: texto cifrado del resultado.
#### 4. Descifrado
Recupera el mensaje original \(m\) a partir de un texto cifrado \(c\) usando la clave privada:
$$
m \leftarrow \mathrm{Decrypt}(\mathrm{sk},\,c)
$$
- $c$: texto cifrado.
- $sk$: clave privada.
Debe ser exacto, pues cualquier error comprometería la integridad del resultado.
```mermaid
flowchart LR
subgraph "1. Generación"
keygen["KeyGen"] --> sk["Clave Privada"]
keygen --> pk["Clave Pública"]
end
subgraph "2. Cifrado"
m["Mensaje"] --> encrypt["Encrypt"]
pk --> encrypt
encrypt --> c["Texto cifrado"]
end
subgraph "3. Evaluación"
c --> eval["Evaluate"]
eval --> cres["Resultado cifrado"]
end
subgraph "4. Descifrado"
cres --> decrypt["Decrypt"]
sk --> decrypt
decrypt --> result["Resultado final"]
end
classDef gen fill:#e6f7ff,stroke:#0099cc
classDef enc fill:#e6ffe6,stroke:#009933
classDef eva fill:#fff2e6,stroke:#ff9933
classDef dec fill:#ffe6e6,stroke:#cc0000
class keygen,sk,pk gen
class m,encrypt,c enc
class eval,cres eva
class decrypt,result dec
```
---
### Homomorfismo
Es una función entre dos estructuras algebraicas (como grupos, anillos o espacios vectoriales) que **preserva la operación** de la estructura. En otras palabras, un homomorfismo mantiene la relación entre los elementos de las dos estructuras.
### Homomorfismos en Grupos
Sean \( (G, ∗) \) y \( (H, ⋅) \) dos grupos. Una función \( f: G → H \) se llama **homomorfismo** si, para todos los elementos \( a, b ∈ G \), se cumple que:
$$
f(a ∗ b) = f(a) ⋅ f(b)
$$
Esto significa que la operación en el grupo \( G \) se preserva a través de la función \( f \) al transformarse en la operación correspondiente en \( H \).
### Homomorfismos de Anillos
Para anillos, que tienen dos operaciones (suma y multiplicación), un homomorfismo \( f \) entre dos anillos \( (R, +, ⋅) \) y \( (S, ⊕, ⊗) \) debe cumplir:
- **Preservación de la suma:**
$$
f(a + b) = f(a) ⊕ f(b)
$$
- **Preservación de la multiplicación:**
$$
f(a ⋅ b) = f(a) ⊗ f(b)
$$
Gracias a esta propiedad, se pueden realizar **cálculos en el espacio del texto plano (plaintext)** y reflejar automáticamente esos resultados en el **espacio cifrado (ciphertext)** mediante el cifrado homomórfico.
---
#### Ejemplo con el Cifrado RSA
Este diagrama ilustra visualmente cómo funciona la propiedad homomórfica multiplicativa del RSA a través de dos caminos:
- **Camino 1**: Multiplica los mensajes originales y luego cifra el resultado.
- **Camino 2**: Cifra primero ambos mensajes y luego multiplica los mensajes cifrados.
El diagrama demuestra matemáticamente que ambos caminos llegan al mismo resultado final, permitiendo realizar cálculos sobre datos cifrados sin necesidad de descifrarlos primero.
```mermaid
flowchart LR
subgraph "Camino 1: Multiplicación y luego cifrado"
m1(["Mensaje m₁"]) --> mul["×"]
m2(["Mensaje m₂"]) --> mul
mul --> prod["m₁·m₂"]
prod --> cifProd["Cifrado\nE(m₁·m₂) = (m₁·m₂)ᵉ mod n"]
end
subgraph "Camino 2: Cifrado y luego multiplicación"
m1b(["Mensaje m₁"]) --> cifM1["Cifrado\nE(m₁) = m₁ᵉ mod n"]
m2b(["Mensaje m₂"]) --> cifM2["Cifrado\nE(m₂) = m₂ᵉ mod n"]
cifM1 --> mulCif["×"]
cifM2 --> mulCif
mulCif --> prodCif["E(m₁)·E(m₂) = m₁ᵉ·m₂ᵉ mod n\n= (m₁·m₂)ᵉ mod n"]
end
cifProd --> equal(("="))
prodCif --> equal
equal --> conclusion["Propiedad Homomórfica:\nE(m₁)·E(m₂) = E(m₁·m₂)"]
classDef plaintext fill:#d4f1c5,stroke:#333
classDef ciphertext fill:#ffcccc,stroke:#333
classDef operation fill:#d4e6f1,stroke:#333
classDef result fill:#f9e79f,stroke:#333
classDef conclusion fill:#d7bde2,stroke:#333
class m1,m2,m1b,m2b plaintext
class cifM1,cifM2,cifProd,prodCif ciphertext
class mul,mulCif operation
class prod result
class conclusion conclusion
```
Este comportamiento es característico de los sistemas **homomórficos**, ya que nos permite realizar operaciones (en este caso, multiplicación) directamente sobre los datos cifrados sin necesidad de descifrarlos.
### Modelos de Cálculo Homomórfico
Para diseñar cálculos de Cifrado Homomórfico (HE), es importante elegir el enfoque adecuado según las características requeridas:
| Enfoque | Características | Esquemas Seleccionados |
| :--------------------------- | :---------------------------------------------------------------------------------------------------------------- | :------------------------------------ |
| **Circuitos Booleanos** | - Comparación rápida de números.<br>- Soporte para circuitos booleanos arbitrarios.<br>- Arranque rápido (refresco). | - GSW<br>- FHEW<br>- TFHE |
| **Aritmética Modular (Exacta)**| - Cálculos SIMD eficientes sobre vectores de enteros (usando batching).<br>- Aritmética de enteros de alta precisión.<br>- Multiplicación escalar rápida.<br>- Diseño por niveles (sin arranque). | - BV<br>- BGV<br>- BFV |
| **Aritmética de Números Aproximados**| - Aproximación polinómica rápida.<br>- Inverso multiplicativo y DFT relativamente rápidos.<br>- Cálculos aproximados profundos (ej. regresión logística).<br>- Cálculos SIMD eficientes sobre vectores reales (batching).<br>- Diseño por niveles (sin arranque). | - CKKS |
### Esquemas de Encriptación Homomórfica Completa (FHE)

- **BGV y BFV:** Los esquemas BGV (2011) y BFV (2012) mejoraron el rendimiento al introducir el concepto de Learning With Errors (LWE). BGV redujo el tiempo de operación de minutos a segundos, mientras que BFV utilizó anillos polinomiales (Ring-LWE) en lugar de ecuaciones lineales. Son adecuados para aplicaciones de recuperación de información y consultas de bases de datos.
- **TFHE:** La Encriptación Homomórfica Completa sobre el Torus (TFHE) (2016) mejoró el bootstrapping con una tabla de búsqueda, reduciendo los tiempos de segundos a milisegundos. Aunque originalmente solo soportaba circuitos booleanos, versiones como TFHErs permiten bootstrapping sobre enteros, siendo adecuada para cálculos generales.
- **CKKS:** CKKS (2016) es ideal para trabajar con números reales en problemas de aprendizaje automático, regresiones y cálculos estadísticos. Maneja aritmética aproximada, lo que lo hace menos adecuado para aplicaciones que requieren precisión financiera.
## **Beneficios de FHE**
- **Seguridad en el Procesamiento:** Los datos cifrados, no necesitan ser convertidos a texto plano antes de que se puedan realizar cálculos. Esto mantiene la información protegida durante todo el proceso de computación.
- **Alta Resistencia a Ataques:** Requiere un esfuerzo computacional extremadamente alto para descifrar datos que han sido cifrados con FHE. Esta característica hace que sea prácticamente imposible comprometer la seguridad de los datos incluso con recursos significativos.
- **Cifrado Permanente:** Los datos cifrados permanecen cifrados en todo momento, independientemente de los procesos que necesiten realizarse sobre los datos.
## **Limitaciones de FHE**
- **Alto Consumo de Recursos:** Requiere una inversión de hardware y capacidad de procesamiento para procesar datos cifrados durante todo el proceso.
- **Complejidad Técnica:** Requiere un nivel alto de experiencia técnica y conocimiento especializado.
- **Rendimiento Limitado:** Para alcanzar velocidades aceptables, se necesitan múltiples optimizaciones y ajustes técnicos, lo que aumenta aún más su complejidad.
- **Adopción Limitada:** Adopción en entornos de producción está limitada por problemas de rendimiento y precisión.
La clave para lograr vencer estas ‘limitaciones’ que implican una velocidad de procesamiento y problemas de precisión sobre todo para escenario o aplicaciones que necesiten cálculos intensivos con una gran cantidad de datos, la solución para FHE radica en la aceleración por hardware y madurez en desarrollo.
## **Recapitulación de FHE**
FHE tiene tres características principales: homomorfismo completo, confidencialidad de datos y flexibilidad computacional.
- **Homomorfismo Completo:** El Cifrado Totalmente Homomórfico (FHE) permite realizar cualquier operación matemática sobre datos cifrados, incluyendo suma, multiplicación e incluso operaciones compuestas más complejas, mientras que el resto de los esquemas de cifrado homomórfico solo admiten operaciones específicas.
- **Confidencialidad de datos**: Permite realizar múltiples sumas y multiplicaciones sobre datos cifrados, manteniendo el resultado cifrado.
- **Flexibilidad Computacional:** FHE admite una gama de operaciones computacionales, incluyendo suma, multiplicación y operaciones booleanas. Esta tecnología tiene ventajas de privacidad, pero aún hay margen de mejora para aplicaciones que requieren alta eficiencia en el procesamiento y cómputo de datos a gran escala.
## **Aplicaciónes de FHE en Blockchain**

## **Proyectos de FHE en Blockchain**

---
## **¿Qué es MPC?**

El **Cómputo Multipartito Seguro (MPC)** es un **protocolo criptográfico** que **permite a múltiples partes realizar cálculos sobre datos sin revelar su información entre sí.** En otras palabras (y de forma más sencilla), es un truco criptográfico que permite que personas u organizaciones trabajen juntas y obtengan resultados específicos, manteniendo la información de cada uno privada y segura.
Utiliza **cifrado** y **secret sharing** (compartición secreta) para garantizar la privacidad y seguridad durante el proceso de cómputo. En este enfoque, un dato se divide en "fragmentos" y se distribuye entre los participantes. La información sigue protegida porque ningún fragmento individual revela nada útil. Solo cuando se combinan suficientes fragmentos se puede reconstruir el dato original o proceder con el cálculo de forma segura.
Gracias a estas técnicas, MPC permite realizar cálculos manteniendo la privacidad, permitiendo a las partes colaborar en análisis de datos sin comprometer la confidencialidad de su información.
Cada protocolo válido de MPC debe cumplir dos requisitos específicos:
- **Privacidad en caso de comportamientos deshonestos:** Si los participantes revelan su información secreta o descartan las reglas durante el cálculo, el protocolo MPC no permitirá que los participantes deshonestos obliguen a las partes honestas a revelar su información confidencial ni influir en el resultado.
- **Imposibilidad de deducir los secretos:** Ningún participante puede deducir la información secreta de los demás a partir de la ejecución del protocolo. Esto significa que el resultado del cálculo no da ninguna pista sobre la información privada que cada participante posee.
## **Conceptos Clave y Operaciones**
Los protocolos MPC generalmente operan a través de los siguientes pasos:
1. **Distribución de entradas:** Cada participante divide su entrada en múltiples fragmentos y los distribuye entre todas las partes.
2. **Cómputo:** Las partes realizan cálculos sobre los fragmentos sin reconstruir los datos originales. Esto puede incluir operaciones aritméticas o funciones más complejas.
3. **Reconstrucción del resultado:** Tras completar el cálculo, los participantes combinan sus fragmentos para generar el resultado final, que puede verificarse públicamente sin revelar ninguna entrada privada.
## **Beneficios de MPC**
- **Terceros no tienen acceso a los datos:** Los datos no son vulnerables a terceros o inteligencia externa. MPC reduce la dependencia de proveedores externos al mantener los datos y cálculos seguros dentro de las redes internas de las organizaciones.
- **Preserva la usabilidad y privacidad:** MPC facilita cálculos colaborativos sin enmascarar variables. La confidencialidad se mantiene intacta sin sacrificar la precisión.
- **Alta precisión y exactitud:** Los resultados cumplen y superan los estándares de precisión exigidos por los clientes.
- **Resistente a la computación cuántica:** Los datos se cifran durante su uso al dividirse y distribuirse entre participantes (mediante "compartición de secretos"), lo que los protege contra ataques cuánticos.
## **Limitaciones de MPC**
- **Sobrecarga computacional:** Para garantizar la seguridad, se deben generar números aleatorios durante el cálculo . Esta generación requiere recursos computacionales adicionales, lo que puede ralentizar el proceso.
- **Altos costos de comunicación entre participantes:** La compartición de secretos implica comunicación constante entre todos los actores, aumentando los costos en comparación con el cálculo en texto plano.
- **Suposición previa de participantes maliciosos:** Para implementar MPC de forma segura, se debe predecir y asumir la proporción de actores maliciosos en el cálculo conjunto.
## **Comprendiendo fundamentos matemáticos**
**Two-party Computation Protocols vs Multi-party Computation Protocols**
Imagina que tú y tus amigos pertenecen a una empresa reconocida donde se les asigno un salario individual, y quieren saber el promedio de sueldos en su empresa, pero sin decir cuál es el suyo por temas de confindencialidad.
SMPC permite que un conjunto de **n** participantes, cada uno con datos privados (**d₁, d₂, …, dn**) :arrow_right: esto sería sus salarios indivuales, pueda calcular una función pública **F(d₁, d₂, …, dn)** :arrow_right: que sería el resultado promedio de salarios, sin que ninguno de los participantes pueda conocer la información de los demás.
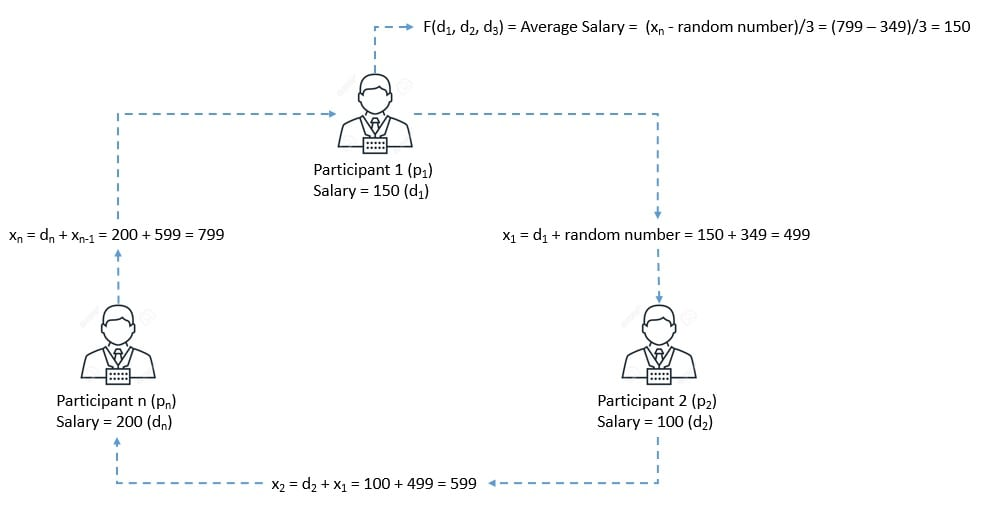
Es importante definir ciertos términos para enteder los fundamentos:
"*Ofuscar*" significa **ocultar o volver algo difícil de entender**, especialmente para proteger su significado original.
**Analogía útil:**
Imagina un examen de opción múltiple donde las respuestas no son **(A, B, C)**, sino **(X9#, P2$, K5&)**. Solo el profesor sabe qué letra corresponde a cada símbolo. Así funciona la ofuscación: esconde el significado, pero preserva la función.
**En seguridad:**
*Ofuscar no es cifrar* (que requiere una clave matemática), sino **enmascarar la estructura** para que, sin contexto, sea inútil.
Ahora bien el protocolo de MPC cambia significativamente **según el tipo** y **número de** tales **participantes en un sistema**:
## Two-party Computation Protocols
Los protocolos de computación segura **entre dos partes** permiten que dos entidades colaboren para calcular una función sin revelar sus entradas privadas. El **enfoque clave es** el uso de **circuitos garbleados**.
El **circuito garbleado** es un **protocolo criptográfico** que permite a **dos partes** calcular una función de manera segura sin revelar sus entradas privadas ni depender de un tercero de confianza. El proceso se basa en modelar la función como un circuito booleano, donde cada puerta lógica (como AND, OR, XOR) se ofuscan reemplazando sus entradas y salidas con etiquetas aleatorias (como códigos secretos), para que solo se pueda evaluar correctamente sin exponer información adicional. Así solo quien tiene las claves correctas puede "descifrar" la lógica oculta, evitando que un atacante entienda los datos reales.
**Componentes Clave**
* **Circuito Booleano:** Representa la función mediante puertas lógicas interconectadas, donde cada entrada y salida es un bit (0 o 1).

* **Transferencia Oblivious (OT):** Permite que una parte obtenga información específica sin que la otra sepa qué dato fue seleccionado. Esto es crucial para que el evaluador reciba las claves correctas sin revelar sus entradas.
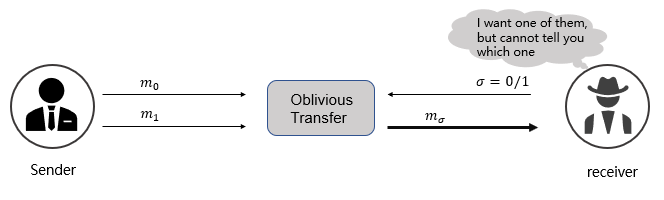
**Funcionamiento del Protocolo**

* **Generación del Circuito Garbleado (Garbler):**
1. Ofusca cada puerta asignando etiquetas aleatorias a las entradas y salidas.
2. Crea una tabla de cifrado donde solo la combinación correcta de etiquetas descifra el resultado válido.
* **Evaluación (Evaluator):**
1. Usa Transferencia Oblivious para obtener las etiquetas correspondientes a sus entradas.
2. Descifra selectivamente las puertas usando las etiquetas, propagando los resultados hasta obtener la salida final.
**Optimizaciones**
* **Point-and-Permute:** Reduce el esfuerzo de descifrado al usar bits de selección para identificar la fila correcta en cada puerta.
* **Free-XOR:** Permite calcular puertas XOR sin coste adicional, aprovechando relaciones predefinidas entre etiquetas.
* **Garbled Row Reduction (GRR):** Minimiza el tamaño de las tablas garbleadas eliminando filas redundantes.
* **Half Gates:** Reduce a solo dos cifrados por puerta AND, manteniendo compatibilidad con Free-XOR.
Estas técnicas permiten que el protocolo sea eficiente y seguro, ideal para aplicaciones como subastas privadas, comparaciones confidenciales o análisis de datos sin comprometer la privacidad.
<div style="display: flex; justify-content: center; border: 1px solid #ddd; width: 600px; height: 300px; overflow: hidden;">
<img
src="https://hackmd.io/_uploads/ByX7XO0ylg.png"
alt="Imagen con corte superior"
style="object-fit: cover; width: 100%; height: auto; margin-top: -40px;"
>
</div>
El concepto detrás de un protocolo de circuitos garbleados es sencillo pero poderoso. En esencia, el circuito garbleado actúa como una caja negra segura: ejecuta la lógica deseada, pero oculta todos los detalles internos.
Ahora se lo ejemplificará de forma sencilla.
Imagina dos partes, Alicia y Bruno, que quieren calcular una función sin revelar sus entradas privadas. Para lograrlo, usan un Circuito Garbleado, que funciona así:
1. **Representación de la Función**
Primero, la función que quieren calcular (que puede ser una fórmula matemática o código en un lenguaje de programación) se convierte en un **circuito booleano**.
2. **Garbling (Ofuscación del Circuito)**
Alicia (el "garbleador") encripta u ofusca el circuito. Pero a diferencia de un cifrado tradicional (que protege datos), aquí se encripta la función misma.
Cada puerta y entrada se reemplaza con etiquetas aleatorias (claves de evaluación), de modo que solo con las claves correctas se puede descifrar el resultado correcto.
3. **Evaluación del Circuito**
Mediante un protocolo llamado **Transferencia Oblivious (OT)**, Bruno obtiene las claves necesarias sin que Alicia sepa qué claves eligió.
Con estas claves, Bruno evalúa el circuito garbleado sin entender las entradas originales ni los valores intermedios.
Al final, solo el resultado de la función se revela, manteniendo todo lo demás en secreto.
## Multi-party Computation Protocols
Existen varias técnicas desarrolladas para la construcción de protocolos de computación multipartita segura, cada una con características diferentes. Algunas de las técnicas utilizadas en MPC son las siguientes:
1. **Shamir Secret Sharing:** es un método que divide un secreto (ej: una clave privada) en múltiples *shares* o "partes".
- **Notación**: `(t, n)`
- `n` = Total de partes generadas.
- `t` = Umbral mínimo para reconstruir el secreto.
> 💡 **Ejemplo**: En un esquema `(3, 4)`, se crean 4 partes y se necesitan al menos 3 para recuperar el secreto.
El siguiente diagrama ilustra el principio subyacente de un esquema de compartición de secretos {3,4}:

#### ¿Cómo funciona?
1. **Crear un Polinomio Secreto**
El *dealer* genera un polinomio aleatorio de grado `t-1`:
$$
f(x) = s + a_1x + a_2x^2 + \cdots + a_{t-1}x^{t-1}
$$
$$ s = Secreto \ ( \ valor \ en \ f(0)). $$
$$ a_1, a_2, ... = Coeficientes \ aleatorios.$$
2. **Generar las Partes (Shares)**
Cada participante $$ P_i \ \ recibe \ un \ punto \ \ ( \ i, f(i)). $$
> 💡 **Ejemplo**: para (3,4):
| Participante | Punto (x, y) |
|--------------|--------------|
| P1 (uno) | (1, f(1)) |
| P2 (dos) | (2, f(2)) |
| P3 (tres) | (3, f(3)) |
| P4 (cuatro) | (4, f(4)) |
3. **Reconstruir el Secreto**
Con al menos t puntos, usamos interpolación de Lagrange para hallar $$f(0) = s \ ( para \ conocer \ el \ secreto)$$
$$
s = \sum_{i=1}^{t} y_i \cdot \prod_{\substack{j=1 \\ j \neq i}}^{t} \frac{0 - x_j}{x_i - x_j}
$$
**Ejemplo Numérico (t=2, n=3)**
* Secreto: s = 7
* Polinomio: f(x) = 7 + 3x (grado 1)
Partes generadas:
$$
P1: (1, 10) → f(1) = 7 + 3*1 = 10
$$
$$
P2: (2, 13) → f(2) = 7 + 3*2 = 13
$$
$$
P3: (3, 16) → f(3) = 7 + 3*3 = 16
$$
Reconstrucción con P1 y P2:
$$
s = 10 \cdot \frac{0-2}{1-2} + 13 \cdot \frac{0-1}{2-1} = 10 \cdot 2 + 13 \cdot (-1) = 7
$$
Solo conociendo "cierta parte" del secreto, nos es posible reconstruir el polinonmio completo.
** ¿Por qué es seguro?**
* ❌ Con t-1 partes: Infinitos polinomios posibles → Imposible adivinar s.
* ✅ Con t partes: Solo un único polinomio posible → Secreto exacto.
> **Analogía**: Como un rompecabezas donde necesitas suficientes piezas para ver la imagen completa. 🧩
⚠️ Nota: En la práctica, los cálculos se realizan en un campo finito (ej: GF( p )) para evitar números no enteros.
Ahora vamos a recapitular para explicar ciertos conceptos técnicos:
**Compartición de Entradas**
Cada participante comparte su entrada utilizando el esquema de compartición de secretos de Shamir. El circuito se proporciona como entrada para el cálculo. Cada parte mantiene su entrada privada añadiendo un número aleatorio (masking), y al final, después de obtener el resultado, se elimina este valor aleatorio (conocido solo por esa parte), revelando el resultado correcto.
> Cada participante divide su secreto en partes. Todos juntas pueden reconstruirlo, pero individualmente no ven nada.
```mermaid
graph LR
A["$$ Entrada\ privada \ \ x_1$$"] -->|Divide| B(Share 1)
A -->|Shamir| C(Share 2)
A --> D(Share 3)
B --> E[Reconstrucción]
C --> E
D --> E
E --> F["$$Resultado \ \ f(x₁, x₂, x₃)$$" ]
```
**Evaluación del Circuito (Gate-by-Gate)**
El circuito se evalúa puerta por puerta, procesando las operaciones en secuencia desde las entradas hasta las salidas. Las operaciones básicas son suma y multiplicación sobre los shares distribuidos.
> Las operaciones se hacen por partes: sumas son fáciles (locales), multiplicaciones requieren colaboración.
```mermaid
flowchart LR
subgraph Circuito MPC
A["$$Share \ a_1$$"] --> Add["+"]
B["$$Share \ b_1$$"] --> Add
Add -->|"$$ \ \ a_1 \ + b_1$$"| C["$$Share \ c_1$$"]
A --> Mult["×"]
B --> Mult
Mult -->|"$$a_1 \ times \ b_1$$"| D["$$Share \ d_1$$"]
end
```
Ejemplo de cálculo para el participante $$i$$:
* Suma:
$$ c(i)=a(i)+b(i) \ ( \ local \ , sin \ comunicación). $$
* Multiplicación:
$$
c(i)=a(i)⋅b(i) \ ( \ requiere \ recombinación \ de \ shares).
$$
**Intersección de Conjuntos Privados (PSI)**
Protocolo eficiente para que dos partes encuentren elementos comunes en sus conjuntos sin revelar los elementos no compartidos. Útil incluso en entornos con adversarios maliciosos.
> Dos partes comparan sus datos cifrados. Solo descubren qué elementos tienen en común.
```mermaid
flowchart LR
P1["Parte 1<br>Conjunto A"] -->|"Encripta elementos"| PSI["PSI"]
P2["Parte 2<br>Conjunto B"] -->|"Encripta elementos"| PSI
PSI --> C["Comparación cifrada"]
C --> D["Resultado: A ∩ B"]
```
**MPC con Mayoría Honesta**
La función puede representarse mediante un circuito booleano o aritmético cuando hay mayoría honesta. En esquemas de compartición de secretos (MPC), se usa un campo finito
$$ Zp \ ( \ con \ p>n)
$$
para el circuito aritmético, el cual es **Turing completo.**
> Funciona cuando la mayoría es confiable. Los datos se dividen en partes y se procesan de forma segura entre todos.
```mermaid
flowchart TB
subgraph "Mayoría Honesta (t < n/2)"
A[Parte Honesta 1] -->|Shares| C[Circuito MPC]
B[Parte Honesta 2] -->|Shares| C
D[Parte Honesta 3] -->|Shares| C
C --> E[Resultado correcto]
end
```
Claves:
Seguro si los adversarios corruptos son minoría $$ (t<n/2).
$$
Usa aritmética modular en
$$ Zp $$
**MPC con Mayoría Deshonesta**
Cuando los adversarios pueden superar en número a los honestos, se requieren protocolos avanzados como:
* Transferencia Oblivious (GMW).
* Circuitos Cifrados (Yao).
* TinyOT (optimizado para eficiencia).
>Protege los datos incluso si hay más participantes maliciosos que honestos, usando técnicas avanzadas como circuitos cifrados.
```mermaid
flowchart LR
subgraph "⠀"
P1["Parte 1"] -->|"GMW/OT"| MPC["MPC"]
P2["Parte 2 (maliciosa)"] -->|"Garbled Circuits"| MPC
MPC --> R["Resultado seguro"]
end
```
Características:
* Resistencia a colusión: Seguridad incluso si la mayoría es corrupta.
* Overhead computacional: Más costoso que mayoría honesta.
**Criptografía Umbral**
Permite realizar operaciones criptográficas (ej: firmas) sin que ningún participante tenga la clave secreta completa. Basado en esquemas como RSA umbral:
$$y=x^e \ \ mod \ n
$$
(Donde x es el mensaje y e la clave pública).
>Nadie tiene la clave completa; se necesita un grupo mínimo para autorizar operaciones, evitando robos o fraudes.
```mermaid
flowchart TB
K[Clave Privada] -->|Dividida| P1[Share 1]
K --> P2[Share 2]
K --> P3[Share 3]
P1 & P2 --> F[Firma umbral]
F --> T[Transacción válida]
```
Beneficios:
* Tolerancia a fallos: Basta con un subconjunto de partes (ej: 3 de 5) para firmar.
* Seguridad distribuida: Ningún actor individual puede robar la clave.
### Comparativa: Mayoría Honesta vs. Deshonesta
| Criterio | Mayoría Honesta | Mayoría Deshonesta |
|----------------|-------------------------------------|--------------------------------------|
| **Seguridad** | Resistente a $t < n/2$ corruptos | Tolerancia a $t \geq n/2$ corruptos |
| **Protocolos típicos** | Shamir, BGW | GMW, Circuitos Cifrados |
| **Eficiencia** | Alta (menos overhead) | Baja (más pasos interactivos) |
| **Usos comunes** | Firmas umbrales, MPC básico | Mixnets, votaciones electrónicas |
## Recapitulacion de MPC
El **cómputo multipartito** es una técnica criptográfica que permite a varias partes, cada una en posesión de fragmentos de datos privados, participar en el cálculo de un resultado específico utilizando algoritmos basados en MPC. Este resultado específico se calcula combinando sus datos sin revelar la naturaleza ni el contenido de sus entradas, ni cualquier otra información secreta relacionada con el proceso.
En términos más simples, **MPC reúne entidades separadas que tienen piezas de información que, cuando se combinan, pueden revelar un secreto, firmar un mensaje o aprobar una transacción.** Es importante destacar que MPC logra esto sin revelar detalles sobre la información que posee cada individuo.
Es relevante mencionar que en MPC, los datos distribuidos entre múltiples participantes no representan el secreto si simplemente se combinan. En cambio, estos fragmentos de información sirven como entradas para participar en el cálculo deseado.
SMPC emplea **primitivas criptográficas** como:
- **Compartición secreta** (por ejemplo, Shamir’s Secret Sharing).
- **Cifrado homomórfico** (por ejemplo, Paillier, ElGamal).
- **Pruebas de conocimiento cero** (por ejemplo, zk-SNARKs, zk-STARKs).

---
## ¿Qué es Zero Knowledge?
Las pruebas de conocimiento cero (Zero-Knowledge Proofs o ZKP) representan uno de los avances más fascinantes en la criptografía moderna. Este método criptográfico permite a una persona (**el probador**) demostrar a otra (**el verificador**) que posee cierta información **sin revelar absolutamente nada sobre dicha información**, excepto el hecho de que la posee.

Concebidas originalmente en 1985 por Shafi Goldwasser, Silvio Micali y Charles Rackoff en su influyente publicación ["The Knowledge Complexity of Interactive Proof-Systems"](https://people.csail.mit.edu/silvio/Selected%20Scientific%20Papers/Proof%20Systems/The_Knowledge_Complexity_Of_Interactive_Proof_Systems.pdf), las ZKP establecen un sistema de prueba compuesto por tres elementos fundamentales: **el probador, el verificador y un desafío**. En esencia, resuelven una aparente paradoja: **¿cómo demostrar que conoces un secreto sin revelar el secreto mismo?**
### ¿Cómo funcionan las pruebas de conocimiento cero?
- #### **Los Tres Pilares Fundamentales**
Todo protocolo ZKP debe satisfacer tres criterios esenciales:
1. **Completitud**: Si dices la verdad y sigues las reglas, siempre convencerás al verificador. No hay falsos negativos en este juego.
2. **Solidez**: Es prácticamente imposible engañar al sistema. Un mentiroso será descubierto casi con total seguridad, convirtiendo la trampa en una apuesta perdida.
3. **Conocimiento cero**: El verificador termina el proceso exactamente como empezó: sin conocer nada nuevo excepto que el probador no miente.
- #### Los Protagonistas del Protocolo
Como en toda buena historia, tenemos personajes con roles bien definidos:
- **El Probador**: Posee el secreto y busca demostrarlo sin revelarlo.
- **El Verificador**: Cuestiona y examina para confirmar la verdad sin aprender el secreto.
- **La Declaración**: La afirmación que se intenta probar, desde conocer una contraseña hasta poseer una clave criptográfica.
```mermaid
sequenceDiagram
participant Emisor
participant Probador
participant Verificador
Emisor->>Probador: Emite datos secretos y públicos
Probador->>Verificador: Envía prueba
Verificador->>Probador: Verifica prueba
Verificador->>Verificador: Comprueba validez
Verificador->>Emisor: Confirma resultado de verificación
```
- #### Elemento básicos
En su forma más básica, tres movimientos elegantes:
- **El Testigo**: El secreto que el probador conoce. Este conocimiento le permite responder preguntas que solo alguien con esta información podría contestar correctamente.
- **El Desafío**: El verificador selecciona preguntas aleatorias que ponen a prueba el conocimiento del probador.
- **La Respuesta**: El probador contesta calculando la solución sin revelar el secreto subyacente. Cada respuesta correcta aumenta la confianza del verificador.
```mermaid
sequenceDiagram
participant Emisor
participant Probador
participant Verificador
Note over Emisor,Probador: El Testigo
Emisor->>Probador: Emite datos secretos y públicos
Note over Probador,Verificador: Compromiso
Probador->>Verificador: Envía prueba
Note over Verificador,Probador: El Desafío
Verificador->>Probador: Verifica prueba
Note over Verificador: Validación
Verificador->>Verificador: Comprueba validez
Note over Verificador,Emisor: La Respuesta
Verificador->>Emisor: Confirma resultado de verificación
```
La repetición de estos pasos reduce drásticamente la posibilidad de que alguien sin el conocimiento real pueda engañar al sistema por simple suerte. añadimos
## Comprendiendo fundamentos matemáticos de ZK
- #### NARK – Argumento No Interactivo de Conocimiento
Un **NARK** (Argumento no interactivo de conocimiento) es un tipo de prueba criptográfica en la que el probador demuestra a un verificador que conoce un testigo (un valor privado) que satisface una cierta afirmación (un circuito o una función computacional), sin revelar nada sobre ese testigo.
- **Modelo Computacional: Preprocesamiento**
1. **Circuito Aritmético (computación)**: Dado un circuito $C$, toma entradas públicas $x$ y entradas privadas $w$, y produce un valor en el campo $F$:
$$C(x, w) \rightarrow F$$
* $x$: entrada pública (pública para el verificador).
* $w$: entrada privada, también conocida como **testigo** o **witness** (privada para el probador).

- **Algoritmos**

1. **Algoritmo de Preprocesamiento $S$**: Dado un circuito $C$, el algoritmo de preprocesamiento genera parámetros públicos $pp$ y parámetros privados $vp$.
$$S(C) \rightarrow (pp, vp)$$
* $pp$: parámetros públicos, que estarán disponibles para el probador.
* $vp$: parámetros privados, que estarán disponibles para el verificador.
2. **Algoritmo del Probador $P$**: El probador genera la prueba, utilizando los parámetros públicos $pp$, las entradas públicas $x$ y el testigo privado $w$.
$$P(pp, x, w) \rightarrow \text{proof}$$
* La **prueba** es un conjunto de datos que demuestra que el probador sabe el testigo $w$ tal que $C(x, w) = 0$.
3. **Algoritmo del Verificador $V$**: El verificador toma los parámetros privados $vp$, las entradas públicas $x$ y la prueba generada por el probador, y verifica si la prueba es válida.
$$V(vp, x, \text{proof}) \rightarrow \text{aceptar} / \text{rechazar}$$
* Si la prueba es válida, el verificador acepta. Si no, la rechaza.
```mermaid
sequenceDiagram
participant Prep as "🔧 Preprocesamiento"
participant P as "👤 Probador"
participant V as "🔍 Verificador"
rect rgb(240, 255, 240)
Note over Prep: Algoritmo S convierte<br>el circuito C en parámetros
Note over Prep: S(C) → (pp, vp)
end
Prep->>+P: pp (parámetros públicos)
Prep->>+V: vp (parámetros privados)
rect rgb(255, 255, 240)
Note over P: Conoce el testigo privado w<br>⬇️
Note over P,V: Ambos conocen x (entrada pública)<br>⬇️
Note over P: Genera prueba usando<br>P(pp, x, w) → proof<br>⬇️
end
rect rgb(240, 248, 255)
Note over P,V: NARK: Protocolo no interactivo<br>(solo un mensaje de comunicación)
end
P->>V: Envía prueba (único mensaje)<br>➡️
rect rgb(255, 240, 245)
Note over V: Ejecuta algoritmo verificador<br>V(vp, x, proof)<br>⬇️
Note over V: Determina si Acepta o Rechaza<br>⬇️
end
```
* **Propiedades de un NARK:**
✅ **Completeness**
Si el probador conoce un testigo válido, el verificador siempre acepta:
$\Pr[V(vp, x, P(pp, x, w)) = \text{accept}] \approx 1$
✅ **Knowledge Soundness**
Si una prueba es aceptada, se garantiza que el probador conoce un testigo $w$ tal que $C(x, w) = 0$.
✅ **Zero-Knowledge (opcional)**
La prueba no revela ninguna información sobre el testigo $w$. Existen simuladores eficientes capaces de generar pruebas indistinguibles de las reales sin conocer $w$.
#### Snark
SNARK = S and NARK
- **Succinct**
* Tamaño de prueba: sublineal respecto al tamaño del testigo $w$
* Tiempo de prueba: sublineal respecto al tamaño del circuito $C$
- **Strongly Succinct**
* Tamaño de prueba: logarítmico en el tamaño del circuito $C$
* Tiempo de prueba: logarítmico en el tamaño del circuito $C$
- **Circuito**
* El verificador no tiene tiempo de leer el circuito
## Conceptos Clave y Operaciones
### zk-SNARKs
Los zk-SNARKs (SNARKs de conocimiento cero) permiten probar que conocemos variables **testigos** $w$ que satisfacen $F(x,w)=y$ para una función $F$ y una instancia pública $x$, sin revelar información sobre $w$.
### ¿Cómo se relaciona un zk-SNARK con un NARK?
* Un **SNARK** es un NARK que además es **sucinto**
* Un **zk-SNARK** es un SNARK que además es **zero-knowledge**
$\text{zk-SNARK} = \text{Succinct} + \text{Non-interactive} + \text{Argument of Knowledge} + \text{Zero-Knowledge}$
- ### Respecto al nombre:
* **Succinct**: las pruebas deben ser breves y rápidas de verificar. Esto permite delegar cálculos costosos a partes no confiables y verificar su validez sin ejecutar el programa uno mismo.
* **Non-interactive**: no requiere interacción entre probador y verificador, ni para generar ni para verificar la prueba. Se logra mediante la transformación de Fiat-Shamir.
* **Argument of Knowledge**: podemos probar con alta probabilidad que conocemos el testigo.
**Tipos principales:**
- Marlin (Aleo)
- PLONK
- STARKs
- Groth16
- Bulletproof
# Comparación Rápida de Algoritmos ZK proof
| Algoritmo | Prueba | Verificación | Setup | Post-Cuántico |
|:----------|:-------|:-------------|:------|:--------------|
| **Groth'16** | Excelente ~200B | Excelente ~1.5ms | Regular (Por circuito) | No |
| **PLONK/Marlin** | Bueno ~400B | Bueno ~3ms | Bueno (Universal) | No |
| **Bulletproofs** | Regular ~1.5KB | Débil ~3s | Excelente (Transparente) | No |
| **STARK** | Débil ~100KB | Regular ~10ms | Excelente (Transparente) | Sí |
## Resumen Visual
- **Mejor tamaño**: Groth'16 < PLONK < Bulletproofs < STARK
- **Más rápido**: Groth'16 < PLONK < STARK << Bulletproofs
- **Más confiable**: STARK = Bulletproofs > PLONK > Groth'16
- **Futuro seguro**: STARK > Todos los demás
### Elementos para contruir a Snark:
##### **Esquemas de Compromiso de Polinomios y Argumentos de Conocimiento**
- **Esquema de Compromiso de Polinomios
Permite obtener un argumento interactivo sucinto:**
- Se **compromete** (commit) un polinomio.
- Se **vincula** (bind) el compromiso al polinomio original.
- Luego se pueden **evaluar** los valores del polinomio sin revelarlo completamente.
- **Prueba de Oráculo Interactiva (IOP - Interactive Oracle Proof)**
- Se utiliza para verificar la **satisfacibilidad de circuitos** o sistemas R1CS.
- Permite **evaluar polinomios comprometidos** en uno o múltiples puntos, a lo largo de varias rondas.
- Extiende los compromisos de polinomios al modelo general de satisfacibilidad.
- **Heurística de Fiat-Shamir**
- Transforma una prueba **interactiva** en una prueba **no interactiva**.
- Sustituye los desafíos aleatorios del verificador por un hash determinista de la transcripción hasta ese punto.
```mermaid
graph LR
A["(1) Un esquema de compromiso funcional<br/>(objeto criptográfico)"] --> C(Transformación Fiat-Shamir);
B["(2) Una prueba de oráculo<br/>interactiva compatible (IOP)<br/>(objeto teórico de la información)"] --> C;
C --> D["SNARK para<br/>circuitos generales"];
style A fill:#f9f,stroke:#333,stroke-width:2px
style B fill:#f9f,stroke:#333,stroke-width:2px
style D fill:#ccf,stroke:#333,stroke-width:2px
```
**Construcción de SNARKs**
```mermaid
graph LR
subgraph "**Construcción de SNARKs"
direction LR
A[Construction] --> B;
A --> C;
subgraph "Polynomial IOP"
direction TB
B(Polynomial IOP) --> B1[Interactive proof:
- vSQL, Libra];
B --> B2[Multi-prover interactive proofs:
- Spartan];
B --> B3[Constant-round polynomial IOPs:
- Marlin, Plonk];
end
subgraph "Polynomial commitment"
direction TB
C(Polynomial commitment) --> C1[Pairing:
- KZG10];
C --> C2[Discrete logarithm:
- Bulletproof];
C --> C3[Hashing:
- FRI];
C --> C4[Groups of unknown order:
- DARK];
end
subgraph "Construction Details"
direction TB
A --> A1[Several polynomial IOP];
A --> A2[Several polynomial commitments];
A --> A3["Mixing up components:
- time (verification, proof)
- proof size
- setup assumptions
- post quantum"];
end
end
```
## Beneficios y Aplicaciones de las Pruebas de Conocimiento Cero
Las pruebas de conocimiento cero están redefiniendo el equilibrio entre verificación y privacidad, ofreciendo ventajas significativas en aplicación:
- ### Pagos anónimos
- Ocultan montos, remitentes y destinatarios en transacciones.
- Protegen la privacidad financiera frente a proveedores, bancos y autoridades.
- Habilitan “privacy coins” (Zcash) y servicios como Tornado Cash para transferencias completamente privadas.

- ### Protección de identidad
- Verifican atributos personales (ciudadanía, mayoría de edad) sin exponer datos sensibles.
- Facilitan la identidad descentralizada (“self-sovereign”) donde cada usuario controla qué se revela.
- Eliminan la necesidad de compartir pasaportes, números fiscales o documentos completos.

- ### Autenticación simplificada
- Permiten acceder a plataformas sin transmitir contraseñas ni almacenar grandes volúmenes de datos.
- Generan pruebas basadas en entradas públicas (pertenencia a un servicio) y privadas (credenciales del usuario).
- Mejoran la experiencia de usuario y reducen el riesgo de brechas de seguridad.

- ### Computación verificable (off-chain scaling)
- Externalizan la ejecución de cálculos a cadenas o servicios externos, reduciendo la carga en la red principal.
- Usan pruebas de validez para aplicar resultados sin re-ejecución, mejorando throughput y velocidad.
- Base de soluciones como ZK-rollups y validiums en Ethereum.

- ### Votación resistente a sobornos y colusión
- Garantizan votos anónimos, auditables y a prueba de censura.
- Impiden la identificación de preferencias individuales y la coordinación de sobornos.
- Mantienen la integridad electoral sin sacrificar privacidad.

### ZKP aplicaciones
| **Categoría** | **Beneficio Principal** | **Lo Más Destacado** | **Por Qué** |
|----------------------------------------|----------------------------------------------------------------|----------------------------------------|-------------------------------------------------------|
| **Blockchain – Identidad** | Verifica identidad sin exponer datos personales | Autenticación sin contraseñas | Protege la privacidad en accesos digitales |
| **Blockchain – Cadena de Suministro** | Valida orígenes y trazabilidad sin revelar secretos internos | Transparencia controlada | Cumple normativas y refuerza la confianza |
| **Blockchain – Interoperabilidad** | Facilita puentes seguros entre cadenas | Transferencias cross-chain privadas | Conecta ecosistemas sin exponer datos sensibles |
| **Blockchain – Almacenamiento** | Comprueba integridad de datos y cálculos off-chain | Almacenamiento cifrado verificable | Ideal para datos sensibles en redes descentralizadas |
| **Blockchain – Privacidad nativa (L1)**| Incorpora protección de datos desde el diseño de la cadena | Privacidad integrada | Seguridad garantizada sin capas adicionales |
| **Blockchain – Escalado (L2)** | Aumenta throughput y reduce costos | Rollups ZK y validiums | Descarga transacciones off-chain manteniendo validez |
| **Blockchain – Transacciones confidenciales** | Oculta montos y participantes | Confidential Transactions & Bulletproofs | Protege la información financiera en on-chain |
| **Blockchain – Prueba de Reservas** | Demuestra solvencia de exchanges sin revelar balances privados | Confianza pública | Evita fraudes y auditorías invasivas |
| **No-Blockchain – Verificación de atributos** | Comprueba propiedades (edad, solvencia…) sin exponer datos completos | Credenciales anónimas | Reduce la exposición de información personal |
| **No-Blockchain – Sistemas multiusuario** | Potencial privacidad y control granular en entornos compartidos | Interacciones seguras (MUI) | Protege datos de múltiples usuarios simultáneamente |
| **No-Blockchain – Votación electrónica** | Garantiza privacidad y auditabilidad de votos | Votos anónimos verificables | Refuerza la integridad electoral sin revelar preferencias |
| **No-Blockchain – ML confidencial** | Verifica inferencias y entrenamientos sin compartir datos | Modelos confiables | Crucial para sectores regulados (salud, finanzas) |
Si quiere saber mas en aplicaciones:
- [A Survey on the Applications of
Zero-Knowledge Proofs](https://arxiv.org/pdf/2408.00243v1)
## Desafíos y Limitaciones de las Pruebas de Conocimiento Cero
- ### Complejidad de Implementación
- Requieren conocimientos criptográficos avanzados, lo que dificulta su adopción por organizaciones sin experiencia especializada.
- ### Costos de Hardware
- Generar pruebas implica cálculos intensivos que exigen hardware especializado y costoso.
- ### Costos de Verificación
- La verificación también es exigente, aumentando los costos, especialmente en blockchains donde impacta en tarifas de gas.
- ### Configuración Confiable (en ZK-SNARKs)
- ZK-SNARKs dependen de una ceremonia inicial segura. Si se compromete, afecta la confianza y la seguridad.
- ZK-STARKs evitan este problema usando aleatoriedad pública.
- ### Sobrecarga de Rendimiento
- Las ZKPs pueden ralentizar los sistemas debido a su alta demanda computacional.
- ### Amenaza Cuántica
- ZK-SNARKs basados en curvas elípticas son vulnerables a computadoras cuánticas.
- ZK-STARKs ofrecen mayor resistencia.
## Recapitulición de ZKP
Las **Pruebas de Conocimiento Cero (ZKP)** demuestran posesión de información sin revelarla.
**Funcionamiento:** Interacción de desafío y respuesta para verificar el conocimiento del Testigo.
**Fundamentos:**
* **NARK:** Prueba no interactiva de conocimiento.
* **SNARK:** NARK sucinto (rápido y pequeño).
* **zk-SNARK:** SNARK con privacidad (cero conocimiento).
* **Tipos:** Groth'16, PLONK/Marlin, Bulletproofs, STARKs.
**Construcción (SNARKs):**
* Compromiso Polinomial.
* Prueba de Oráculo Interactiva (IOP).
* Heurística de Fiat-Shamir (para no interactividad).
**Beneficios:**
* Privacidad en transacciones e identidad.
* Autenticación eficiente.
* Escalado de computación.
* Votación segura.
* Aplicaciones en blockchain y fuera de ella.
**Desafíos:**
* Implementación compleja.
* Costos computacionales (prueba y verificación).
* Setup confiable (en algunos zk-SNARKs).
* Rendimiento.
* Resistencia cuántica (limitada en algunos tipos).
**ZK Landscape de los proyectos**

## **Recapitulación General y Comparación de ZKPs, MPC y FHE**
- **Pruebas de Conocimiento Cero (ZKPs):** Es un protocolo criptográfico donde un probador puede demostrar a un verificador que una declaración es verdadera, sin revelar ninguna información adicional más allá de la veracidad de la declaración. Esto se logra proporcionando una prueba de que la información cumple con cierta propiedad, sin revelar la información misma.
Una ejemplificación de ello es: Al solicitar un préstamo bancario, puedes demostrar que tu salario es suficiente sin mostrar tus estados de cuenta completos. El banco solo confirma que cumples el requisito sin ver tus movimientos.
- **Computación Multi-Parte (MPC):** Esta tecnología criptográfica permite que múltiples entidades, que no necesariamente confían entre sí, colaboren en un cálculo conjunto mientras mantienen sus datos de entrada en privado. El proceso fragmenta los cálculos en componentes distribuidos que se procesan de forma independiente y luego se reensamblan para obtener el resultado final, todo sin exponer la información individual de cada participante.
Una ejemplificación de ello es: Varios hospitales estudian la efectividad de un tratamiento analizando datos de sus pacientes y obtienen estadísticas globales, sin compartir expedientes médicos individuales entre sí.
- **Cifrado Totalmente Homomórfico (FHE):** Representa un avance en criptografía que posibilita realizar operaciones matemáticas directamente sobre datos cifrados, manteniendo la información protegida en todo momento. A diferencia de los sistemas tradicionales, no requiere descifrar los datos para procesarlos, lo que permite análisis y cómputos seguros sobre información sensible sin comprometer su confidencialidad.
Un ejemplo de ello es: Una universidad procesa evaluaciones cifradas de estudiantes a profesores, calculando promedios y estadísticas sin que nadie pueda ver las evaluaciones individuales, manteniendo la privacidad de ambas partes
En cuanto, MPC y ZK ya son utilizados sobre todo en el ecosistema Web3. Pero gracias a los avances en hardware y optimización de algoritmos y computacional se está volteando a ver a FHE. En comparación con MPC, FHE ofrece una protección de privacidad más robusta, mayor flexibilidad computacional y no requiere verificación multipartita. A diferencia de ZK, que es bueno para probar la veracidad de una condición, FHE permite realizar cálculos sobre datos cifrados e incluso entrenar e inferir modelos de aprendizaje automático sobre ellos. Cada tecnología de privacidad tiene su lugar óptimo de aplicación de acuerdo con sus beneficios y limitaciones, contribuyendo en conjunto al avance de la computación privada y criptografía programable en casos de uso reales.
En esta tabla se incluye una breve comparación entre los protocolos y esquemas criptográficos (ZKP, FHE y MPC):

### Referencias
https://mirror.xyz/privacy-scaling-explorations.eth/D8UHFW1t48x2liWb5wuP6LDdCRbgUH_8vOFvA0tNDJA
https://www.zama.ai/post/the-revolution-of-fhe
https://mirror.xyz/privacy-scaling-explorations.eth/wQZqa9acMdGS7LTXmKX-fR05VHfkgFf9Wrjso7XxDzs
https://cryptographycaffe.sandboxaq.com/posts/fhe-01/
https://messari.io/report/fully-homomorphic-encryption-the-holy-grail-of-computing
https://lithiumdigital.medium.com/fully-homomorphic-encryption-a-game-changer-for-data-privacy-and-security-711923351d6f
https://www.zama.ai/post/private-smart-contracts-using-homomorphic-encryption
https://www.ntt-review.jp/archive/ntttechnical.php?contents=ntr201407fa5_s.html
https://www.kairosresearch.xyz/insights/introduccion-a-fhe
https://taiko.mirror.xyz/2O9rJeB-1PalQeYQlZkn4vgRNr_PgzaO8TWUOM5wf3M
https://www.dynamic.xyz/blog/the-evolution-of-multi-signature-and-multi-party-computation
https://inpher.io/technology/what-is-secure-multiparty-computation/
https://eprint.iacr.org/2020/300.pdf
https://securecomputation.org/docs/pragmaticmpc.pdf
https://www.researchgate.net/publication/223098367_Secure_Multi-party_Computation_Made_Simple
https://cronokirby.com/posts/2022/05/explaining-yaos-garbled-circuits/
https://hackmd.io/ZSFlxv7ER0qx9_eiYVMIWw
https://mirror.xyz/privacy-scaling-explorations.eth/wQZqa9acMdGS7LTXmKX-fR05VHfkgFf9Wrjso7XxDzs
https://homomorphicencryption.org/wp-content/uploads/2018/10/CCS-HE-Tutorial-Slides.pdf?ref=blog.sunscreen.tech
https://blog.sunscreen.tech/an-intro-to-fully-homomorphic-encryption-for-engineers/
https://blog.lambdaclass.com/fully-homomorphic-encryption-zero-knowledge-proofs-and-multiparty-computation/
https://medium.com/hackernoon/a-primer-on-zero-knowledge-proofs-892e6e277142
https://academy.bit2me.com/zkp-zero-knowledge-protocol/
https://medium.com/coinmonks/zero-knowledge-proof-explained-1595600ff1cf
https://blog.cryptographyengineering.com/2014/11/27/zero-knowledge-proofs-illustrated-primer/
https://ethereum.org/en/zero-knowledge-proofs/#use-cases-for-zero-knowledge-proofs
https://www.altoros.com/blog/zero-knowledge-proof-improving-privacy-for-a-blockchain/
https://arxiv.org/pdf/2408.00243v1
https://docs.coti.io/coti-documentation/how-coti-works/advanced-topics/garbled-circuits
https://hackmd.io/@Giapppp/SkOg_TKYA
https://www.trevortomlin.com/posts/ot/
https://cronokirby.com/posts/2022/05/explaining-yaos-garbled-circuits/
https://www.researchgate.net/publication/363496697_Survey_on_Fully_Homomorphic_Encryption_Theory_and_Applications
https://rya-sge.github.io/access-denied/2024/10/21/mpc-protocol-overview/#mathematical-foundation-of-mpc