# 2017q3 Homework1 (ternary)

###### contributed by < `hfming225` >

# Balanced Ternary

## Introduction
* Balanced Ternary is a ternary (base $3$) number system in which the digits have the values $–1, 0,$ and $1$.
* Usually, $−1$ is represented as overturned $1$ : $"T"$.
* We can use the Bal3 at the subscript to show which number system it belong to.
>e.g. $T101.11_{Bal3}.$[color=#1aa]

## Conversion
### Bal3 to Dec
$Given\ a\ number$
$A_{N-1}A_{N-2}\cdot \cdot\cdot\cdot A_0.B_1B_2\cdot\cdot\cdot B_{M}$
$,which\ is\ repersent\ in\ Balanced\ Ternary$
$M,N\in \Bbb{N}\ and\ A_k,B_i\in \{T, 1, 0\}$

Use the following formula:
$\displaystyle\sum_{k=0}^{N-1}A_k\times3^{k}+\sum_{i=1}^{M}B_i\times3^{-i}$
We can convert $Bal3$ to $Dec$.
> e.g. $1T0.T01\\=1\times3^2+(-1)\times3^1+0\times3^0+(-1)\times3^{-1}+0\times3^{-2}+1\times3^{-3}\\=9+(-3)+0+(-\dfrac{1}{3})+0+\dfrac{1}{27}\\=5.7\overline{037}_{Dec}\\=5\dfrac{19}{27}$[color=#1aa]

### Dec to Bal3
Now we try to convert $Dec$ back to $Bal3$
Take the number $5\dfrac{19}{27}$
Round to $6$ and $-\dfrac{8}{27}$ (because 5.7... is closed to 6)

Divided it into integer and frcation.

For integer part:
$6\div3=2,\ remainder\ 0\\2\div3 = \dfrac{2}{3}\ round\ to\ 1,\ remainder\ -1\\1\div3=\dfrac{1}{3}\ round\ to\ 0,\ remainder\ 1$
So we get the integer part $1T0$

For fraction part:
$-\dfrac{8}{27}\times3=-8/9=-1+1/9,B1=-1,\\\dfrac{1}{9}\times3=1/3=0+1/3,B2=0,\\\dfrac{1}{3}\times3=1+0, B3=1,B4,B5....=0$
So we get the fraction part $T01$

In conclusion,
$5\dfrac{19}{27} = 1T0.T01_{Bal3}$

## positive and nagetive Number
When we represent number in Binary or Ternary, notice that one more digit is needed to show positive or negative.

But in the $Bal3$, because of $A_k,B_i\in \{T, 1, 0\}$
Let every digit times -1, get the opposite number,
>e.g $1T0.T01$
>$opposite\ number = T10.10T$[color=#1aa]

# Balanced Tarnery Adder
## Three-valued logic
There are three value in Tarnery system.
-1 for false, 0 for unknow, 1 for true.
We can use these vaule to build follow truth table.
## Truth table

### NEG
|$a$|$\bar a$|
|---|---|
|$T$|$1$|
|$0$|$0$|
|$1$|$T$|
>$\bar a = a\times-1$[color=#1aa]
### AND

| $a∧b$ | $\textbf T$ | $\textbf 0$ | $\textbf 1$ |
| ------- | --------| ------- | ------- |
| $\textbf T$ | $T$ | $T$ | $T$ |
| $\textbf 0$ | $T$ | $0$ | $0$ |
| $\textbf 1$ | $T$ | $0$ | $1$ |
>$a∧b=min\ (\ a,\ b\ )$

### OR

| $a∨b$ | $\textbf T$ | $\textbf 0$ | $\textbf 1$ |
| ------- | --------| ------- | ------- |
| $\textbf T$ | $T$ | $0$ | $1$ |
| $\textbf 0$ | $0$ | $0$ | $1$ |
| $\textbf 1$ | $1$ | $1$ | $1$ |
>$a∨b=max\ (\ a,\ b\ )$[color=#1aa]

## Half Adder
With above logic operation, try to build a half adder
By logic design we try to make follow circuit

Now, we need "SUM" and CONS.
### Truth table
| $input \ a$ | $input \ b$ | $ouput \ c_{i+1}$| $output \ s_i$|
| --- | --- | --- | --- |
| $T$ | $T$ | $T$ | $1$ |
| $T$ | $0$ | $0$ | $T$ |
| $T$ | $1$ | $0$ | $0$ |
| $0$ | $T$ | $0$ | $T$ |
| $0$ | $0$ | $0$ | $0$ |
| $0$ | $1$ | $0$ | $1$ |
| $1$ | $T$ | $0$ | $0$ |
| $1$ | $0$ | $0$ | $1$ |
| $1$ | $1$ | $1$ | $T$ |
>In article [Balanced Full Adder](http://homepage.divms.uiowa.edu/~jones/ternary/arith.shtml#fullbalanced)
>Imply that $s_i=a+b=(\ (\ a=-1\ )\ ∧\ (\ b-1\ )\ )\ ∨\ \ (\ (\ a=0\ )\ ∧\ (\ b\ )\ )\ ∨\ (\ (\ a=1\ )\ ∧\ (\ b+1\ )\ )$
>$c_{i+1}=a⊠b=cons\ (\ a,\ b\ )=(\ a\ ∧\ b\ )\ ∨\ (\ (\ a≠-1\ )\ ∧0\ )\ ∨\ (\ (\ b≠-1\ )\ ∧\ 0\ )$[color=#1aa]
## Full Adder
With concept of half adder we can get a full adder.

# Pros and cons
### Advantage
1. Easier than binary to do addition, subtraction and mutiplication.
> Because signed and unsigned are balanced, so subtraction is same as addition with negative.[color=#1aa]
2. Low [Radix Economy](https://en.wikipedia.org/wiki/Radix_economy) which estimate the efficiency of the number system.

### Disadvantage
1. Difficult to make a three type voltage circuit.
>Now our transitor is low voltage, hard to make it in three voltage stablely.[color=#1aa]
2. Division is harder than binary, needed another "trit" to implement.
>[Ternary Division](https://en.wikipedia.org/wiki/Balanced_ternary#Multi-trit_division)[color=#1aa]

# Application
## IOTA, Introduction
- [IOTA](http://www.tangleblog.com/2017/01/25/the-tech-behind-iota-explained/) is a new cryptocurrency that focused on Machine-2-Machine (M2M) transactions.
- It provides **efficient, secure, lightweight, real time micro-transactions without fees.**
- It is **open-source, decentralized cryptocurrency**, engineered for Internet of Things.
- Its real-time micro transactions and providing ecosystem that is ready and flexible for scale.

## IOTA core : Tangle
- IOTA is based on Tangle instead of blockchain.
- Tangle vs. Blockchain
- Tangle retain the blockchain features of the distributed ledger and secure transactions.
- Instead of blockchain, Tangle uses the form of a Directed Acyclic Graph (DAG).
>Directed Acyclix Graph (DAG)
Why is DAG better than blockchain? Because DAG technology enables various features like zero-cost transactions, infinite scalability or offline transactions that blockchain simply cannot do and will neither probably be developed to do.
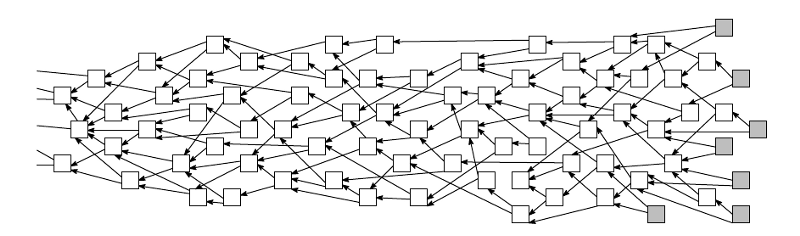
[color=#1aa]

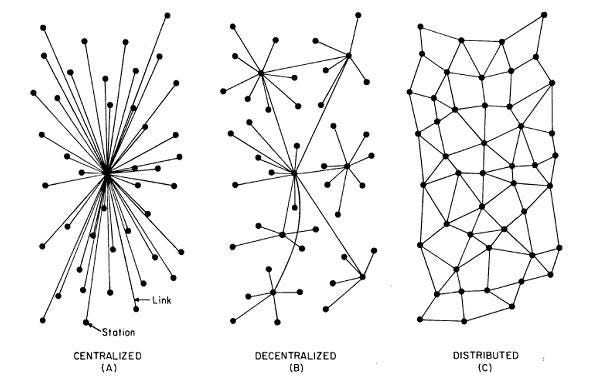
==IOTA structure is like the ( C ) in picture.==

## [Why is iota ternary]
- Radix economy in base on 3 is lowest.
- Ternary 3 states perform transaction very balanced, which is quite helpful to build a self-organizing and self-sustaining network like the tangle.

# Reference
[Wikipedia : Balanced Ternary](https://en.wikipedia.org/wiki/Balanced_ternary)
[The Balanced Ternary Machines of Soviet Russia](https://dev.to/buntine/the-balanced-ternary-machines-of-soviet-russia)
[Balanced Full Adder](http://homepage.divms.uiowa.edu/~jones/ternary/arith.shtml#fullbalanced)
[IOTA討論](https://www.reddit.com/r/Iota/comments/5r72rh/noob_why_3nary_encoding/?st=j8ads8x2&sh=a570be11)
[the tech behind iota](http://www.tangleblog.com/2017/01/25/the-tech-behind-iota-explained/)
[Tangle](http://www.tangleblog.com/what-is-iota-what-is-the-tangle/)
[How IOTA makes bright future for Internet of Things](https://medium.com/@MartinRosulek/how-iota-makes-future-for-internet-of-things-af14fd77d2a3)