:::danger
krzyczcie jesli nasze rozwy nie dzialaja
:::
# Część 1
## 2015

### Zadanie 1
---------
Podaj przykład tekstu i wzorca dla których tablica C[0] = C[1] = C[9] = prawda, a dla pozostałych fałsz. Algorytm Shift-And.

wzorzec:
abcdefgha
do tej pory przeczytany tekst:
abcdefgha

### Zadanie 2
---------
Jak w KMR numeruje się słowa o długości 16?
zaczynamy od slow dlugosci 1...
bierze sie slowa dlugosci 8, zbija w pary i numeruje sie te pary

:::danger
### Zadanie 3
---------
Przedstaw graficznie sieć komparatorów o głębokości <= 4 sortującej wszystkie ciągi 0-1 o długości 7.
Taka sieć nie istnieje. Według Wikipedii optymalna siec komparatorów dla 7 sygnałów ma głębokość 6. ~ S
**bzdety, klamstwa i kalumnie:**
Dla 7 drutów na danej głębokości mogą się wykonać max 3 porównania, czyli dla głębokosci 4 -> 3*4=12. Wiemy, że sortowanie ciagu długośći 7 wymaga więcej, bo ???
:::

### Zadanie 4
---------
Uzasadnij, że obliczenie funkcji pi(Wzorzec[1..m]) w algorytmie KMP ma złożoność O(m).

przechodzimy sie liniowo od 1 do m, zaczynamy od q = 0 i mamy petle while q != 0 and cos tam. No i w tej petli q <- \pi(q), czyli w niej w maleje.
i mamy jakiegos ifa za ta petla na ktorym q rosnie tak? no tak.

q nie wzrosnie bardziej niz m. Ani nie przekroczy 0.

zatem tych spadkow sumarycznie jest tez nie wiecej niz m.
no bo zobczmy ze wzrostow mamy nie wiecej niz m. kazdy taki wzorst jest o 1.
Z drugiej strony sumaryczny spadek nie moze byc wiekszy niz m no bo by przekroczyl 0.

dla wszystkich k te wewnetrzna petle wykonamy najwyzej m razy.
:::info
### Zadanie 5
---------
Przedstaw macierze dla transformacji Fouriera (???)
:::

### Zadanie 7
---------
Czy puste drzewa SPLAYU A i B będą miały równą wysokość, jeśli przeprowadzi się na nich n operacji insert o wartościach:
dla A: 1, 2, 3, ..., n
dla B: n, n-1, ..., 2, 1

taa, bo powstanie kreseczka dla a w prawo, dla b w lewo

### Zadanie 8
---------
Przedstaw drzepiec o n wierzchołkach, w którym usunięcie korzenia wymaga Omega(sqrt(n)) operacji, ew. podaj uzasadnienie dlaczego nie ma takiego drzewca.


w tych drzepcach robimy splity i mergujemy. Ustawiamy tak rangi zeby musiec zawsze wybierac prawy wierzcholek na nowego krola, ktorego trzeba wyciac z jego poddrzewa i zrobic mergea na tym co po nim zostalo.

### Zadanie 10
----------
Ile jest maksymalnie drzew w kopcu:
a) dwumianowym,
b) Fibonacciego.

### Zadanie 11
----------
Złożoność procedury budującej kopiec (wersja z przesun-do-gory()).

O(nlogn) BO TO JEST TO ZLEEE

potencjalnie kazdy wierzcholek moze nas kosztowac log a jest ich n

powinno sie budowac od dolu i wsadzac nowe wierzcholki na korzenie lasu jaki hodujemy i ew przesuwac w dol.

### Zadanie 12
----------
Oszacuj prawdopodobieństwo, że nie będzie żadnej kolizji podczas haszowania funkcją z uniwersalnej rodziny sqrt(n) kluczy w tablicy rozmiaru n.

zmienna losowa
Xij = (h(i) == h(j))

P(Xij) = 1/n

liczba kolizji no to jest suma wszystkich Xij

wszystkich par jest (sqrt n) po 2

czyli EX = (sqrt n) po 2 / n czyli jakas 1/2.

markov

P(X > a) <= EX / a
P(X > 1) <= 1/2
P(X <= 1) > 1/2

### Zadanie 13
----------
Podaj pseudowielomianowy algorytm, który wypisuje dzielniki pierwsze liczby n.

dzielimy przez 2 tyle razy ile się da, potem przez 3,5,7 itd. (jeśli się dzieli to dzielnik pierwszy)

O(sqrt(n) * maksymalny_wykladnik dzielnika)

### Zadanie 14
----------
Jeśli w drzewach AVL' zmienilibyśmy warunek, by poddrzewa mogły różnić się o 2 (nie o 1) wysokością, to czy drzewo n-wierzchołkowe dalej ma wysokość Teta(n)?

BAITT, zwykle avl maja wysokosc log i te tez

### Zadanie 15
----------
Podaj pseudokod rozwiązania problemu LCS.

lsc(x_n,y_m) =
1) x[n]=y[m] 1+lcs(x_n-1, y_m-1)
2) else max(lcs(x_n-1,y_m)x_n,y_m-1))

### Zadanie 16
----------
Przerób kod QuickSorta na QuickSelect (selekcja k-tego elementu zamiast sortowania). Jaką ma złożoność?

xd oczekiwany O(n)

### Zadanie 17
----------
Porównanie kosztów operacji { min, delmin, insert, meld } dla kopców dwumianowych w wersji Lazy i Eager.

lazy - wszystko O(1), tylko deletemin zamortyzowany log
eager - min O(1) meld, deletemin, zamortyzowany log
insert zamortyzowany staly

### Zadanie 18
----------
a) Podaj definicje rzędu drzewa w kopcu Fibbonaciego,
liczba dzieci korzenia
b) Podaj górne ograniczenie na ten rząd,
log, bo fibonacci jest wykladniczy
c) Podaj ideę dowodu tego ograniczenia.
indukcja: i+1szy ma te same dzieci co ity + i-1sze czyli nastepna liczba fibonacciego.

### Zadanie 19
----------
Podaj wzór rekurencyjny algorytmu magicznych piątek dla podziału na 7 elementów.

dzielimy zbior na podzbiory 7 elementowe, dla kazdego z nich znajdujemy mediane i na zbiorze median wywolujemy sie dalej

T(n) = T(n/7) + O(n)

### Zadanie 20
----------
Przykład grafu pełnego o n wierzchołkach takiego, że algorytm Boruvki znajdzie MST w jednej fazie.


## 2016
### Zadanie 1
- kopiec $\Theta(n)$ -> Załóżmy, że w liściach są same wartosću większe od x a w ich rodzicach mniejsze. Trzeba znaleźć minimum ze wszystkich $\frac{n}{2}$ liści, czyli $\Omega(n)$, ale przejrzenie wszytskich wierzchołków na pewno da odpowiedź, więc $O(n)$.
- kopiec dwumianowy - liscie sa polowa wierzcholkow kazdego drzewa, przy tworzeni $T_i$ pod korzeń podpinamy kolejnego syna będącego $T_i$, czyli liczba wierzchołków i liści wzrasta 2 razy
- kopiec Fibonacciego - wszystkie drzewa moga byc pojedynczymi wierzcholkami i trzeba przejrzec je wszystkie

### Zadanie 2

$T(n) = T(2^{2^k}) = T(\sqrt{2^{2^k}}) + c = T(2^{2^{k - 1}}) + c = ... = T(2) + k \cdot c = O(\log {\log {n}})$

### Zadanie 3
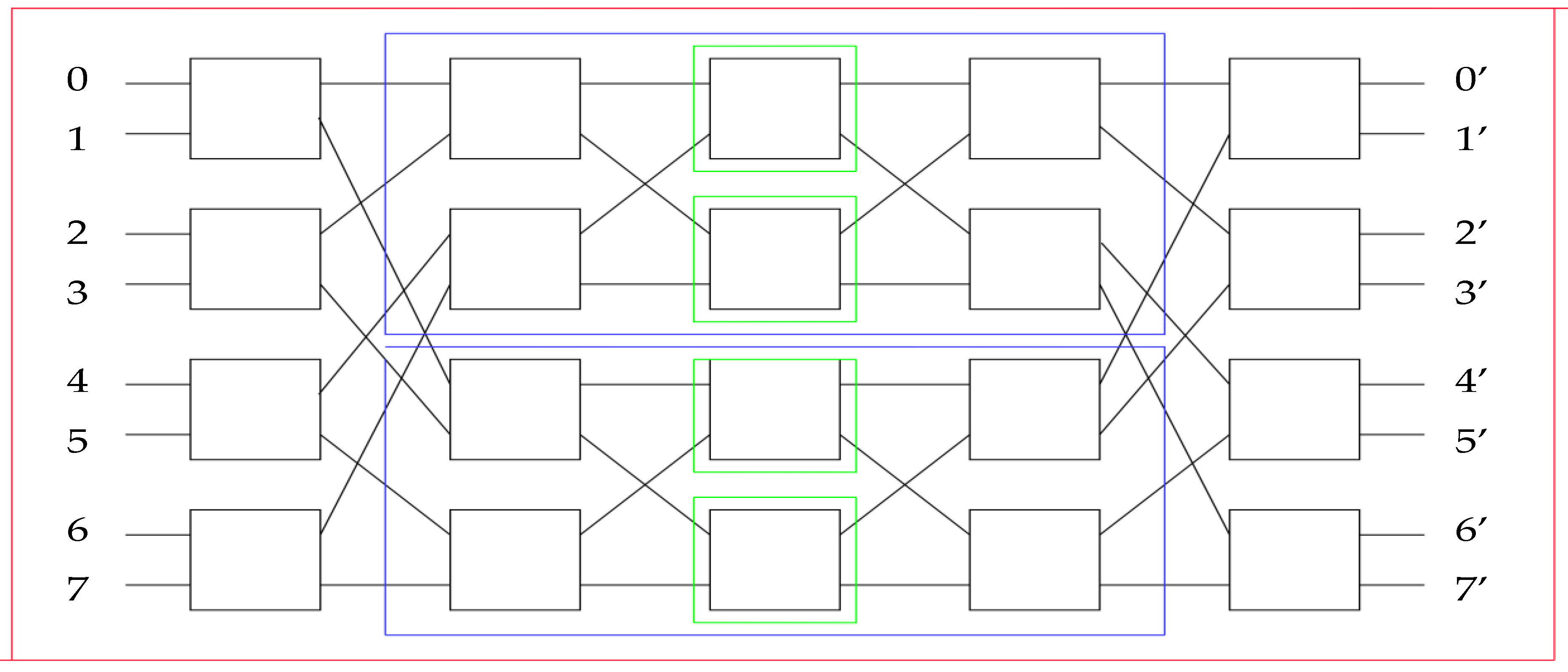
### Zadanie 4
BST po kluczu, porządek kopcowy po priorytetach

p<->s, p<->r, usuń p
:::spoiler Finalne drzewo
:::

### Zadanie 5
Problem with input size n is in NC if there exist constants c and k such that it can be solved in time $O((log (n))^c)$ using $O(n^k)$ parallel processors.
Zwykłe dodawanie pisemne xd.
### Zadanie 6
insert(x) robi splay(x) - dzieli drzewo na $T_1, T_2$ ($T_1$ o kluczach mniejszych niż x, $T_2$ o kluczach większych; ustawiamy x jako korzeń nowego drzewa a $T_1, T_2$ na jego dzieci.

Tak, np. drzewo powstałe przez insert(1), insert(3), insert(2).

### Zadanie 7

Wybieramy losowo próbkę R (rozmiaru $n^{\frac{3}{4}}$), który można liniowo posortować względem n). Znajdujemy w R elementy L i H, takie że z dużym prawdopodobieństwem mediana znajduje się w niewielkim zbiorze P elementów większych od L i mniejszych od H. Jeżeli mediany nie ma w P lub P jest zbyt duże to powtarzamy losowanie.
:::spoiler
:::
### Zadanie 8

Shift i and na krótkich wzorcach (mieszczących się w słowie maszynowym) jest wykonywany w O(1). Dla dłuższych wzorców operacje te byłyby proporcjonalne do długości wzorca i algorytm nie byłby efektywny.

### Zadanie 9

Wstawiamy x do struktury V. Jeśli w V nic nie ma, to ustaiamy V.min i V.max na x i koniec.
Wpp. sprawdzamy, czy x < V.min, jeśli tak to swap(V.min, x). Jeśli w klasterze high(x) nic nie było, to wstawiamy high(x) do summary. W obu przypadkach wrzucamy low(x) do klastera high(x).

$O(\log{\log{x}})$ - zależność z zadania 2

### Zadanie 10

2k-2. po przeczytaniu całego wzorca cofamy sie o jedno ab. 2k-1 jest niemożliwe, bo jeżeli po a nie wystąpiło b to musimy wrócić do poprzedniego a.
### Zadanie 11

$O(n)$ - wstawianie elementów na kolejkę,
$O(m \cdot (\log*{n}+ \log{n})$ - dla każdej krawędzi wyciągamy ją z kolejki (log) i dla obu jej końców wołamy find (log*).

### Zadanie 12

matmult(d[0,1,2,..,n]){
for i = 1,..,n
    m[i][i] = 0
for i = n-1, .., 1
    for j = i + 1, .., n
        m[i][j] = inf
        for k = i, .., j-1
            m[i][j] = min(m[i][j], m[i][k] + m[k+1][j] + d[i-1] * d[k] * d[j])
}

### Zadanie 13
Będziemy to robić warstwami dla obu drzew naraz - pierwsza warstwa to wierzchołki odległe od korzenia o h - wysokość drzewa, druga - o h - 1 itd.
- Zaczynamy od warstwy 1. Każdy wierzchołek jest liściem i dostaje etykietę 1. Sprawdzamy, czy w obu drzewach jest ich tyle samo.
- Przchodzimy do wyższej warstwy, dla każdego wierzchołka z tej warstwy tworzymy listę, na którą wrzucamy etykiety jego dzieci w kolejności rosnącej (posortowaliśmy je w poprzedniej fazie). Nadajemy etykiety wierzchołkom z nowej warstwy tak, żeby wierzchołki o takich samych listach miały takie same etykiety a o różnych różne (radix sort). Sprawdzamy, czy nowe listy etykiet są takie same.

Jeśli doszliśmy do korzenia to sukces, wpp. smuteczek.

O(n), bo każdy wierzchołek obsługujemy co najwyżej raz (radix sort jest liniowy, (każda warstwa zajmuje O(*liczba wierzchołków w warstwie*) czyli łącznie n)).

### Zadanie 14
Zamortyzowany $O(|\sigma|)$ - każdy union dostaje 2 j.k. - 1 na operacje niskiego rzędu, drugą daje podpinanemu wierzchołkowi. Find dostaje 1 jednostkę - na przejście na wyższy poziom i podpięcie pod lidera. Pozostałe wierzchołki opłacają podpięcia z własnej kieszeni.

Niezamortyzowany - $\log {n} \cdot$ #findów + #unionów

### Zadanie 15

Mamy plrcak o maksymalnym udźwigu W i przedmioty {1,2,..,n} (przedmiot i ma wartość $v_i$ i wagę $w_i$). Chcemy znaleźć multizbiór przedmiotów maksymalizujący wartość i nie przekraczający wagi W.

Algorytm :
Plecak(w) - zwraca maksymalną wartość plecaka o udźwigu w

- Dla w = 0
Plecak(w) = 0
- Wpp.
Plecak(w) = $max_{w_i \le w}$ (Plecak(w - $w_i$) + $v_i$)
### Zadanie 16

Chcemy pomnożyć dwa wielomiany, ale nie umiemy. Umiemy mnożyć liczby, a wielomiany n-tego stopnia można zapisać jako zbiór n + 1 punktów. Dwa wielomiany w postaci listy punktów (o tych samych współrzędnych x-owych) łatwo pomnożyć. Problemem jest konwersja wielomianu z postaci współczynnikowej na punktową i z powrotem. Umiemy konwertować wielomiany stopnia 0 i dla wielomianu $P(x) = a_0 + a_1 + ... + a_n$ umiemy skonstruować wielomiany A i B takie, że $P(x) = A(x^2) + xB(x^2)$, $A(x) = a_0 + a_2x+ a_4x^2 + ... + a_n x^{n/2}$, $B(x) = b_0 + b_2x+ b_4x^2 + ... + b_n x^{n/2}$. Chcemy tak dobrać punkty, żeby po skwadraceniu liczba punktów się zredukowała o połowę. Wybieramy $e^{2\pi i k / n}$.

### Zadanie 17
Budowa od dołu - 2 kopce o wysokości h + nowy wierzchołek = kopiec o wysokości h + 1.

for i = n / 2, i >= 1, i--
    przesun_niżej(K, i)

### Zadanie 18

Kopce Fibonacciego to las drzew o porządku kopcowym. Od każdego wierzchołka możemy (bez konsekwencji) odciąć co najwyżej jednego syna, odcięcie drugiego powoduje odcięcie samego wierzchołka (operacja odcinania umieszcza odcinane poddrzewo w lesie). Zauważmy, że jeśli wszystkie wierzchołki na ścieżce danego wierzchołka do korzenia już straciły jednego syna i odcinamy ten dany wierzchołek to kaskadowo odetniemy wszystkie wierzchołki na ścieżce.

### Zadanie 19
Drzewo o wysokości h musi mieć co najmniej F(h) wierzchołków:
$F(1) = 1, F(2) = 2, F(h) = 1 + F(h-1) + F(h-2)$.
Można łatwo sprawdzić, że $F(8) < 67 < F(9)$, czyli odpowiedź to 8.

### Zadanie 20

Fakt z wykladu: 1/2. Bo to funkcja z rodziny uniwersalnej.

## 2017
::: info
### Zadanie 16
:::

::: info
### Zadanie 17
no bo te macierze noo.
:::

:::danger
### Zadanie 12
rotacje dla wszystkich wierzchołków na drodze: »1.4405log(n+2)]
:::
### Zadanie 2

Kopiec, który ma $\le 500$ elementów nie zawiera drzew o rzędzie $> 8$ (bo drzewo o rzędzie 9 ma 512 elementów).
Join wykona się nie więcej razy niż liczba różnych drzew występujących w którymkolwiek kopcu (czyli u nas 9).
Przykład wykonujący 9 joinów :

     101111111 
meld 011111111
   = 1001111111
<kolejne bity mówią czy drzewo o danym rzędzie znajduje się w kopcu>   

### Zadanie 3

### Zadanie 4

(1, n), (2, n-1), ..., (n, 1). Każdy wierzchołek można usunąć bez rotacji.

### Zadanie 5

Adwersarz ma 4 zbiory: nieznane, wygrywy, przegrywy i śmietnik. Adwersarz będzie mówić, że jeżeli będziemy porównywać wygrywa z czymkolwiek to wygryw, przegrywa z czymkolwiek to to cokolwiek.
### Zadanie 6

Przykład: powstały dwa zlepki długości n/4-1

### Zadanie 7

Hoare -> losowy
5 -> dzielimy zbior na zbiorzątka po 5 elementów, na nich liczymy medianę w czasie stałym, i te mediany to nasz nowy zbiór i tak dalej...
Lazy Select -> R[x] $x = kn^{3/4}$
R to posortowana tablica losowo wybranych $n^{3/4}$ elementów.
Dzielimy tablicę na zbiór P $2\sqrt{n}$ punktów wokół R[x] i pozostałe punkty.

### Zadanie 8
a) abbbbb..b
b) aabbbb..b

### Zadanie 9

### Zadanie 10
Można ukorzenić drzewo w O(n) i wtedy to samo.
### Zadanie 11

Dla każdego prefiksu wzorca trzymamy informację, czy jest sufiksem do tej pory trzymanego tekstu na wektorze c (c[j] = czy j-ty prefiks jest sufiksem). Jeśli wzorzec jest dość mały, żeby zmieścił się na jednym słowie maszynowym, to możemy go przesunąć w prawo o jeden i ustawiamy lewy bit na 1. Potem chcemy sprawdzić, czy nadal nam się zgadzają te wzorce, więc and z R_p (R_p[i] = czy ita litera wzorca to p), gdzie p to następna litera tekstu.

### Zadanie 13
::: info
### Zadanie 14
:::
### Zadanie 15

O(n)
funkcję pierwotną i funkcje wtórne.

### Zadanie 18
rzad wierzcholka to wysokosc tego wierzcholka po wykonaniu samych unionow. grupa rzedu to log* rzad. po co pamietac rzad, to jest tylko do dowodu... max rzad to log i potrzebujemy na niego loglog bitow
### Zadanie 19
zeby sie pozbyc dodatkowych wywolan rekurencyjnych z succ. bo musimy wiedziec czy warto szukac w naszej kepce czy nie i znajdziemy pierwszego niepustego klastra (szukajac succ na summary) i poprosimy o jego minimum.
### Zadanie 20

Znalezlismy dr i dl: odleglosci najblizszych punktow z prawej i lewej polowy. sortujemy po y punkty z pasa niepewnosci i dla kazdego punkciku sprawdzamy go z 7 nastepnymi.

## 2018
### Zadanie 1
zbior nieterminali z ktorych mozna wyprowadzic podslowo w od i do j.

### Zadanie 3
dzielimy liczby w pary i porownujemy zapisujac zwyciezcom przegrywow i tak dalej az nie zostanie jeden wygryw. drugi najwiekszy musial przegrac ze zwyciezcą wiec jest na jego liscie i wystarczy ze wsrod log ludzi na liscie wygrywa go znajdziemy.
### Zadanie 5

Bierze etykiete i laczy z etykieta przesunieta o 7.

### Zadanie 7
1 < 2 < 3
bardzo znany fakt:
f(x) = O(g(x)) i g(x) != O(f(x))
f(x)^g(x) > g(x)^f(x)

### Zadanie 8

wrzucasz do liscia i przesuwasz do gory

### Zadanie 9
cut - odetnij wierzcholek i wloz go jako nowe drzewo kopca.
decrease key jest szybszy, ale w delete min potencjalnie wiecej rzeczy naprawimy.
::: info
### Zadanie 11
:::

### Zadanie 12
logn

### Zadanie 13

insert(V, x):
if V.min == None
    V.min = V.max = x
    return
if x < min
    swap(x, min)
if x > max 
    max = x
if V.cluster[high(x)].min == None
    insert(V.summary, high(x))
insert(V.cluster[high(x)], low[x])

### Zadanie 14

### Zadanie 16

3k-2

### Zadanie 17

ppb 1/m = 1/2n, par n po 2
suma EX = n - 1

### Zadanie 18

nieee bo dwumianowe sa wielodzietne. wlasciwa jest lista dzieci plus wartosc

### Zadanie 19
wszystko mod m
liniowo - na najblizsze wolne
kwadratowo - na c1 * i + c2 * i^2
podwojne - suma dwoch hashy (h1(k)+ih2(k))

## 2019

#### Zadanie 1
tak co za obrzydliwy bait, w rbtree wymaga dokladnie 3

### Zadanie 2
dla jednego elementu |P| = 1. dla dwoch losowe rzeczy sie dzieja i moze akurat tak sie wydarzylo ze warunki sa spelnione.

### Zadanie 3

nic nam nie psuje, przejmujemy sie jesli suma kwadratow wszystkich kubelkow nie jest O(n)

### Zadanie 4
:((((

### Zadanie 5
Możemy podzielic nasz ciag na pol.
Znany fakt:
przesuniecie cykliczne calosci to przesuniecie ciagow dlugosci pol o tyle samo co startowego.
Polaczmy te mniejsze ciagi pierwszymi przelacznikami i wstawmy pierwsza polowke do pierwszego rekurencyjnego wywolania a druga do drugiego.
O(log(n))

### Zadanie 6

Przesuwanie dziury bo:
- w przesuwania liscia porownujesz go z dziecmi i dzieci miedzy soba wiec 3log porownan
- porownujesz tylko dzieci miedzy soba log i wstawiasz ostatni element na miejsce ktore sobie znalazla dziura na dole (przesun nizej) czyli wsm 2log

### Zadanie 7

insert(V, x)
if (v.min == None)
    V.min = x
    V.max = x
    return
if (v.min > x)
    swap(V.min, x)
if (V.max < x)
    V.max = x
if V.cluster[high(x)].min == None
    insert(x.summary, high(x))
insert(x.cluster[high(x)], low(x))

### Zadanie 8

n/2 nieparzyste staja sie parzyste a parzyste duze sie pokrywaja z parzystymi malymi.
Po ludzku: jak mnozymy dwa pierwiastki z 1 to dodajemy ich katy, jak kwadracimy to mnozymy razy dwa i tak sie sklada ze polowa sie zzera

### Zadanie 10

n-1 bo jak mamy zdegenerowane drzewo np podczas wsadzanie 1, 2 ... n to musimy przerotowac wszystko

### Zadanie 11

xij == czy i j koliduja
E(xij) = 1/300
suma E = 30 po 2 * E(xij)

### Zadanie 12

wysokosc moze byc potencjalnie n-1.
Bo mozemy laczyc paleczke dlugosci i z paleczka dlugosci 1, tak ze paleczka1 jest korzeniem i mozemy jej odciac dzieciaczka bez linii latorosli. w taki sposob mozemy tworzyc paleczki dlugosci n.

[link do wizualizacji](https://stackoverflow.com/questions/14300256/how-to-show-fibonacci-heap-with-n-nodes-can-have-height-n)

### Zadanie 13

lepsze to niz liniowa ale i tak tworza sie zlepki i podwojne haszowanie byloby lepsze

### Zadanie 14

rozwaz mnostwo przypadkow
grafika w starym cormenie, 723 strona, 4 przypadki

### Zadanie 15

Dla każdego u tz 1/3 <= u <= 1/2, jesli podzielimy tablice na u i 1 - u, to $n \log_{(u)^{-1}}{n} \le czas\le n \log_{(1-u)^{-1}}{n}$.
Schodzimy log razy wykonujac n porownan (co najmniej mniejszy log, co najwyzej wiekszy).
$\Theta(n\log{n})$

### Zadanie 16


### Zadanie 17

rzad to wysokosc gdyby byly wykonywane same uniony, grupa to rzad log*. przy optymalizacji uniona max rzad to log wiec bitow loglog

### Zadanie 18

$\pi(1)=0$
$\pi(2)=1$
$\pi(3)=0$
$\pi(4)=1$
$\pi(5)=2$
$\pi(6)=2$
$\pi(7)=3$
$\pi(8)=4$
$\pi(9)=5$
$\pi(10)=6$
$\pi(11)=7$
$\pi(12)=8$

### Zadanie 19

Gdyby istnial algorytm ktory robi w mniej to sortowanie z jego pomoca byloby szybsze niz nlogn: dolna granica.

### Zadanie 20

c to jest wektor taki ze c[r] = czy prefiks wzorca dlugosci r jest sufiksem do tej pory przeczytanego tekstu . dla kazdej literki mamy tablice R[i] = czy r jest ita literka wzorca. zeby obsluzyc nastepna literke wystarczy przesunac c o jeden w prawo, na najbardziej lewe miejsce dac 1 i and z R[przeczytana literka].

## 2021

### Zadanie 1
${n \choose 2} \cdot \frac{1}{n^{\frac{3}{2}}}$ = $0,5 \cdot n^{\frac{-1}{2}} \cdot (n-1)$

### Zadanie 2

budowa od dolu: 1a, 1b, 1c. 1b, 1c to nasze mini kopczyki, które łączymy z 1a jako korzeniem.
Usuwamy 1a.
wersja lisc: 1c zostaje korzeniem i porzadek zostal zaburzony.

wersja dziura: algorytm moze wybrac 1c na wieksze dziecko i jw.

### Zadanie 3

kopiec min, k pełnych poziów + 1 liść na k+1-poziomie
Jeśli wierzchołek jest lisćiem, to istnieje k-1 elementów mniejszych od niego(wszytskie na śceżce od tego liścia do korzenia), czyli 1, 2, ..., k - 1 na pewno liśćmi nie są.

::: info
### Zadanie 4
:::

### Zadanie 6
Insert(i, S) - Splay(i, S), załóżmy, że wyniósł do korzenia następnik (dla poprzednika analogicznie)
x = make_splay(i)
x.left = S.left, S.left = null, x.right = S
return x

### Zadanie 7
53 = 32 + 16 + 4 + 1
35 = 32 + 2 + 1
4 : 1+1, 2+2, 4+4, 32+32

### Zadanie 8
O wysokość najwyższego drzewa (jeśli każdy na ścieżce już stracił 1 syna), czyli n.


### Zadanie 10

aaaa aaa bcde

### Zadanie 11

dla wszystkich i sprawdzimy pierwszy raz warunek petli while, dla parzystych i drugi raz, ...

$\Theta(n\log {n})$

### Zadanie 12

Successor(V, x):
     if x < V.min:
         return V.min
    i = high(x)
    if low(x) < V.cluster[i].max:
        j = Successor(V.cluster[i], low(x))
    else
        i = Successor(V.summary, i)
        j = V.cluster[i].min
    return index(i, j)

### Zadanie 14


### Zadanie 15

a) n/(2^r) - podpinamy pod korzeń jakieś drzewo o rzędzie r - 1, ono ma >= 2^{r - 1} wierzchołków (fakt z wykładu), czyli to do czego podłączamy też przynajmniej tyle, zatem n >= x * 2^r (gdzie x - liczba wierzchołków o rzedzie r)
b) n/r, wszystkie wierzchołki z warstwy k muszą mieć pod sobą co najmniej po jednym wierzchołku z warstwy k-1.

### Zadanie 16

### Zadanie 17

ciągi $A_1, A_2, ..., A_n$ długosći $d$

lista_ciagow - lista z $A_1, A_2, ..., A_n$
kubelki[26] - puste listy

for i = d, .., 1
    for j = 1, .., n
        A = lista_ciagow.pop_front()
        kubelki[A[i]].push_back(A)
    clear(lista_ciagow) 
    for(t = 1, .. 26)
        lista_ciagow = concat(lista_ciagow, kubelek[t])
        kubelek[t] = null
return lista_ciagow
        

### Zadanie 18

$\log_{\frac{7}{10}}{n}$

### Zadanie 19

mij = min po i <= k < j (mik + mk+1j + di-1dkdj)

### Zadanie 20
431

## 2022

### Zadanie 1
$f_0 = a, f_1 = b, f_2 = c, f_i = f_{i-2} + f_{i-3}$ dla $i > 2$ podaj macierz którą będziemy potęgować

[010]
[001]
[110]

wynik mamy na dole wektora

### Zadanie 2
Podaj koszt operacji meld w kopcu dwumianowym wersji lazy i w kopcu Fib

O(1) bo laczymy dwie listy i aktualizujemy min z dwoch minow

### Zadanie 3
Napisz w pseudokodzie operacje prev(k) znajdowania poprzednika klucza k w strukturze van Emde Boosa

prev(V, x):
    if (V.min > x)
        ret inf
    if (V.max < x)
        ret V.max
    i = high(x)
    if (V.cluster[i].min < x)
        j= prev(V.cluster[i], low(x))
    else
        i = prev(V.summary, high(x))
        j = V.cluster[i].max
    ret index(i, j)
    

### Zadanie 4
Rozwiąż równanie rekurencyjne:
$T(n) = 1$ dla małych n
| $T(n) = T(\lfloor \alpha*n \rfloor) + T(\lfloor \beta*n \rfloor) + O(n)$ wpp
dla pewnych stałych $\alpha,\beta$ takich że $\alpha+\beta<1$

rozpisujac rownanie rekurencyjne dostaniemy ciag geometryczny cn(1 + (alfa + beta) + (alfa + beta)^2 + ...), który można ograniczyć z góry szeregiem geormetrycznym, którey zbiega do jakiegos d*cn.

### Zadanie 5
Który z dwóch poniższych ciągów kontrolnych dla metody kwadratowej usuwania kolizji w haszowaniu metodą adresowania otwartego, jest Twoim zdaniem lepszy? Odpowiedź koniecznie uzasadnij.
- $h(k,i) = (h'(k)+37i+47i^2)$%$1000$
- $h(k,i) = (h'(k)+375i+475i^2)$%$1000$

pierwsza jest fajna a druga glupia bo mnozymy razy wielorotnosci 5 i robimy modulo wielokrotnoscia 5, wiec wspolczynniki drugiej sie sybciej zacyklaja (dla liczb pierwszych dlugosc cyklu to m, dla liczb nie wzglednie pierwszych z m znacznie mniej).
### Zadanie 6
Podaj przykład grafu G, w którym wszystkie krawędzie mają różne wagi i dla którego algorytm Prima i Boruvki mogą znaleźć różne minimalne drzewa spinające lub uzasadnij, że taki graf nie istnieje

nie istnieje bo jest dokladnie jedno MST dla grafow z roznymi wagami.

### Zadanie 7
Podaj definicje i przykład uniwersalnej rodziny funkcji haszującej

ax + b mod p mod m
a - z*p, b - zp, p pierwsze > |U|

dla kazdej pary roznych liczb a i b, liczba funkcji, która zwraca ta sama wartosc dla a i b jest mniejsza rowna |H|/m

### Zadanie 8
Opisz algorytm tworzenia kopca, którego złożoność określa równanie $T(n) = O(\sum_{i=1}^nlogi)$. Czy jest to najszybszy możliwy algorytm tworzenia kopca? Odpowiedź uzasadnij

To jest ta glupia wersja O(nlog n), napracowalismy sie strasznie i nic z tego nie mamy.
Otoz bierzemy sobie kopiec i nowy element wstawiamy jako ostatni lisc po czym windujemy go do gory.
dobra wersja O(n).

### Zadanie 9
Podaj sieć przełączników o optymalnej głębokości (z dokładnością do stałego czynnika), realizującą wszystkie przesunięcia cykliczne

wejsciowe druty $i$ i $n/2 + 1$ łączymy przełącznikami, z których wypuszczamy jeden drut do gornej a drugi do dolnej sieci(n/2).

### Zadanie 10
Używamy algorytmu KMP do wyszukania wzorca $P=(aba)^k$ w tekście T (k jest pewną stałą, a nawiasy nie są znakami wzorca). Załóżmy, że T zawiera podsłowo $c(aba)^{k-1}d$. Ile porównań znaku d z tego podsłowa ze znakami wzorca wykona KMP

k

### Zadanie 13
W jakim czasie działa algorytm Djikstry, jeśli kolejka priorytetowa zaimplementowana jest przy pomocy kopców Fib?

m + n log n
boo modyfikacja wierzcholka na kolejce jest oczekiwana stala
a usuwanie min jest oczekiwane log

### Zadanie 14
Opisz ideę algorytmu znajdowania mediany opartego na idei próbkowania losowego.

Losujemy z S z powtórzeniami n^(3/4) elementów do zbioru R ktory sortujemy. x = kn^{-1/4}. l = max(1, podloga(x- sqrt(n))), h = min (n, podloga(x = sqrt(n))).
ll = |{y in S | y < R[l]}|
P = {y in S | R[l] <= y <= R[h]}
sprawdzamy czy k jest w P i czy |P| <= 4n^{3/4} +2, jesli tak to fajnie, sortujemy P i mamy wynik, jesli nie to powtarzamy zabawe.

### Zadanie 15
Napisz procedury realizujące operacje słownikowe na drzewie splay, wykonujące co najwyżej stałą liczbę operacji splay i stałą liczbę operacji niskiego rzędu.

find - splay x, przeczytaj korzen,
insert - splay x, w zaleznosci od tego czy poprzednik czy nastepnik jest korzeniem odcinamy mu dziecko i przypinamy to dziecko oraz stary korzen jako poddrzewa xa (x staje sie korzeniem)

delete - splay x odetnij korzen i zlacz poddrzewa:
splay x na lewym, wiemy ze wszystkie wartosci sa od niego mniejsze, wiec jego poprzenik ma tylko jedno dziecko (lewe) i jako prawe poddrzewo mozemy mu wsadzic prawe poddrzewo x.

### Zadanie 16
Narysuj minimalne (pod względem liczby wierzchołków) drzewo AVL o wysokości 4. Przez wysokość rozumiemy liczbę krawędzi pomiędzy korzeniem a najbardziej oddalonym liściem.


### Zadanie 17
W algorytmie wyznaczającym optymalną kolejność mnożenia macierzy, opartym na programowaniu dynamicznym, wyliczana jest wartość $m_{ij}$ równa optymalnemu kosztowi obliczenia iloczynu macierzy $M_i \times \dots \times M_j$. Podaj sposób obliczenia wartości $m_{ij}$.

mij = min (mik + mk+1j + di-1dkdj)

### Zadanie 18
Przekształcanie wykonywane algorytmem FFT można przedstawić równaniem $\bar{y} = V \cdot \bar{a}$. Napisz jakie wartości mają wektory $\bar{y}$ i $\bar{a}$ oraz $V$.

y - wartosci wielomianu w punktach omega[i]
a - wspolczynniki wielomianu
V - macierz V[j][k] = omega ^jk

### Zadanie 19
Jakie jest czas budowy dwupoziomowego słownika statycznego? Odp. uzasadnij.

oczekiwany liniowy, bo bedziemy srednio mniej niz 2 razy losowac kazda funkcje.

### Zadanie 20
Ile liczb wypisze program

while n > 1
    i <- 0
    while n > 1
        i <- i + 1
        n <- n / 2
    wypisz i
    n <- i

log*n
czyli ile razy mozna zlogarytmowac liczbe

## 2017 Poprawka

### Zadanie 2

o n. byla jedna zdegenerowana kreska zalobinkow i my ja rozwalilismy atakujac liscia.

### Zadanie 3
tak bo find wywoluje splaya a on moze napsuc

### Zadanie 4

dokladnie jeden bo nie mozemy przerotowac zadnego wierzcholka bo priorytety

Rekurencyjnie nam sie generuje jedno konkretne drzewo od korzenia: wybieramy wierzcholek o maksymalnym priorytecie i ze wzgledu na jego klucz rodzielamy wierzcholki na dwa zbiory: wiekszych i mniejszych, wywolujemy sie na nich rekurencyjnie.

### Zadanie 5

mamy ciag n liczb (punkt w n wymiarach) i sprawdzamy czy wszystkie liczby sa parami rozne.
w modelu zwyklych $\Omega(n^2)$

### Zadanie 6

ih1(x) + h2(x)
najlepsza metoda adresowania otwartego bo w odroznieniu od metody liniowej i kwadratowej nie robi zlepkow

### Zadanie 7

T(n) = T(3/10) + T(7/10) + O(n)

### Zadanie 8

$\pi(1)<-0$
k <- 0
for q=1,..,m
while (k > 0 and P[q] != P[k + 1])
k <- \pi(k)

if P[k+1] = P[q]
k++
\pi(q) <- k

### Zadanie 9

### Zadanie 10

Mamy plecak o maksymalnym udźwigu W i przedmioty {1,2,..,n}. Przedmiot i ma wartość v_i i wagę w_i. Chcemy zmaksymalizować łączną wartość przedmiotów w plecaku (nie możemy przekroczyć wagi W).

f(w, j) - maksymalna wartość z przedmiotów {1,2,..,j} nieprzekraczająca wagi w

f(w,j) = 0 dla w=0 lub j-0
max(f(w-w_j) + v_j, f(w,j-1)) wpp

O(nW) - pseudowielomianowa, bo zależy nie tylko od rozmiaru danych (#przedmiotów), ale też od parametru - udźwigu plecaka

### Zadanie 11

krotkie wzorce na dowolnych tekstach dokladnie mniejszych niz slowo maszynowe bo wykonujemy operacje maszynowe

### Zadanie 12

Diff(h) = PełneDrzewo(h - 1) - Minimalne(h - 2)
Minimalne(h) = Minimalne(h - 1) + Minimalne(h - 2) + 1
$E^3 - E^2 - E - 1 = 0$
$Diff(h) = 2^{h} - 1 - (1.8...)^{h-2}$
więc diff jest wykładniczy od wysokości, więc $Theta(n)$

### Zadanie 13
Usuwamy korzeń drzewa, na którego wskazuje MIN, nawlekamy jego dzieci na listę drzew, łączymy drzewa z listy o tym samym rzędzie.
pesymistycznie O(n), zamortyzowana O(log n).

::: warning
### Zadanie 14

Problem jest NP-zupełny - np trudny i np

LIS - najdluzszy podciag rosnacy O(nlogn)
NP - tak
NP-trudny - nie, zakladajac hipoteze ze P jest rozne od NP, bo istnieje rozwiązanie w czasie wielomianowym

:::

### Zadanie 15

O(n), musimy zapamiętać h oraz h_1, h_2, ..., h_m oraz m_1, m_2, ..., m_m (gdzie m - rozmiar tablicy z pierwszego poziomu, m_i - itej z 2 poziomu), funkcje pamiętamy w postaci a,b,p h(x) = ((ax+b) mod p ) mod m_i

### Zadanie 16

Dla kazdej pary ppb = 1/1000
par jest 100 po 2
wartosc oczekiwana = (100 po 2) / 1000

### Zadanie 17

### Zadanie 18

### Zadanie 19
Do szybkiego znajdowania succesora -

### Zadanie 20


## 2018 Poprawka

### Zadanie 1

$n^{3/4} / n \cdot 100$

:::info
### Zadanie 2

$\Theta(n^{log_k({2k - 1})})$, czyli u nas $\Theta(n^{log_3(5)})$.
:::

### Zadanie 3
Jeżeli sieć sortuje poprawnie każdy ciąg 0-1, to sortuje też poprawnie każdy inny.

d-d: Wiemy, że jeśli dla a_1, a_2, .., a_n sieć zwróci b_1, b_2, .., b_n, to dla dowolnej f niemalejącej dla f(a_1), f(a_2),...,f(a_n) zwróci f(b_1), f(b_2),...,f(b_n).
Załóżmy nie wprost, że zasada 0-1 nie działa (ale sortowanie 0-1 tak). Niech S - dowolny ciąg niedziałający i s_i < s_j, ale s_j wyjdzie przed s_i.
Weźmy f(x) = (x>s_i). Wtedy dla f(s_1), f(s_2),... mamy f(s_i) < f(s_j), więc f(s_i) wyjdzie przed f(s_j). Sprzecznosc.

### Zadanie 4
niezamortyzowane:
a) log (w drzewie wysokosci h >= 2^h wierzchołków -> indukcja)
b) n (prosta kreska)

### Zadanie 5

mamy rubryke minimum do której dostep jest O(1)

### Zadanie 6
Może. (Na rysyunku napisane tylko priorytety.)

### Zadanie 7

zauwazmy ze jak odwrocimy drugi ciag i dokleimy do pierwszego to z dwoch posortowanych mamy jeden bitoniczny i mozemy go wlozyc do bit sorta.
(Dlatego najpierw robimy odwrócona półczyszczącą zamiast zwykłej)

### Zadanie 8

sufit(3/2n) - 2

Porównujemy parami, mniejsze wrzucamy do zioru mini, wieksze do maxi. Szukamy w maxi max a w mini min (liniowo) i ewentualnie porownujemy je z 1 samotnym elementem, który nie miał pary (dla n niaparzystego).

(n/2) + (n/2 - 1) * 2

### Zadanie 9
Szukamy elementu w tablicy, wyrzucamu go i zaznaczamy, że miejsce było kiedyś zajęte. Jeśli takich znaczników zrobi się za duzó, przeorganizowujemy tablicę.

### Zadanie 10

P(w,j) - najwieksza wartosc zawartosci plecaka zawierajacego elementy z {1,..,j} bez powtorzen o masie <= w

P(w,j) = 0 dla w=0 v j=0
P(w,j) = max(P(w-w_j,j-1)+v_j, P(w,j-1)) wpp.
Złożoność O(nW) - pseudowielomianowa, bo zależy też od udźwigu plecaka W.

### Zadanie 11
Weźmy n = $2^{2^k}$. Wtedy sqrt(n)=$2^{2^{k-1}}$. O(1)=c.
T(n) = c + 4c + 16c + ... + 4^{k-1}c + 4^k = c (4^k-1)/3 + 4^k =
k to jest loglog wiec to cale jest \Theta(log n)

### Zadanie 12
- pesymistyczna:
T(n) = T(sufit(n/3)) + T(2/3 n) + O(n)
O(nlogn)
- optymistyczna:
Jeżeli chodzi o znalezienie k-tego elementu i koszt selecta :
T(n) = T(sufit(n/3)) + T(1/3 n) + O(n)
O(n)
Jeżeli chodzi o samo pseudomed :
T(n) = T(sufit(n/3)) + T(1/2 n) + O(n), bo w pseudomed szukamy n/2-go elemetu, więc nie trafimy do zbioru o mocy < n/2
O(n)

### Zadanie 13

mamy T[1...n], P[1..m], pi

q <- 0
for k = 1,..,n
while q>0 and T[k]!=P[q+1]
q<-pi(q)
if T[k] == P[q+1]
q++
if q == m
print(Znaleziono z przesunięciem k-m)
q <= pi(q)

O(n) (z liczenie pi O(n+m))

### Zadanie 14

mij - minimalny koszt pomnozenia macierzy od i do j
mij = min (mik + mk+1j + di+1dkdj)

$\Theta(n^3)$

### Zadanie 15

Do etykietowania używamy radixsorta (O(n*d), gdzie d-długość ciągów, n - liczba ciągów).

Najpierw numerujemy n podsłów 1literowych, potem n-2 2-literowych, ..., n-15 16-literowych - za każdym razem łączymy 2 sąsaiednie k-literowe i otrzymujemy k+1 literowe.
31-literowe otrzymujemy łącząć słowo 16-literowe z przesunietym o 15 drugim słowem 16-literowym.

### Zadanie 16
bfs
### Zadanie 17

### Zadanie 18

ciagi znakow traktujemy jako liczby w systemie o podstawie |U|, jesli liczby sie robia zbyt duze to robimy modulo jakies pierwsze q. liczymy liczbe wzorca p i liczbe |P| literowego prefiksu tekstu, porownujemy, jesli sa rowne to musimy sie przejsc literka po literce i sprawdzic, a potem odcinamy pierwsza cyfre tekstowej liczby i dodajemy nastepna.

### Zadanie 19

Każdy wierzchołek nie może stracić max 2 dzieci, dlatego w momencie starty 2 dziecka odcinamy też rodzica. Odcięcie rodzica mogło być odcięciem 2 dziecka dziadka, wtedy dziadka też trzeba odciąć. To się może propagować aż do korzenia.

### Zadanie 20

for i<- n/2,...,1
przesun_nizej(K, i)

## 2019 Poprawka

### Zadanie 1

drzewo zakorzenione w x ma co najmniej n >= 2^bh(x) -1 wierzcholkow, zatem bh(x) <= log(n + 1) a wysokość w takim drzewie jak w zadaniu <= 3bh(x), czyli maksymalna wysokość to 3log(n + 1), gdzie n - #wierzchołków wewnętrznych.

### Zadanie 2

T(n) = T(sufit(n/3)) + T(2n/3)+ O(n)
O(nlogn)

### Zadanie 3

- 1 -> n^2/3 jest O(n) wiec zalezy co dalej
- log n -> O(n)
- n^1/3 * n^2/3 O(n)
- n^4/3 to juz nie jest! losujemy nowa

### Zadanie 4

for i in 1...n
    mini = i
    for j in i...n
        if (T[mini] > T[j])
            mini = j
    swap(T[i], mini)

### Zadanie 5
Porównujemy a_i z a_i+1 (i=1,3,5,..), mniejszy trafia do zbioru mini, większy do maxi. SZukamy liniowo maxa w maxi i mina w mini, jeśli n nieparzyste to porównujemy min i max z a_n.

sufit(3/2n)-2 porównań

### Zadanie 6
sufit(log (n - k)) - może znależć się na dowolnej wysokości h, o ile istnieje 2^h - 1 większych od niego (zakładamy, że mamy pełny kopiec) (i h < log n - 1, bo kopiec ma wysokosc log n)

### Zadanie 7
O(loglogn)

succ(V, x)
    if (V.max < x)
        ret inf
    if (V.min > x) 
        ret V.min
    i = hogh(x)
    if v.clus[i].max > x
        j = succ(clus[i], liw(x))
    else
        i = succ(sum, i)
        j = v.clus[i].min
    ret index(i, j)

### Zadanie 8
8 pierwiastków 8-stopnia, 16 16-stego

### Zadanie 10

find splayu(x) przeczytaj korzen
insert splayu(x) odcinamy mu lewe poddrzewo, i przyczepiamy je x-owi a potem go przyczepiamy jako prawe
delete splayu(x) i splayu(inf) na lewym poddrzewie L, wtedy na pewno jego korzen ma jedno dziecko a drugiego nie wiec mozna mu wsadzic P na prawe poddrzewo

### Zadanie 11

$E = suma(suma(1/m))=(n po 2)/m=50 \cdot 49/(2m) \\
50*49/(2m) = 10 \\
m = 5*49/2=122,5$
czyli nie ma dziekuje bardzo prosze mi dac maxa

### Zadanie 12
W obu może być n pojedynczych wierzchołków.

### Zadanie 13

w metodzie liniowej
_234_ ___9_
w kwadratowej tez ale za trudne

### Zadanie 14

$\Theta(log n)$ scalające

### Zadanie 15

zwykły quicksort

### Zadanie 16

minimalnie 3 (1 spójna składowa i 2 wierzchołki), maksymalnie 4 (3 pojedyncza wierzchołki i 1 składowa, 1 krawędź odrzucona, bo cykl)

### Zadanie 17
F(1)=1
F(i)=2^F(i)

maksymalnie w grupie i : F(i)-F(i-1) rzędów

### Zadanie 18w
aaaaaaaabc

### Zadanie 19

### Zadanie 20
P : aaaaaaa
T : aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa

:::spoiler Poprawka 2015
1. Opisz ideę algorytmu znajdowania mediny opartego na idei próbkowania losowego

Losujemy $n^{3/4}$ elementów z początkowego zbioru S powtórzeniami do zbioru R. Wyznaczamy $x = kn^{-1/4}, l = max(1, x - podloga(sqrt(n))), h = min(n^{3/4}, x + podloga(sqrt(n)))$.
$P = {y \in S | R[l] < y < R[h]}$
sprawdzamy czy k \in P (liczymy elementy z S mniejsze od R[l]) i czy |P| < 4 n^{3/4} + 2, jesli tak to sortujemy P i znajdujemy k, wpp. powtarzamy zabawę.

3. Dlaczego Shift-And stosowany jest tylko do krótkich wzorców

Używa operacji shift i and które są szybkie na słowach maszynowych.

4. Lemat zero-jedynkowy i idea dowodu

Jeśli sieć sortuje wszystkie ciągi zero-jedynkowe to sortuje wszystkie ciągi.

Lemat: jeśli sieć dla ciągu a daje b to dla f niemalejacej i ciagu f(a) da f(b).

Nie wprost zalozmy ze jest para ai < aj w zlej kolejnosci w ciagu wynikowym, niech f(x) = (x < aj). Siec sortuje 0-1 dobrze wiec sprzecznosc.

5. Jakiej struktury danych użyjesz do implementacji kolejki priorytetowej dla zbioru kluczy {0...n}, gdzie operacje kolejkowe są w O(lglgn). Opisz ideę jej konstrukcji.

emde boas. mamy tablice ktora dla kazdego elementu uniwersum pamieta czy jest w kolejce (t[element] = 0 lub 1). Podzielmy tablice na mniejsze grupki (cluster) długosci sqrt(n) (jest ich sqrt(n)). Dla kazdej grupki przechowujemy informacje czy jest niepusta (w streszczeniu). Grupki i streszczenia to tez struktury emde boasa, stuktura jest rekurencyjna (streszczenia maja swoje streszczenia).
Zeby operacja nastepnika wymagala jednego wywolania rekurencyjnego bedziemy przechowywac minimum i maksimum w kazdej strukturze, sprawdzamy czy dany element x jest mniejszy od maksimum zeby wiedziec czy szukac go w jego clusterze, jesli on jest maksimum to nastepnikiem jest najmniejszy element nastepnego niepustego clustera, czyli wolamy nastepnik(strzeszczenie, x), nastepnikiem jest min wyniku.
Zeby operacja insert byla szybka minimum jest leniwe, nie zapisujemy go rekurencyjnie.

6. Rozważmy słownik statyczny realizowany przy pomocy haszowania dwupoziomowego. Załóżmy, że pierwotna funkcja haszująca w k-tym kubełku umieszcza n elementów. Jaki jest rozmiar tablicy wtórnej w której będą te elementy umieszczane. Wyjaśnij dlaczego rozmiar jest taki a nie inny.

n^2, losujemy druga funkcje az bedzie bezkolizyjna i nie chcemy sie przy tym napracowac, wiec wybieramy rozmiar który daje mala liczbe oczekiwana losowan (< 2).

7. Idea sprawdzania izomorfizmu drzew. Czas działania

Dla obu drzew robimy to samo:
Rozwazamy warstwy drzewa od najwyzszej, warstwa wierzcholka jest jego wysokosc.
Na h-tej warstwie wszystkim wierzcholkom dajemy ta sama etykiete.
Na i-tej warstwie dla kazdego wierzcholka tworzymy liste jego poddrzew z etykiet z poprzedniej warstwy. listy sortujemy leksykograficznie (radix sort), zeby nadac im nowe etykiety.
Sprawdzamy czy nowe listy etykiet sie zgadzaja na obu drzewach, jesli tak przechodzimy do nastepnej warstwy.

8. W jakim czasie można wykonać ciąg operacji union i find w którym wszystkie opracje union poprzedzają find. Odpowiedź uzasadnij (z tego co pamiętam, to było dopowiedziane, że find jest robiony z kompresją ścieżek).

O(n), kazda operacja union zostawia jedna jednostke podpinanemu wierzcholkowi, find bedzie je zjadac.

9. Który drzewiec określony jest jednoznacznie:
a) wszystkie klucze różne, ale istnieje para równych priorytetów
b) wszystkie priorytety różne, ale istnieje para równych kluczy
c) wszystkie klucze i priorytety są różne

bc

10. Jak można pogodzić istnienie dolnej granicy Omega(nlogn) na sortowanie ciągu n liczb z tym, że counting sort wykonuje mniej niz nlogn operacji.

Ta dolna granica obowiazuje tylko dla modelu zakladajacego same porownania, a counting sort uzywa danych jako indeksow tablicy.

11. Definicja i przykład uniwersalnej rodziny f-cji haszujących

$$\forall_{x,y\in U, x \neq y} |\{h\in H: h(x)=h(y)\}|\le\frac{|H|}{m}$$
((ax + b)mod p) mod m

12. Idea algorytmu plecakowego z powtórzeniami. Przedstaw pseudowielomianowy algorytm. Dlaczego jest on pseudowielomianowy.

Dla kazdej pojemnosci plecaka 0 < i < w, liczymy najlepsza wartosc plecak[i] = max(plecak[i - objetosc przedmiotu] + wartosc przedmiotu) sprawdzajac wszystkie mozliwe przedmioty. zlozonosc to O(wn), czyli zalezy nie tylko od n.

13. FFT jest dziel i zwyciężaj. Na czym polega redukcja?

Chcemy przeksztalcic wielomian P = a0 + a1x + ... + anx^n na postac punktowa.
P = A(x^2) + xB(x^2)
A = a0 + a2x + ... an x^{n/2}
B = b1 + b3x + ... bn-1 x^{n/2}

Trzeba jeszcze znalezc taki zbior punktow X, zeby po skwadraceniu zostala polowa punktow (rekurencyjnie). Wezmiemy pierwiastki z 1 ntego stopnia.

14. Niech H będzie kopcem dwumianowym (eager) zawierającym 1000000 elementów. Ile najmniej elementów musi zawierać kopiec dwumianowy G, tak aby po połączeniu G z H wynikowy kopiec zawierał:
a) 1 drzewo
b) 2 drzewa
c) 19 drzew

Znajdujemy najmniejsze k takie ze 2^k > 1000000 (1024*1024).
a) 2^k - 1000000 (48576)
b) a + 1 = 48577
c) trzeba dodac brakujace 48575 zeby miec wszystkie pierwsze 19.

15. Pseudokod szybkiej budowy kopca. Jaki jest czas działania.

for i = n/2 down to 2
przesun nizej(K, i)

16. Załóżmy, że przełączniki w sieci ustawione są losowo. Dla jakich n istnieje sieć przełączników o n wejściach która z jednakowym prawdopodobieństwem wygeneruje każdą permutację n elementową. Uzasadnij

2^n

17. Na czym polega kaskadowe odcinanie w kopcach fibonacciego

jesli wszystkie wierzcholki na sciezce x do korzenia stracily juz jakiegos syna a my odetniemy x to kazde z nich po kolei straci drugiego syna i zostanie odcieta.

18. Przykład danych dla których Dijkstra da niepoprawny wynik

ujemne wagi:

19. Który algorytm sortowania w najgorszym wypadku robi cn^2 porównań:
a) quicksort +
b) mergesort -
c) selectsort +
d) insertsort +
e) heapsort -

20. Przedstaw w jaki sposób sieci półczyszczące są wykorzystywane w konstrukcji bitonicznych sieci sortujących.

Siec polczyszczaca dostaje na wejscie dwa ciagi bitoniczne i zwraca jeden czysty a drugi bitoniczny. mozna ustwic rekurencyjnie sieci polczyszczace zeby dostac siec bitoniczna ktora umie sortowac.
Jesli na wejsciu dostaniemy dwie sieci posortowane to mozemy ta dolna wywrocic do gory nogami i mamy ciag bitoniczny na wejsciu ktory mozemy potraktowac siecia bitoniczna.
mozemy teraz druty polaczyc w dwojki, posortowac, dwojki w czworki posortowac ... n/2 w n i mamy posortowane.

któreś: Załóżmy, że przełączniki w sieci ustawione są losowo. Dla jakich n istnieje sieć przełączników o n wejściach która z jednakowym prawdopodobieństwem wygeneruje każdą permutację n elementową.
uogólnione sieci benesa waksmana dla kazdego n.
:::

# Część 2

## 2016
### Zadanie 1
LIS, ale dla kazdej dlugosci pamietamy 2 najmniejsze leksykograficznie podciagi spełniające te własnosci (w normalnej wersji 1)

D-d: :(

### Zadanie 2
Zauważmy, że 1,2,..,n to kolejność topologiczna, zatem możemy przetwarzać wierzchołki w tej kolejnośći.

1) zachłan jest zły 1->2->n
1->3->4->...->n
2) Każdy wierzchołek pamięta maksymalną długość ścieżki z v_1 do siebie (w liczbie wierzchołków)
d[v_1] ustawiamy na 1, pozostałe wierzchołki na 0

Przechodzimy przez wierzchołki w kolejnośći topologicznej : 1,2,..,n.
Dla każdego dziecka 'u' rozważanego wierzchołka 'v' (jeżeli d[v] != 0, wpp. nie rób nic):
d[u] = max(d[u], d[v] + 1)

Zwróć d[v_n] - 1.

Koszt : O(m + n) = O(m).

Poprawność :

3) Grafy ważone:
d[v_1] - oznacza teraz sumę wag krawedzi na drodze (+ brzydkie 1, żeby nie brać wierzchołków spoza sćiezki v_1-v_n).
To d[u] = max(d[u], d[v] + 1) zmieniamy na d[u] = max(d[u], d[v] + 1).
Zwracamy d[v_n] - 1.

## 2019
### Zadanie 1
### Zadanie 2

jak na wykladzie tylko dodajemy do tablicy glebokosc i jak liczymy nowa wartosc to bierzemy z minimum glebokosci.

### Zadanie 3

a) problem rownowazny z poprawnym nawiasowaniem wiec rozw to liczby catalana

b) tak jak zawsze n^3

## 2021
### Zadanie 1
### Zadanie 2

### Zadanie 3
Szukanie najmniejszej odległości między parą punktów z wykładu (dziel i zwyciężaj, każda część zwróci najmniejsza i druga najmniejsza odleglosc), tylko w pasku przy szukaniu najmniejszego pamiętamy 2 najmniejsze i porównujemy z tymi z lewej i prawej połówki.

## 2022
### Zadanie 1
Ułóż algorytm rozwiązujący problem znajdowania najbliżej położonej pary punktów na płaszczyźnie oparty na następującej idei:
Niech d będzie odległością pomiędzy parą najbliżej położonych punktów spośród punktów $p_1, p_2, \dots, p_{i-1}$. Sprawdzamy, czy $p_i$ leży w odległości mniejszej niż $d$ od któregoś z poprzednich punktów. W tym celu dzielimy płaszczyznę na odpowiednio małe kwadraty tak, by w każdym z nich znajdował się nie więcej niż jeden punkt. Te "zajęte" kwadraty pamiętamy w słowniku.
Twój algorytm powinien działać w oczekiwanym czasie liniowym. Jeśli nie potrafisz zbudować algorytmu opartego na powyższej idei, możesz opracować algorytm na innej (ale spełniający te same wymagania czasowe).

### Zadanie 2
Ułóż algorytm, który dla danych ciągów $x$ i $y$ znajduje ich najdłuższy wspólny podciąg zawierający słowo "abba" jako swoje podsłowo.
Uwaga: nie pomyl pojęć podsłowo i podciąg.

### Zadanie 3
Przeprowadź analizę zamortyzowanego kosztu ciągu operacji "insert", "deletemin", "decreasekey", "meld", "findmin" wykorzystywanych na kopcach Fibonacciego, w których kaskadowe wykonania operacji "cut" wykorzystywane jest dopiero wtedy, gdy wierzchołek traci trzeciego syna.

Każde drzewo ma 1j.k. i każdy wierzchołek ma tyle j.k. ilu stracił synów (o ile sam nie został odcięty).
- findmin - O(1), mamy wskaźnik MIN
- meld - O(1), złączenie list i aktualizacja MINa
- decreaskey(x) - ma do dyspozycji 2 j.k, 1 na nieskopoziomowe, drugą dla rodzica x (jeśli x został odcięty); jeśli rodzic xa utracił 3-syna, to ma 3j.k., 1 na niskopoziomowe, 1 j.k. daje swojemu rodzicowi a 1 zostawia dla siebie - po cut staje się nowym drzewem, więc potrzebuje j.k. Dalej na ścieżce analogicznie.
- insert - O(1), nowy wierzchołek wstawiany na listę, dostaje
- deletemin - O(logn), ususwamy mina, jego dzieci wrzucamy na listę; trzeba złączyć wszystkie drzewa tego samego rzędu - drzewa które wcześniej były na liście mogą opłacić przyłączenie z własnej kieszeni, dzieci zmarłego mina nie - potrzebujemy dla nich dodatkowych jednostek.
Rząd drzewa <= log n.

Lemat: *Dla każdego wierzchołka o rzędzie k, drzewo zakorzenione w x ma rozmiar wykładniczy względem k.*

Dowód: Niech $x$ będzie dowolnym wierzchołkiem kopca i niech $y_1, ..., y_k$ będą jego synami uporządkowanymi w kolejności przyłączania. W momencie przyłaczania $y_i$ do $x$-a x miał co najmniej $i-1$ synów (mógł mieć więcej i oni mogli zostać odcięci). Stąd $y_i$ też miał co najmniej $i-1$ synów, ponieważ przyłączamy kopce tego samego rzędu. Od tego momentu mógł stracić najwyżej dwóch synów (bo w p. p. zostałby odcięty). W każdym momencie $i$-ty syn każdego wierzchołka ma rząd co najmniej $i-3$.

Oznaczamy przez $C_i$ najmniejsze drzewo o rzędzie i, spełniające powyższą zależność.
Indukcyjnie:
$C_i$ składa się z korzenia i poddrzew $C_0, C_0 ,C_0, C_1, ..., C_{i-2}$. Liczba wierzchołków $C_i$ ($|C_i|$) jest nie mniejsza niż $2+ \sum^{i-2}_{j=0} |C_j|$, czyli $i$-tej liczbie krów Narayana :cow:. Równanie charakterystyczne: $x^3-x^2-1 = 0$. Liczba wierzchołków jest nie mniejsza niż $1.46557^k$.

Stopień wierzchołków drzew w zmodyfikowanym kopcu Fibonacciego jest ograniczony przez $O(log (n))$.

## 2018 Poprawka
### Zadanie 1
### Zadanie 2
### Zadanie 3

## 2019 Poprawka
### Zadanie 1
### Zadanie 2
### Zadanie 3