<div style="display: flex; flex-direction: column; align-items: center; justify-items: space-between;"> <center> <h1>Geometric Deep Learning for Inverse Graphics</h1> </center> <div style="display: flex; flex-direction: row; justify-items: space-between; align-items: flex-start; height: 100%"> <img src="https://cdn.skoltech.ru/img/logo.png" /> <div style="width: 100%; height: 100%; text-align: right"> Student: Serge Kozlukov<br/> Supervisor: Vladimir Spokoiny<br/> Supervisor: Dmitry Ulyanov </div> </div> <div style="width: 100%; text-align: center;"> May, 2020 </div> </div> <!-- slides: https://hackmd.io/@newkozlukov/msc-predefense-retake --> Note: I should say in advance that not all of the problems discussed on my pre-defense have been fixed. I still haven't prepared fancy pictures, but I will have them on my defense, if one is ever allowed. I'm also yet to switch to standard Skoltech template. My supervisors are Vladimir Spokoiny and Dmitry Ulyanov, and my thesis is about "geometric deep learning for inverse graphics". --- # Background - Hyperbolic DL (hyperbolicdeeplearning.com) - Equivariant CNNs (Cohen/Welling) - Graph convolutional models (e.g. Kipf) Note: In this presentation I should mention three branches of "geometric methods" relevant to my work, namely: - Hyperbolic deep learning, which attempts to exploit something called "curvature". - Equivariant convolutional networks, which like classic convolutions treat inputs as equivalent up to certain transformations. - Graph convolutional networks, which operate on irregular data like graphs and even point clouds --- # NPC spaces  Note: First direction we consider is "hyperbolic deep learning" and for that we need to define what a "hyperbolic space". First of all, a hyperbolic space is a metric space, but very special one. Specifically, metric space is called hyperbolic if it has constant negative _curvature_. A simpler related concept of non-positive curvature can be described in terms of compairson triangles. In your metric space, consider three points $p, q, r$ in a small neighbourhood. Connected by geodesics, they form a triangle with sides $|pq|$, $|qr|$, and $|rp|$. One could construct a unique Euclidean triangle with same sides. Next, one could measure how distance from base point $p$ to the midpoint $\gamma_t$ between $p$ and $q$ compares to its Euclidean analogue. In hyperbolic space the midpoint will appear closer than Euclidean prediction suggests, and on a (positively-curved) sphere the opposite inequality is true. One could also measure sums of angles -- in hyperbolic space they are strictly less than $\pi$, or how volume of a ball grows with its radius -- in hyperbolic space it is exponential. An important observation is that spaces of different constant curvature cannot be isometric --- <!--  -->  A metric tree is an example of hyperbolic space Note: A motivating example of a NPC space is a binary tree. Consider a full binary tree. It is naturally a metric space, whose points are nodes of the tree, and distance is measured in number of edges between nodes. - Originally for graph-like data - Possible "implicit hierarchicities" outside graph data? - **2019:** MiniImagenet classifiers are trying learn a negatively-curved distance ("hyperbolic image embeddings") -- I'll make a slide on that later ---  Stack-able neural layers for hyperbolic embeddings? <small>(Kochurov, Karimov, Kozlukov, Taktasheva, Mazur)</small> Note: ... Model had a number of drawbacks, including significant overfitting and conceptual inconsistencies. 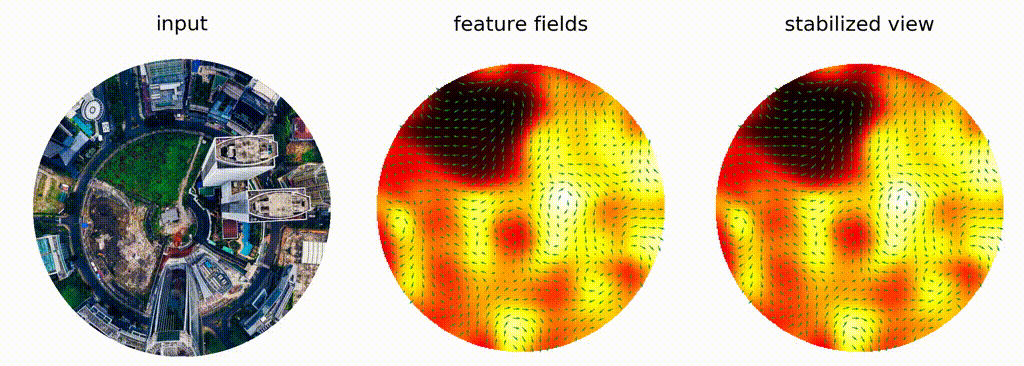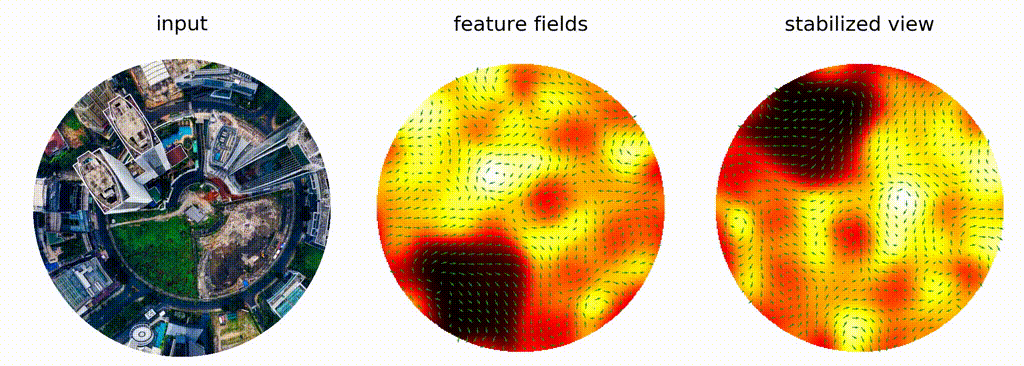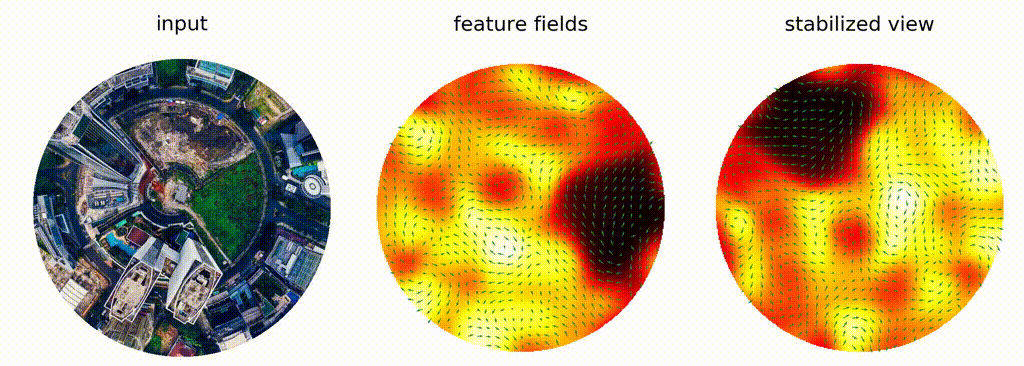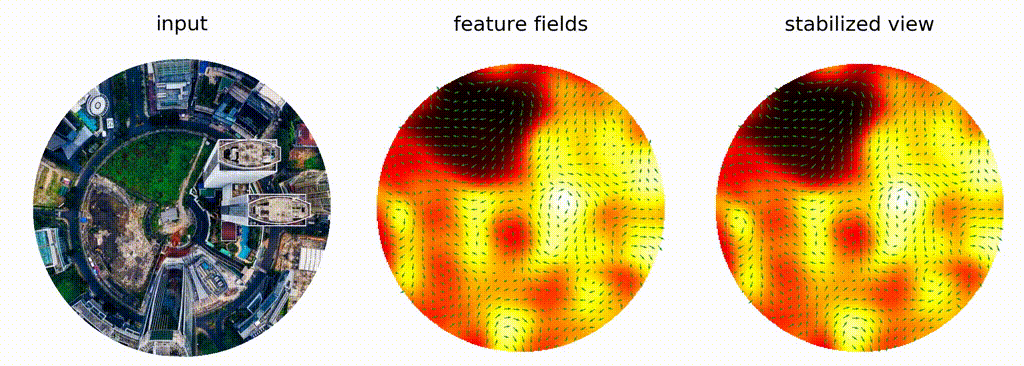I will come back to that later in presentation --- $f*h = x\mapsto \int_G f(g e) h(g^{-1}x)\operatorname{d}g$ E.g. $G=\mathbb{R}^n,$ $e = 0,$ $gx = g + x$ Cohen, Welling, Weiler, ...: **equivariance**  Note: Another branch of geometric methods is development of so-called equivariant neural networks. The success of classic CNNs is understood to be due to pattern-matching behaviour possible because (the usual) convolution commutes with translations: if doesn't matter if you translate an image before or after convolution. That's called equivariance. For certain applications equivariance wrt other transformation groups, e.g. rotations, is desired. Turns out, convolutions can be generalized to arbitrary transformation groups: the illuminating insight is that integral in classic convolution isn't over the domain of a function, but over the group of translations that acts on the domain, and one could pick a different group of transformations, e.g. rotations. Here's visualization from the work of Maurice Weiler and Gabriel Cesa, where they show that features their model generates for rotations of the same image are independent of rotation. That would not be the case for a classic CNN --- - Meanwhile: Deep Learning on Graphs. - E.g. EdgeConv: "and pointclouds too". Dynamic $k$-NN graph, aggregation over direct neighbours Note: One last direction we should mention is the methods that work directly with graphs and pointclouds. I'm sorry it wasn't enough time to prepare an illuminating picture here, but you rememeber the idea from my previous reports and I'll improve this on next iteration --- ## Aim - Stack-able neural layers for hyperbolic embeddings? --- ## Healing H-Conv <table> <tr> <td> - H-Conv 0.1 </td> <td> $\textrm{message} = \log_0 x$ </td> </tr> <tr> <td style="vertical-align: top"> - H-Conv 0.2 - "Relative directions" - Invariance wrt location </td> <td style="width: 5%;"> $\textrm{message} = \log_{x_0} x$ <img src="https://i.imgur.com/leoZN2B.png" width="100%"/> </td> </tr> </table> Note: $x_0$ is one of the points in the sliding window, a "pivot" relative directions blah blah blah, also note how this is in tone with Cohen's works on equivariance, but not quite --- ## Hyperbolic EdgeConv - EdgeConv: $\mathrm{message} = (x_i, x_j - x_i)$ - Riemannian EdgeConv: $\mathrm{message} = (\log_0 x_i, \log_{x_i} x_j)$ - Observation: this is equivalent to H-Conv0.2 (on a regular grid) Note: Second experiment is generalizing the EdgeConv model to manifold-valued embeddings. This amounts to replacing vector subtraction with logarithmic map, and choosing appropriate pooling operation. In fact the way I implement image convolutions now is by re-using generalized EdgeConv, throwing away the $k$-NN graph construction step --- ## Results - H-Conv0.2 and H-EdgeConv "almost gets to the baselines" with much smaller networks and smaller embedding sizes - Modelnet40 classification: .8 acc w/ 85K params vs 1M - There's still room for improvement --- ## Publications (co-author) - geoopt (ELLIS workshop) - Under review: self-supervised depth denoising --- ## Discussion - Hconv2020: "hyperbolic conv" along spatial dimensions? - Need "signal on hyperbolic space" interpretation - Discrete: $\frac{1}{|\mathrm{window}|}\sum_{x\in\mathrm{window}} \delta_x$ - Invariant wrt hyp translations, but the rest of isometries group? --- ## Possible amendments - Replace $\delta_x$'s with a better basis (e.g. spherical harmonics)? - Integrate over all ball-preserving M\"obius transformations, similar to Cohen?