# Time Complexity
**Topics covered :**
1. Log Basics + Iteration Problems
2. Comparing Iterations using Graph
3. Time Complexity - Definition and Notations (Asymptotic Analysis - Big O)
6. TLE
7. Importance of Constraints
:::success
There are a lot of quizzes in this session, please take some time to think about the solution on your own before reading further.....
:::
## Basics of Logarithm
Q. What is the meaning of LOG ?
A. Logarithm is the inverse of exponential function.
Q. How to read the statement "log<sub>b</sub>(a)"?
A. To what value we need to raise b, such that we get a.
If log<sub>b</sub>(a) = c, then it means b<sup>c</sup> = a.
**Examples**
1. log<sub>2</sub>(64) = 6
**How?** 2 raise to the power what is 64? It's 6 since 2<sup>6</sup> = 64
2. log<sub>3</sub>(27) = 3
3. log<sub>5</sub>(25) = 2
4. log<sub>2</sub>(32) = 5
Now, calculate the floor values of the following logarithms.
5. log<sub>2</sub>(10) = 3
6. log<sub>2</sub>(40) = 5
**Note:**
If 2<sup>k</sup> = N => log<sub>2</sub>(N) = k
Let's look at one more formula:
1. What is log<sub>2</sub>(2^6)?
A. 6
Explanation: To what power you should raise 2, such that it equates to 2^6.
2. What is log<sub>3</sub>(3^5)?
A. 5
Explanation: To what power you should raise 3, such that it equates to 3^5.
**Note:**
In general, log<sub>a</sub>(a^N) = N
**Question**:
Given a positive integer N, how many times do we need to divide it by 2 (Consider only integer part) until it reaches 1.
For example, N = 100
100 -> 50 -> 25 -> 12 -> 6 -> 3 -> 1
Hence, 6 times.
What if N = 324?
324 -> 162 -> 81 -> 40 -> 20 -> 10 -> 5 -> 2 -> 1
Hence, 8 times.
### **Question**
How many times we need to divide 9 by 2 till it reaches 1 ?
**Choices**
- [ ] 4
- [x] 3
- [ ] 5
- [ ] 2
**Explanation:**
N --> N/2 --> N/4 --> N/8 --> ...... 1
N/2^0 --> N/2^1 --> N/2^2 --> N/2^3 --> ...... N/2^K
N/2^K = 1
K = log<sub>2</sub>(N)
### **Question**
How many times we need to divide 27 by 2 till reaches 1 ?
**Choices**
- [ ] 5
- [x] 4
- [ ] 3
- [ ] 6 -->
### **Question**
How many iterations will be there in this loop ?
```pseudocode
N > 0
i = N;
while (i > 1) {
i = i / 2;
}
```
**Choices**
- [ ] N
- [ ] N/2
- [ ] sqrt(N)
- [x] log(N)
**Explanation:**
The given loop starts with the initial value of i as N and continues until i becomes less than or equal to 1, by repeatedly dividing i by 2 in each iteration.
Hence, Iterations are log(N)
### **Question**
How many iterations will be there in this loop
```
for(i=1; i<N; i=i*2)
{
...
}
```
**Choices**
- [ ] infinite
- [ ] sqrt(N)
- [ ] 0
- [x] log(N)

### **Question**
How many iterations will be there in this loop ?
```pseudocode
N>=0
for(i=0; i<=N; i = i*2)
{
...
}
```
**Choices**
- [x] Infinite
- [ ] N/2
- [ ] 0
- [ ] log(N)
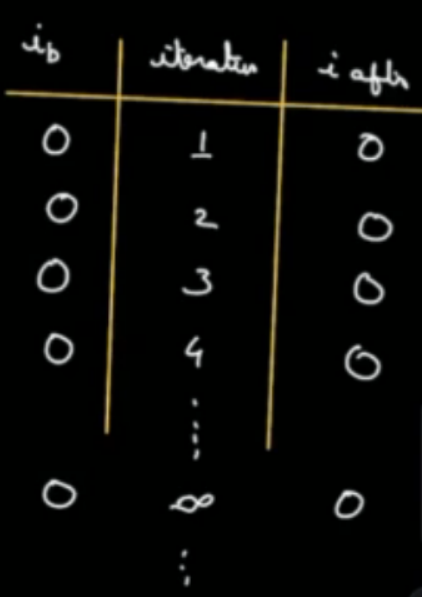
### Question
How many iterations will be there in this loop
```
for(i=1; i<=10; i++){
for(j=1; j<=N; j++){
/ ......../
}
}
```
**Choices**
- [ ] N + N
- [ ] N^2
- [x] 10 * N
- [ ] N + 10
> Multiplying the loops each time might not be correct. In this case, it works.
### **Question**
How many iterations will be there in this loop
```
for(i=1; i<=N; i++){
for(j=1; j<=N; j++){
...
}
}
```
**Choices**
- [ ] 2 * N
- [x] N * N
- [ ] 10 * N
- [ ] N * sqrt(N)
**Explanation:**
The given loop consists of two nested loops. The outer loop iterates from i=1 to i=N, and the inner loop iterates from j=1 to j=N.
For each value of i in the outer loop, the inner loop will iterate N times. This means that for every single iteration of the outer loop, the inner loop will iterate N times.
Therefore, the correct answer is N * N.
### **Question**
How many iterations will be there in this loop
```
for(i=1; i <= N; i++){
for(j=1; j <= N; j = j*2){
...
}
}
```
**Choices**
- [ ] (N^2 + 2N + 1)/2
- [x] N * log(N)
- [ ] N^2
- [ ] N(N+1)/2
**Explanation:**
The given loop consists of two nested loops. The outer loop iterates from i=1 to i <= N, and the inner loop iterates from j=1 to j <= N, with j being incremented by a power of 2 in each iteration.
For each value of i in the outer loop, the inner loop iterates in powers of 2 for j. This means that the inner loop will iterate for j=1, 2, 4, 8,... up to the largest power of 2 less than or equal to N, which is log<sub>2</sub>(N).
Therefore, the correct answer is N * log<sub>2</sub>(N).
### **Question**
How many iterations will be there in this loop ?
```
for(i = 1; i <= 4; i++) {
for(j = 1; j <= i ; j++) {
//print(i+j)
}
}
```
**Choices**
- [ ] log(N)
- [ ] 2N
- [x] 10
- [ ] N -->
### **Question**
How many Iterations will be there in this loop ?
```
for(i = 1; i <= N; i++) {
for(j = 1; j <= i ; j++) {
//print(i+j)
}
}
```
**Choices**
- [ ] log(N)
- [x] N*(N+1)/2
- [ ] (N-1)/2
- [ ] N/2
### **Question**
How many iterations will be there in this loop
```
for(i=1; i<=N; i++){
for(j=1; j<=(2^i); j++)
{
...
}
}
```
**Choices**
- [ ] 2^N
- [x] 2 * (2^N - 1)
- [ ] 2 * (2N)
- [ ] infinite

This is GP, where a=2, r=2 and no. of terms are N.
Consider two algorithms Algo1 and Algo2 given by Kushal and Ishani respectively.
Considering **N** to be the size of the input:
Algo|Number of Iterations
-|-
Algo1|100 * log(N)
Algo2|N / 10
Now, see the graph of the two algorithms based on N.
Graphs info:
* X-axis plots N (input size)
* Red line (Algo 1): **100 * log(N)**
* Blue line (Algo 2): **N/10**

### Observations:
Assuming both graphs intersect at N = 3500, let's draw some observations.
For small input (N <= 3500), Ishani's algorithm performed better.
For large input (N > 3500), Kushal's algorithm performed better.
**In today's world data is huge**
* IndiaVSPak match viewership was **18M**.
* Baby Shark video has **2.8B** views.
Therefore, Kushal's algorithm won since it has lesser iterations for huge data value.
*We use **Asymptotic Analysis** to estimate the performance of an Algorithm when Input is huge.*
**Asymptotic Analysis** OR **Big(O)** simply means analysing perfomance of algorithms for **larger inputs**.
### Calculation of Big(O)
**Steps** for **Big O** calculation are as follows:
* Calculate **Iterations** based on **Input Size**
* Ignore **Lower Order Terms**
* Ignore **Constant Coefficients**
**Example-**
Kushal's algo took **100 * log<sub>2</sub>N** iterations: Big O is **O(log<sub>2</sub>N)**
Ishani's algo took **N / 10** iterations: Big O is **O(N)**
**For example**,
1. Iterations: 4N^2 + 3N + 1
2. Neglect lower order term: 3N + 1; Remaining Term: 4N^2
3. Neglect constant 4
Big O is O(N^2)
### Comparsion Order:
log(N) < sqrt(N) < N < N log(N) < N sqrt(N) < N^2 < N^3 < 2^(N) < N! < N^N
**Using an example**
N = 36
5 < 6 < 36 < 36\*5 < 36\*6 < 36<sup>2</sup> < 36<sup>3</sup> < 2<sup>36</sup> < 36! < 36<sup>36</sup>
**Ques:** What is the big notation time complexity of the following expression?
4N^2 + 3N + 6 sqrt(N) + 9 log_2(N) + 10
Ans = O(N^2)
### Question
F(N) = 4N + 3Nlog(N) + 1
O(F(N)) = ?
**Choices**
- [ ] N
- [x] N * logN
- [ ] Constant
- [ ] N^2
### Question
F(N) = 4NlogN + 3NSqrt(N) + 10^6
O(F(N)) = ?
**Choices**
- [ ] N
- [ ] N * logN
- [ ] N^2
- [x] N * Sqrt(N)
## Why do we neglect Lower Order Terms
Let's say the number of Iterations of an Algorithm are: N<sup>2</sup>+10N
N|Total Iterations = N<sup>2</sup>+10N|Lower Order Term = 10N|% of 10N in total iterations = 10N/(N<sup>2</sup>+10N)*100
-|-|-|-
10|200|100|50%
100|10<sup>4</sup>+10<sup>3</sup>|10<sup>3</sup>|Close to 9%
10000|10<sup>8</sup>+10<sup>5</sup>|10<sup>5</sup>|0.1%
## Conclusion
We can say that, as the **Input Size** increases, the contribution of **Lower Order Terms** decreases.
### Why do we neglect Constant Coefficients
When the comparison is on very larger input sizes, the constants do not matter after a certain point. For example,
| Algo 1(Nikhil)|Algo 2(Pooja)|Winner for Larger Input|
| -------- | -------- | -------- |
| 10 * log<sub>2</sub> N | N | Nikhil |
| 100 * log<sub>2</sub> N | N | Nikhil |
| 9 * N | N<sup>2</sup> | Nikhil |
| 10 * N | N<sup>2</sup> / 10| Nikhil |
| N * log<sub>2</sub> N | 100 * N | Pooja |
## Issues with Big(O)
### Issue 1
**We cannot always say that one algorithm will always be better than the other algorithm.**
**Example:**
* Algo1 (Iterations: 10<sup>3</sup> N) -> Big O: O(N)
* Algo2 (Iterations: N<sup>2</sup>) -> Big O: O(N<sup>2</sup>)
* Algo 1 is better than Algo 2 but only for large inputs, not for small input sizes.
|Input Size (N)| Algo 1 (10<sup>3</sup>) | Algo 2 (N<sup>2</sup>) | Optimised|
| --| --| --| --|
|N = 10| 10<sup>4</sup>| 10<sup>2</sup>|Algo 2|
|N = 100| 10<sup>5</sup>| 10<sup>4</sup>|Algo 2|
|N = 10<sup>3</sup>| 10<sup>6</sup>| 10<sup>6</sup>|Both are same|
|N = 10<sup>3</sup> + 1| (10<sup>3</sup>)*(10<sup>3</sup> + 1)| (10<sup>3</sup> + 1)*(10<sup>3</sup> + 1)|Algo 1|
|N = 10<sup>4</sup>| 10<sup>7</sup>| 10<sup>8</sup>|Algo 1|
**Claim:** For all large inputs >= 1000, Algo 1 will perform better than Algo 2.
### Issue 2
If 2 algorithms have same higher order terms, then Big O is not capable to identify algorithm with higher iterations.
Consider the following questions -
Count the number of odd elements from 1 to N
Code 1: Iterations: N
```pseudocode
for (int i = 1; i <= N; i++) {
if (i % 2 != 0) {
c = c + 1;
}
}
```
Code 2: Iterations: N/2
```pseudocode
for (int i = 1; i <= N; i = i + 2) {
c = c + 1;
}
```
In both, Big O is O(N) but we know second code is better.
## Time Limit Exceeded Error
* **Is it necessary to write the entire code and then test it to determine its correctness?**
* **Can we assess the logic's viability before writing any code?**
### Online Editors and Why TLE occurs
* Codes are executed on online servers of various platforms such as Codechef, Codeforces, etc.
* The **processing speed** of their server machines is **1 GHz** which means they can perform **10<sup>9</sup> instructions** per second.
* Generally, **codes should be executed in 1 second**.
Using this information, we can say at max our code should have at most **10<sup>9</sup> instructions**.
Instructions means any single operation such as multiplication, addition, function calling, single variable declaration, etc.
### Question
Consider the following code:
Find the total number of instructions in the code below (Note that the instructions involved in the loop part are repetitive)

**Conclusion:**
Calculating Instructions is tedious job, rather we can make certain approximations in terms of number of Iterations.
### Approximation 1
Suppose the **code** has as small as **10 Instructions in 1 Iteration**.
Therefore,
| Instructions | Iterations |
| -------- | -------- |
| 10 | 1 |
| 10^9 | 10^8 |
In **1 sec**, we can have at max **10<sup>9</sup> Instructions** or **10<sup>8</sup> Iterations**, provided there are **10 Instructions / Iteration**.
### Approximation 2
Suppose the **code** has as huge as **100 Instructions in 1 Iteration**.
Therefore,
| Instructions | Iterations |
| -------- | -------- |
| 100 | 1 |
| 10^9 | 10^7 |
In **1 sec**, we can have at max **10<sup>9</sup> Instructions** or **10<sup>7</sup> Iterations**, provided there are **100 Instructions / Iteration**.
### Conclusion:
In general, our code can have **10<sup>7</sup>** to **10<sup>8</sup> Iterations** to be able to run in **1 sec**.
## General Structure to solve a question
### How to approach a problem?
* Read the **Question** and **Constraints** carefully.
* Formulate an **Idea** or **Logic**.
* Verify the **Correctness** of the Logic.
* Mentally develop a **Pseudocode** or rough **Idea of Loops**.
* Determine the **Time Complexity** based on the Pseudocode.
* Assess if the time complexity is feasible and won't result in **Time Limit Exceeded (TLE)** errors.
* **Re-evaluate** the **Idea/Logic** if the time constraints are not met; otherwise, proceed.
* **Code** the idea if it is deemed feasible.
### Importance of Constraints
#### Question
If 1 <= N <= 10<sup>5</sup>,
then which of the following Big O will work ?
| Complexity | Iterations | Works ? |
| -------- | -------- | -------- |
| O(N<sup>3</sup>) | (10<sup>5</sup>)<sup>3</sup> | No |
| O(N<sup>2</sup>) log N | (10<sup>10</sup>)*log 10<sup>5</sup> | No |
| O(N<sup>2</sup>) | (10<sup>5</sup>)<sup>2</sup> | No |
| O(N * log N) | (10<sup>5</sup>)*log 10<sup>5</sup> | Yes |
#### Question
If 1 <= N <= 10<sup>6</sup>,
then which of the following Big O will work ?
| Complexity | Iterations | Works ? |
| -------- | -------- | -------- |
| O(N<sup>3</sup>) | (10<sup>6</sup>)<sup>3</sup> | No |
| O(N<sup>2</sup>) log N | (10<sup>12</sup>)*log 10<sup>6</sup> | No |
| O(N<sup>2</sup>) | (10<sup>12</sup>) | No |
| O(N * log N) | (10<sup>6</sup>)*log 10<sup>6</sup> ~ 10<sup>7</sup> | May Be |
| O(N) | (10<sup>6</sup>) | Yes |
#### Question
If constraints are
1 <= N <= 100, N<sup>3</sup> will also pass.
If constraints are
1 <= N <= 20, 2<sup>N</sup> will also pass.
**Note:**
In Online Assessments, if we are not getting any other approach to a problem, try out the code; it may pass some test cases, which is better than nothing.