# Introduction to Problem Solving
---
Notes Description
---
* Introduction to Problem Solving
* Time Complexity
* Introduction to Arrays
* Prefix Sum
* Carry Forward
* Subarrays
* 2D Matrices
* Sorting Basics
* Hashing Basics
* Strings Basics
* Bit Manipulation Basics
* Interview Problems
**Following will be covered in the notes!**
1. Count the Factors
2. Optimisation for counting the Factors
3. Check if a number is Prime
4. Sum of N Natural Numbers
5. Definition of AP & GP
6. How to find the number of a times a piece of code runs, i.e, number of Iterations.
7. How to compare two Algorithms.
## Count of factors of a number N
Q. What is a factor?
A. We say i is a factor of N if i divides N completely, i.e the remainder is 0.
How to programmatically check if i is a factor of N ?
We can use % operator which gives us the remainder.
=> **N % i == 0**
**Question 1:**
Given N, we have to count the factors of N.
**Note:** N > 0
**Question 2:**
Number of factors of the number 24.
**Choices**
- [ ] 4
- [ ] 6
- [x] 8
- [ ] 10
**Explanation:**
1, 2, 3, 4, 6, 8, 12, and 24 are the factors.
**Question 3:**
Number of factors of the number 10.
**Choices**
- [ ] 1
- [ ] 2
- [ ] 3
- [x] 4
**Explanation:**
1, 2, 5, and 10 are the factors.
:::warning
Please take some time to think about the solution approach on your own before reading further.....
:::
### Counting Factors Brute force solution
What is the minimum factor of a number ?
=> 1
What is the maximum factor of a number ?
=> The number itself
So, we can find all factors of N from 1 to N.
### Pseudocode
```cpp
function countfactors (N):
fac_count = 0
for i = 1 till N:
if N % i == 0:
fac = fac + 1
return fac
```
### Observations for Optimised Solution
* Now, your code runs on servers.
* When you submit your code, do you expect some time within which it should return the Output ?
* You wouldn't want to wait when you even don't know how long to wait for ?
* Just like that one friend who says, 'Just a little more time, almost there.' And you feel annoyed, not knowing how much longer you'll have to wait.
Servers have the capability of running ~10^8 Iterations in 1 sec.
|N| Iterations| Execution Time|
|-|----------|---------- |
|10^8| 10^8 iterations| 1 sec |
|10^9| 10^9 iterations| 10 sec |
|10^18| 10^18 iterations| 317 years |
### Optimisation for Counting Factors
**Optimization:**
i * j = N -> {i and j are factors of N}
=> j = N / i -> {i and N / i are factors of N}
For example, N = 24
|i| N / i|
|-|----------|
|1| 24|
|2| 12|
|3| 8|
|4| 6|
|6| 4|
|8| 3|
|12| 2|
|24| 1|
Q. Can we relate these values?
A. We are repeating numbers after a particular point. Here, that point is from 5th row.
Now, repeat the above process again for N = 100.
|i| N / i|
|-|----------|
|1| 100|
|2| 50|
|4| 25|
|5| 20|
|10| 10|
|20| 5|
|25| 4|
|50| 2|
|100| 1|
:::warning
Please take some time to think about the solution approach on your own before reading further.....
:::
The factors are repeating from 6th row. After a certain point factors start repeating, so we need to find a point till we have to iterate.
We need to only iterate till -
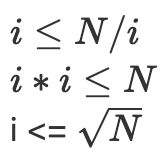
### Pseudocode
```cpp
function countfactors (N):
fac_count = 0
for i = 1 till sqrt(N):
if N % i == 0:
fac = fac + 2
return fac
```
Q. Will the above work in all the cases?
A. No, not for perfect squares. Explain this for N = 100, what mistake we are doing. We will count 10 twice.
**Observation:** Using the above example, we need to modify the code for perfect squares.
### Pseudocode with Edge Case Covered
```cpp
function countfactors (N):
fac_count = 0
for i = 1 till sqrt(N):
if N % i == 0:
if i == N / i:
fac = fac + 1
else:
fac = fac + 2
return fac
```
Dry run the above code for below examples,
N = 24, 100, 1.
|N| Iterations| Execution Time|
|-|----------|---------- |
|10^18| 10^9 iterations| 10 secs |
To implement sqrt(n) , replace the condition i <= sqrt(N) by i * i <= N.
### Follow Up Question
Given N, You need to check if it is prime or not.
**Question**
How many prime numbers are there?
10, 11, 23, 2, 25, 27, 31
**Choices**
- [ ] 1
- [ ] 2
- [ ] 3
- [x] 4
**Explanation:**
Q. What is a prime Number?
A. Number which has only 2 factors, 1 and N itself.
So, 11, 23, 2, and 31 are the only prime numbers since they all have exactly 2 factors.
## Prime Check
Our original question was to check if a number is prime or not. For that, we can just count the number of factors to be 2.
```cpp
function checkPrime(N):
if countfactors(N) == 2:
return true
else:
return false
```
For N = 1, it will return false, which is correct. Since, 1 is neither prime nor composite.
---
**Question**
1 + 2 + 3 + 4 + 5 + 6 + .. 100 = ?
**Choices**
- [ ] 1010
- [x] 5050
- [ ] 5100
- [ ] 1009
**Explanation:**

Generalize this for the first N natural numbers.

## Some basic math properties:
1. `[a,b]` - This type of range means that a and b are both inclusive.
2. `(a,b)` - This type of range means that a and b are both excluded.
**Question**
How many numbers are there in the range [3,10]?
**Choices**
- [ ] 7
- [ ] 6
- [x] 8
- [ ] 10
**Explanation:**
The range [3,10] includes all numbers from 3 to 10, inclusive. Inclusive means that both the lower bound (3) and the upper bound (10) are included in the range. Thus the numbers that are included are 3 4 5 6 7 8 9 10.
**Question**
How many numbers are there in the range [a,b]?
**Choices**
- [ ] b-a
- [x] b-a+1
- [ ] b-a-1
**Explanation:**
To find the number of numbers in a given range, we can subtract the lower bound from the upper bound and then add 1. Mathematically, this can be expressed as:
```
Number of numbers in the range
= Upper bound - Lower bound + 1
```
### What do we mean by Iteration?
The number of times a loop runs, is known as Iteration.
**Question**
How many times will the below loop run ?
```cpp
for(i=1; i<=N; i++)
{
if(i == N) break;
}
```
**Choices**
- [ ] N - 1
- [x] N
- [ ] N + 1
- [ ] log(N)
**Question**
How many iterations will be there in this loop ?
```cpp
for(int i = 0; i <= 100; i++){
s = s + i + i^2;
}
```
**Choices**
- [ ] 100 - 1
- [ ] 100
- [x] 101
- [ ] 0
**Question**
How many iterations will be there in this loop?
```cpp
func(){
for(int i = 1; i <= N; i++){
if(i % 2 == 0){
print(i);
}
}
for(int j = 1; j <= M; j++){
if(j % 2 == 0){
print(j);
}
}
}
```
**Choices**
- [ ] N
- [ ] M
- [ ] N * M
- [x] N + M
**Explanation:**
We are executing loops one after the other. Let's say we buy first 5 apples and then we buy 7 apples, the total apples will be 12, so correct ans is N + M
## Geometric Progression (G.P.)
> **Example for intution:**
```
5 10 20 40 80 ..
```
In these type of series, the common ratio is same. In the given example the common ratio r is
= 10/5
= 20/10
= 40/20
= 80/40
= 2
**Generic Notation:**
a, a * r, a * r^2, ...
### Sum of first N terms of a GP
**Sum of first N terms of GP:**
=
r cannot be equal to 1 because the denominator cannot be zero.
**Note:**
When r is equal to 1, the sum is given by a * n.
## How to compare two algorithms?
**Story**
There was a contest going on to SORT the array and 2 people took part in it (say Gaurav and Shila).
They had to sort the array in ascending order.
arr[5] = {3, 2, 6, 8, 1} -> {1, 2, 3, 6, 8}
Both of them submitted their algorithms and they are being run on the same input.
### Discussion
**Can we use execution time to compare two algorithms?**
Say initially **Algo1** took **15 sec** and **Algo2** took **10sec**.
This implies that **Shila's Algo 1** performed better, but then Gaurav pointed out that he was using **Windows XP** whereas Shila was using **MAC**, hence both were given the same laptops.........

### Conclusion
We can't evaluate algorithm's performance using **execution time** as it depends on a lot of factors like operating system, place of execution, language, etc.
**Question**
How can we compare two algorithms?
Which measure doesn't depend on any factor?
**Answer:** Number of Iterations
**Why?**
* The number of iterations of an algorithm remains the same irrespective of Operating System, place of execution, language, etc.