# Advanced DSA : Tries 1: Trie of Character
---
### Introduction to Trie
### Definition
A trie, also known as a **prefix tree**, is a tree-like data structure used for efficiently storing a dynamic set of strings or keys, usually associated with text. The term "trie" comes from the word "retrieval" because one of its main applications is in searching and retrieving words or strings based on a prefix or a sequence of characters. This data structure organizes strings by their common prefixes and is characterized by nodes that can have multiple children, typically one child for each possible character in the alphabet.
### Example
Here's an example of a trie to store a few words: "cat", "car", "bat", and "ball".
```plaintext
(root)
/ \
c b
/ \
a a
/ \ / \
t r l t
|
l
```
**Explanation:**
* The root node has three children: 'c' and 'b'.
* The first word, "cat", starts with 'c', so we follow the 'c' child.
* The second level has 'a' as a child node, so we follow it.
* The third level has 't' as a child node, and since this is the end of the word, we mark it as an end node.
* Similarly, we insert "car", "bat", and "ball", following the respective paths.
### Practical Applications :
**Spell Checker:**
Spell checker can be implemented to check if a given word exists in a dictionary or a list of valid words.
**1.Trie Creation:**
* Build a Trie data structure where each node represents a character in a word.
* Insert each word from the dictionary into the Trie by creating nodes for each character and marking the last node of each word as the end of a valid word.
**2.Spell Checking:**
* To check the spelling of a word:
* Start at the root of the Trie.
* Traverse the Trie character by character.
* Move to the corresponding child node for each character in the word.
* If you can't find a child node for a character, the word is not in the dictionary, and it's misspelled.
* If you successfully traverse the Trie to the end of the word, and the last node is marked as the end of a valid word, then the word is spelled correctly.
**Time complexity**:
Spell checking with a Trie has a constant and predictable time complexity of **O(m)**, where "m" is the length of the word you're checking. This efficiency is independent of the dictionary's size, making Tries an excellent choice for spell checking, even with large dictionaries.
**Auto-Complete** :
When a user starts typing a word or phrase, you want to suggest possible completions based on what they've typed so far. A trie can be an excellent data structure for implementing this feature efficiently.
Consider the dictionary : "trim", "trie", "play", "try", "plate", "car", "park".
Here's the representation of the trie :
```txt
(root)
/ | \
t c p
/ | / \
r a l a
/ \ | | \
i y r a r
/\ / \ \
m e y t k
\
e
```
This Trie structure allows for efficient autocomplete suggestions for words that share the same prefix. For example:
* If a user types "tri," it quickly find "**trim**" and "**trie**" as autocomplete suggestions.
* If a user types "pl," it provides "**play**" and "**plate**" as suggestions.
* If a user types "ca" it suggests "**car**".
* If a user types "par" it suggests "**park**".
### Pseudocode
```cpp
class Node {
public:
char data; // A character stored in the node
Node* children[26]; // An array of child nodes for each letter of the alphabet
bool is_end_of_word; // A marker to denote if this node marks the end of a word
Node(char ch) {
data = ch;
for (int i = 0; i < 26; i++) {
children[i] = nullptr; // Initialize all child nodes to nullptr
}
is_end_of_word = false; // Initialize the end-of-word marker to false
}
};
```
Adding the `is_end_of_word` marker to a Trie node is like placing a flag to indicate if the current node represents the end of a complete word. This flag helps efficiently identify full words when searching or suggesting words in a Trie, making it handy for tasks like spell checking and autocomplete.
---
### Question
Draw the Trie data structure based on the given words:
`"tree", "try", and "tip"`
What is the total number of nodes present in the structure (including root)?
**Choices**
- [ ] 4
- [x] 8
- [ ] 11
- [ ] 3
**Explanation:**
The answer is 8 nodes.
The initial Structure:
```cpp
root
```
After inserting : tree
```cpp
root
|
t
/
r
/
e
/
e
```
After inserting : try
```cpp
root
|
t
/
r
/ \
e y
/
e
```
After inserting : tip
```cpp
root
|
t
/ \
r i
/ \ \
e y p
/
e
```
The total number of nodes in the Final structure is 8.
---
### Insert in Trie
Inserting a value into a Trie is a fundamental operation in data structures and algorithms. Each node in a Trie represents a single character, and the path from the root of the Trie to a node spells out a prefix of one or more keys. Here's how to insert a value into a Trie:
* Start at the root node of the Trie.
* For each character in the value you want to insert:
a. Check if the current character is already a child of the current node.
b. If it is, move to that child node.
c. If it isn't, create a new node for that character and add it as a child of the current node, then move to the new node.
* Repeat step 2 for each character in the value.
* After inserting all characters, mark the node corresponding to the last character of the value as the end of a word (or key). This step is important for searching and determining if the Trie contains a particular key.
### Pseudocode
```cpp
void insert(string word) {
TrieNode * current = root;
for (char c : word) {
if (current -> children.find(c) == current -> children.end()) {
current -> children[c] = new TrieNode();
}
current = current -> children[c];
}
current -> isEndOfWord = true;
}
```
---
### Question
In a Trie, during the insertion of a word, what does each node typically represent?
**Choices**
- [x] A character in the word.
- [ ] A whole word.
- [ ] A sentence.
- [ ] A phrase.
---
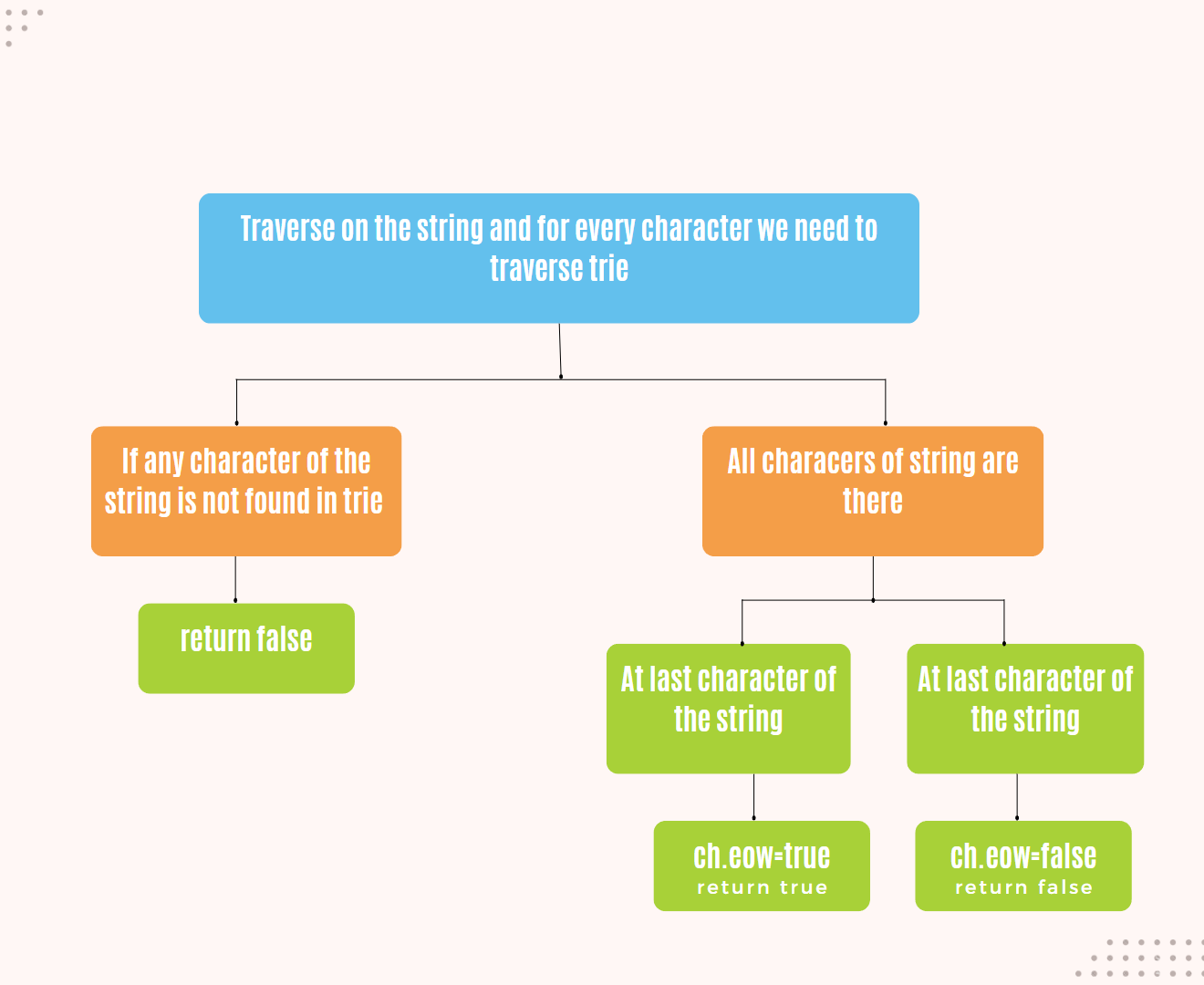
### Search in Trie
Searching for a word in a Trie involves traversing the Trie starting from the root and following the path that corresponds to the characters in the word.
### Pseudocode
```cpp
bool search(string word) {
TrieNode * current = root;
for (char c : word) {
int idx = c - 'a';
if (current -> children[idx] == nullptr) {
return false; // Character not found
}
current = current -> children[idx];
}
return current -> isEndOfWord; // Check if it's the end of a word
}
};
```
**Explanation**:
1. Start at the root of the Trie.
2. For each character in the input word:
* Calculate the index (idx) corresponding to the character.
* If the child node at idx is nullptr, return false.
* Otherwise, update current to the child node at idx.
3. After processing all characters:
* Return true if current marks the end of a word.
* Return false otherwise.
---
### Deletion in Trie
Deletion in a Trie data structure involves removing a specific key (usually a word or a sequence of characters) from the Trie. The goal of deletion is to ensure that the key is no longer present in the Trie. Here's a general approach to delete a value from a Trie:
* Start at the root node of the Trie.
* Traverse the Trie to find the node that corresponds to the value you want to delete. Keep track of the nodes you visit and the characters in the value.
* If you can't find the value, it's not present in the Trie, so there's nothing to delete.
* If you find the node corresponding to the value:
a. Mark the `isEndOfWord` flag of the corresponding node as false to indicate that it's no longer the end of a word.
b. If the node has no other children nodes (i.e., it's not a part of other words), you can safely remove the node and its parent node's reference to it.
c. Continue this process moving upwards in the Trie, checking if each node can be removed.
### Pseudocode
```cpp
void deleteNode(string word) {
TrieNode * current = root;
TrieNode * temp = nullptr;
for (int i = 0; i < word.length(); i++) {
int count = 0;
// Count non-null children
for (char j = 'a'; j <= 'z'; j++) {
if (current -> children.find(j) != current -> children.end()) {
count++;
}
}
// Check if more than one child or current node is end of another word
if (count > 1 || current -> isEndOfWord) {
temp = current;
}
char nc = word[i];
int idx = nc - 'a';
current = current -> children[idx];
current -> isEndOfWord = false;
}
int count = 0;
// Count non-null children
for (char j = 'a'; j <= 'z'; j++) {
if (current -> children.find(j) != current -> children.end()) {
count++;
}
}
if (count > 0) {
return;
} else {
temp -> children[word.back() - 'a'] = nullptr;
}
}
};
```
**Explanation**:
1. The code initializes `current` as the root and `temp` as `nullptr` to keep track of the parent node.
2. It iterates through each character in the `word` to be deleted, just like in the previous version.
3. Inside the loop, it calculates the character index `idx` and character `nc` as before.
4. It checks the same conditions for potential node deletion: more than one non-null child or `current` being the end of another word.
5. It then updates `current` to the next node and marks it as not the end of a word.
6. After the loop, it directly checks if `current` has no non-null children (`current->children.size() == 0`). If this condition is met, it erases the corresponding child node from the parent temp.
---
### Question
What is the purpose of the `isEndOfWord` flag in Trie nodes during deletion?
**Choices**
- [ ] It marks the root node of the Trie.
- [ ] It indicates the presence of an incomplete word.
- [ ] It speeds up the deletion process.
- [x] It signifies the end of a valid word.
---
### Problem 1 Shortest Unique Prefix
Finding the shortest unique prefix in a Trie for a given word or set of words involves traversing the Trie to identify the point where the given word or words diverge from other words in the Trie.
### Observation
Search for each word in the Trie character by character, and stop when you encounter a character node with a frequency of 1. The prefix built up to that point is the shortest unique prefix for the word.
### Example
Let's consider a simple example with a Trie containing the words "tri", "trap", "plate", "cat", "part", "place" and "tie"
Here is the Trie structure for the given words.
<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/065/640/original/trie.png?1708289286" alt="Trie diagram" width=700 />
To understand the shortest unique prefix better, lets take some examples on the given words,
**Find the Shorest Unique Prefix For "trap":**
Lets check the prefix strings one by one, "t", "tr", "tra", "trap"
"t" is a prefix for "tri", "tie" and "trap". So this is not a unique shortest prefix.
"tr" is a prefix for "tri", "trap". So this is not a unique shortest prefix.
"tra" is a prefix for "trap". Thus, **"tra" is a unique shortest prefix.**
---
### Question
What is the shortest unique prefix for **"part"** ?
<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/065/641/original/trie2.png?1708291088" width=700/>
**Choices**
- [ ] p
- [x] pa
- [ ] par
- [ ] part
---
### Observation
Here we are closing working upon the frequency of each character on trie, which helps in finding the unique prefix for a particular word. So lets build a Trie, with frequencies.
Here, the numberic value tells the occurrence of the character.
<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/065/641/original/trie2.png?1708291088" width=700/>
Now, you can find the shortest unique prefixes for the given words as follows:
1.**Word: "cat"**
* Start at the root.
* The first character 'c' appears only once in the Trie (frequency 1).
* Move to the 'a' node.
* The second character 'a' appears only once in the Trie (frequency 1).
* Stop here. The shortest unique prefix for "cat" is "cat" because both 'c' and 'a' occur only once in the Trie.
2.**Word: "place"**
* Start at the root.
* The first character 'p' appears multiple times in the Trie (frequency 2).
* Move to the 'l' node.
* The second character 'l' appears only once in the Trie (frequency 1).
* Move to the 'a' node.
* The third character 'a' appears only once in the Trie (frequency 1).
* Stop here. The shortest unique prefix for "place" is "plac" because 'p', 'l', and 'a' are unique at this point.
**3.Word: "trie"**
* Start at the root.
* The first character 't' appears multiple times in the Trie (frequency 2).
* Move to the 'r' node.
* The second character 'r' appears multiple times in the Trie (frequency 2).
* Move to the 'i' node.
* The third character 'i' appears multiple times in the Trie (frequency 2).
* Stop here. The shortest unique prefix for "trie" is "trie" because 't', 'r', and 'i' are all unique at this point.
Similarly, you can find the shortest unique prefixes for other words as well.