---
tags: 你所不知道的 C 語言, 進階電腦系統理論與實作, NCKU Linux Kernel Internals, 作業系統
---
# 函式呼叫、遞迴呼叫
contributed by <`RusselCK` >
###### tags: `RusselCK`
## [函式呼叫篇](https://hackmd.io/@sysprog/c-function?type=view)
* [History of C](http://en.cppreference.com/w/c/language/history)
* C 語言不允許 nested function
* function 和 data 一樣在 function 內部定義
* nested function 是編譯器的擴展
* 簡化了 C 編譯器的設計
* ==C 語言所有的 function 在語法層面都是位於最頂層 (top-level)==
* callback function
- [數學定義的 Function](https://www.cs.colorado.edu/~srirams/courses/csci2824-spr14/functionsCompositionAndInverse-17.html)
#### Process 和 C 程式的關聯
:::success
背景知識:
1. IRQ (interrupt request)
2. ISR (Interrupt Service Routines)
3. IRQ mode
4. [MMIO (memory mapped I/O) v.s PMIO](https://www.itread01.com/content/1508402471.html)
以網路卡的流程為例:
* 封包進來 -> interrupt -> ISR -> IRQ mode -> 下圖綠色的區塊裡面 (IORQ) 進行記憶體操作(讀取/寫入資料)
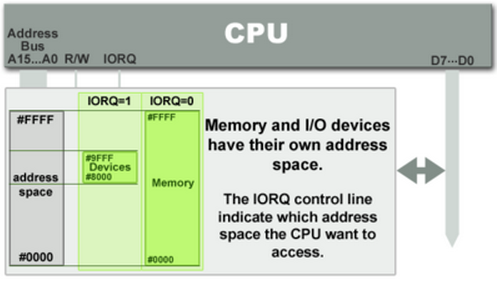
:::
* runtime = 執行時期
- [ ] [The Internals of "Hello World" Program](http://www.slideshare.net/jserv/helloworld-internals)

* bus

* PCI bus : 高速 ( 越靠近 CPU 越快 )
* ISA bus : 低速




* 程式 不會 直接接觸 Memory
* MMU
* Virtual address 轉 Physical address

* 保護 資源

* 寫、讀、執行

* Prepocessing、Compiling、Assembling、Linking

* Relocation

* Symbol

* Symbol 對應到 Virtual address


* 如何把程式載下來?


* Loader
* 從 磁碟( or 網路) 載入到 記憶體

* AS : Address Space
* .text : 存放 機械碼 ( 對應有效的 CPU 指令 )
* 透過 loader 載入到 記憶體
- program break : 虚拟内存中数据段的结束位置


* 參考 動態連結篇 筆記
- function call 會佔用 stack 區域 ( FILO )

* Return address ( 有去有回 )
* Arguments, Local variable, Return address
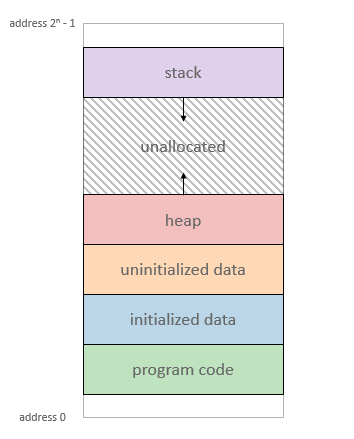
* instructions: 自 object file (ELF) 映射 (map) 到 process 的 program code (機械碼)
* static data: 靜態初始化的變數
* BSS: 全名已 ==不可考==,一般認定為 "Block Started by Symbol”,未初始化的變數或資料
* 可用 `size` 指令來觀察
* Heap 或 data segment: 執行時期才動態配置的空間
* sbrk 系統呼叫 (sbrk = set break)
* malloc/free 實際的實做透過 sbrk 系統呼叫
* [虚拟内存探究-- 第四篇:malloc, heap & the program break](http://blog.coderhuo.tech/2017/10/18/Virtual_Memory_malloc_and_heap/)
- malloc通过调用brk或sbrk增加program break的值

* video: [Call Stack](https://www.youtube.com/watch?v=5xUDoKkmuyw): 生動地解釋函式之間的關聯
- 直播影片中有不使用 gcc 便可觀察記憶體使用的演示
```shell
$ sudo cat /proc/1/maps | less
55cff6602000-55cff678b000 rw-p [heap]
7fff7e13f000-7fff7e160000 rw-p [stack]
```
#### 從遞迴學習 function call
1. `infinite.c`
```cpp
int func() {
static int count = 0;
return ++count && func();
}
int main() {
return func();
}
```
用 GDB 執行和測試,記得加上 `-g`:
```shell
$ gcc -o infinite infinite.c -g
$ gdb -q infinite
Reading symbols from infinite...done.
(gdb) r
Starting program: /tmp/infinite
Program received signal SIGSEGV, Segmentation fault.
0x00000000004004f8 in func () at infinite.c:3
3 return ++count && func();
(gdb) p count
$1 = 524032
```
:::warning
* 出現 Segmentation fault ( 使用到錯誤的記憶體區域 )
* 但又沒有使用指標,哪裡出問題?
* 【答案】上面的遞迴式沒有停下來的時候,會不斷的呼叫自己 ( 占用 stack )
* 直到 記憶體的 stack 不夠用
* Segmentation fault
:::
:::success
* 觀察 UNIX Process 中的 stack 空間:
```shell
$ sudo cat /proc/1/maps | grep stack
7fff7e13f000-7fff7e160000 rw-p 00000000 00:00 0 [stack]
```
* 60000~Hex~ - 3f000~Hex~ = 21000~Hex~ = 135168~Dec~
135168 * 4 = 540672
* 這跟前面的數字很接近!
* 函式就是「做好」與「做滿」
:::
2. 加入 參數 ( parameter )
```cpp
int func(int x) {
static int count = 0;
return ++count && func(x++);
}
int main() {
return func(0);
}
```
將得到:
```shell
Program received signal SIGSEGV, Segmentation fault.
0x0000000000400505 in func (x=1) at infinite.c:3
3 return ++count && func(x++);
(gdb) p count
$1 = 262016
```
:::warning
* 沒有解決 函式不斷呼叫自己的問題,但得到一個有趣的結果
* count 由 524032 減少到 262016
* 參數 ( parameter ) 占用 stack
:::
3. 加入 Local variable
```cpp
int func(int x) {
static int count = 0;
int y = x; // local var
return ++count && func(x++);
}
int main() {
return func(0);
}
```
將得到以下:
```shell
Program received signal SIGSEGV, Segmentation fault.
0x00000000004004de in func (x=<error reading variable: Cannot access memory at address 0x7fffff7fefec>) at infinite.c:1
1 int func(int x) {
(gdb) p count
$1 = 174677
```
:::warning
* 沒有解決 函式不斷呼叫自己的問題,但又得到一個有趣的結果
* count 由 262016 減少到 174677
* 參數 ( parameter ) 占用 stack
* Local variable 也占用 stack
:::
* stack 裡面有
* x (parameter)
* y (local variable)
* return address
:::info
* return value 會存放在 暫存器 ( e.g. $v0, $v1 in MIPS )
* 那如果回傳值為 `struct` , 暫存器塞不下怎麼辦?
【解答】 將 `struct`所在位址 存入 暫存器
:::
- [ROP (Return Oriented Programming)](https://yojo3000.github.io/CTF/ROP-Return-Oriented-Programming/)
- 該技術允許攻擊者在安全防禦的情況下執行代碼
- stack 和 heap 裡的程式碼都是 rw- ( 可讀可寫不可執行 )
- 幹壞事是進步的原動力
#### 資安問題 : stack-based buffer overflow
* [CVE-2015-7547](https://access.redhat.com/security/cve/cve-2015-7547)
> vulnerability in glibc’s DNS client-side resolver that is used to translate human-readable domain names, like google.com, into a network IP address. [ [解說](http://thehackernews.com/2016/02/glibc-linux-flaw.html) ]
* [Buffer Overflow : Example of Using GDB to Check Stack Memory](http://www.cs.ucf.edu/~czou/CAP6135-12/bufferOverFlow-gdb-example.ppt)
準備 `gdb-example.c`,其內容為:
```cpp
#include <stdio.h>
void foo(char *input) {
int a1 = 11;
int a2 = 22;
char buf[7];
strcpy(buf, input);
}
void main(int argc, char **argv) {
foo(argv[1]);
}
```
編譯,記得加上 `-g` 和 `-m32`
用 i686 架構執行 GDB:
```shell
$ setarch i686 -R gdb -q ./gdb-example
(gdb) break 6
Breakpoint 1 at 0x804847a: file gdb-example.c, line 6.
(gdb) run “whatever”
Starting program: /tmp/gdb-example "whatever"
Breakpoint 1, foo (input=0xffffd406 "whatever") at gdb-example.c:6
6 strcpy(buf, input);
```
觀察 stack 內容:
```shell
(gdb) info frame
Stack level 0, frame at 0xffffd180:
eip = 0x8048490 in foo (gdb-example.c:6); saved eip = 0x80484da
called by frame at 0xffffd1b0
source language c.
Arglist at 0xffffd178, args: input=0xffffd40c "whatever"
Locals at 0xffffd178, Previous frame’s sp is 0xffffd180
Saved registers:
ebp at 0xffffd178, eip at 0xffffd17c
(gdb) x &a1
0xffffd15c: 0x0000000b
(gdb) x &a2
0xffffd160: 0x00000016
(gdb) x buf
0xffffd165: 0x44f7f9c0
(gdb) x 0xffffd160
0xffffd160: 0x00000016
```
...自己玩
#### 藏在 Heap 裡的細節
* ==free() 釋放的是 pointer 指向位於 heap 的連續記憶體==
* 而非 pointer 本身佔有的記憶體 (`*ptr`)。
1. 舉例來說:
```cpp
#include <stdlib.h>
int main() {
int *p = (int *) malloc(1024);
free(p);
free(p);
return 0;
}
```
編譯不會有錯誤,但運作時會失敗:
```
*** Error in './free': double free or corruption (top):
0x000000000067a010 ***
```
:::info
* **`void free (void* ptr);`**
* Deallocate memory block
* A block of memory previously allocated by a call to `malloc`, calloc or realloc is deallocated, making it available again for further allocations.
* If `ptr` does not point to a block of memory allocated with the above functions, it causes undefined behavior.
* ==If `ptr` is a null pointer, the function does nothing.==
- 由於 alignment 議題,`malloc()` 可能會配置比預期還多的記憶體
* 參考 記憶體對齊 筆記
:::
2. 倘若改為以下:
```cpp
#include <stdlib.h>
int main() {
int *p = (int *) malloc(1024);
free(p);
p = NULL;
free(p);
return 0;
}
```
則會編譯和執行都成功。
* 為了防止對同一個 pointer 作 free() 兩次的操作,而導致程式失敗,
==`free()` 後應該設定為 `NULL`==。
:::warning
* 為什麼 glibc 可以偵測出上述程式的 "double free or corruption" 呢?
:::
...影片後面老師有試玩
#### malloc / free
**在 GNU/Linux 裡頭觀察 malloc**
事先安裝 gdb 和包含除錯訊息的套件
```shell
$ sudo apt install gdb gdb-dbg
```
GDB 操作:
```shell
$ gdb -q `which gdb`
Reading symbols from /usr/bin/gdb...
(gdb) start
...
Temporary breakpoint 1, main (argc=1, argv=0x7fffffffe4c8) at ./gdb/gdb.c:25
...
(gdb) p ((double(*)())pow)(2.,3.)
$1 = 8
(gdb) call malloc_stats()
Arena 0:
system bytes = 135168
in use bytes = 28000
Total (incl. mmap):
system bytes = 135168
in use bytes = 28000
max mmap regions = 0
max mmap bytes = 0
$2 = -168929728
(gdb) call malloc_info(0, stdout)
<malloc version="1">
<heap nr="0">
```
* glibc 提供了 `malloc_stats()` 和 `malloc_info()` 這兩個函式,可顯示 process 的 heap 資訊
* `malloc_trim()`
## [遞迴呼叫篇](https://hackmd.io/@sysprog/c-recursion?type=view)
*「[遞迴(recurse)只應天上有,凡人該當用迴圈(iterate)](http://coder.aqualuna.me/2011/07/to-iterate-is-human-to-recurse-divine.html)」*
* [遞迴 (Recursion)](https://notfalse.net/9/recursion)
* [Recursive Programming](https://www.cs.cmu.edu/~adamchik/15-121/lectures/Recursions/recursions.html)
#### 遞迴程式沒有你想像中的慢
* 最大公因數 (Greatest Common Divisor,縮寫 GCD)
典型的演算法為輾轉相除法,又稱歐幾里得算法 (Euclidean algorithm)
1. 遞迴的實作
```cpp
unsigned gcd_rec(unsigned a, unsigned b) {
if (!b) return a;
return gcd_rec(b, a % b);
}
```
2. 迭代的實作
```cpp
unsigned gcd_itr(unsigned a, unsigned b) {
while (b) {
unsigned tmp = b;
b = a % b;
a = tmp;
}
return a;
}
```
:::warning
* 迭代比遞迴多了 ==區域變數== 的使用
* 在 平行運算 ( 多核、雲端 等 ) 的環境下,為了追蹤這個 區域變數 ,會需要額外的空間來記錄,降低效能
:::
- 分析 clang/llvm 編譯的輸出 (參數 `-S -O2`),不難發現兩者轉譯出的 inner loop 的組合語言完全一樣:
```
LBB0_2:
movl %edx, %ecx
xorl %edx, %edx
divl %ecx
testl %edx, %edx
movl %ecx, %eax
jne LBB0_2
```
* 顯然遞迴版本的原始程式碼簡潔,而且對應於輾轉相除法的==數學定義==。
#### 尾端遞迴 (tail recursion)
* 這是實務上一種重要的遞迴種類,指的是具備:
1. 直接遞迴 (direct recursion)
2. 線性遞迴 (linear recursion)
3. 該 函式執行的最後一件事 為遞迴呼叫,且 只能是遞迴呼叫
* 其中,第三點尤其重要:
* 最後執行的內容,一定要豪乾淨的,
* 只有呼叫遞迴,不能做其他事!
:::warning
* 可將 遞迴途中的變數 包進 遞迴式的參數
* 達到 Tail Recursion 的模式
* 使 編譯器 能夠進行 Tail Call Optimization, TCO
:::
* Head recursion
#### 案例分析: 等效電阻
:::info
| | 公式 |
|:----:|:---------------------------------------------:|
| 串聯 | $r = r_1 + r_2$ |
| 並聯 | $\frac{1}{r} = \frac{1}{r_1} + \frac{1}{r_2}$ |
:::
```
r r r
-----###-----------###----------- . . . --------###------------- A
| | | | |
# # # # #
r # r # r # # r #
# # # # #
| | | | |
---------------------------------- . . . ------------------------ B
1 2 3 n - 1
```
可視為
```
r
----------###------------- A -------- A
| | |
# # #
R(r, n - 1) # r # ==> # R(r, n)
# # #
| | |
--------------------------- B -------- B
```
* 數學推導:
$$
\frac{1}{R(r,n)} = \frac1r + \frac1{R(r, n - 1) + r}
$$
* The recursive function is therefore:
$$ R(r,n)=
\begin{cases}
r & \text{if n = 1}\\
1 / (\frac1r + \frac1{R(r, n - 1) + r}) & \text{if n > 1}
\end{cases}
$$
* it is possible to show that
$$
R(r,n) = \frac{r F(2n - 1)}{F(2n)},
$$
where $F$ is the Fibonacci function.
```python
def circuit(n, r):
if n == 1:
return r;
else:
return 1 / (1 / r + 1 / (circuit(n - 1, r) + r))
```
#### 腦力激盪:數列輸出
1. 以下 C 程式的作用為何?
```cpp=
int p(int i, int N) {
return (i < N && printf("%d\n", i) && !p(i + 1, N))
|| printf("%d\n", i);
}
```
* 程式碼分析 :
```clike=2
(i < N && printf("%d\n", i) && !p(i + 1, N))
```
* `&&` 的運算規則為**左值優先**
* ==只要左值不成立,右值都不會執行==
* 若 `i` $\geq$ `N` ,不會印出 `i`,也不會呼叫 `p`
* 若 `i` < `N` ,`i` 會被輸出,接著會呼叫 `p`
* 換言之,遞迴成立條件是 `i` < `N`
:::info
* [C Operator Precedence](http://en.cppreference.com/w/c/language/operator_precedence)
* [printf(3)](https://linux.die.net/man/3/printf) 會回傳印出的字元數目,這裡一定回傳非零值
* 查詢 man page,對應到 GNU/Linux 的指令為 `man 3 printf`
:::
```clike=3
|| printf("%d\n", i)
```
* `||` 的運算規則為==當左值成立時,右值就不會執行==
* 因此 **`p` 前面的 `!` 很重要**。
* 因為 p 的回傳值一定是 true (由於 `printf` 一定回傳非零值),而為確保會執行到這第二個 `printf`,要將回傳值作 NOT,讓第一部份的結果為 false
* 如果去掉 NOT,則只會輸出 `i -> N`
:::info
把 `!p(i+1, N)` 的反相`!` 拿掉後,得到以下結果:
```
/* i = 1 , n = 5 */
1
2
3
4
5
```
:::
* 第二個 `printf` 要等 `p` 執行完畢才會被執行。
* 遞迴呼叫在實做層面來說,就是藉由 stack 操作,這裡一旦被 push 到 stack 印一次,被 pop 出來再印一次
* 綜合以上分析,我們可得知上述程式碼的作用為
**「印出 i -> N -> i 的整數序列,N 只會出現一次」**。
2. 延伸問題: 把 `&&` 前後的敘述對調,是否影響輸出?
從 `i < N && printf("%d\n", i)` 改為 `printf("%d\n", i) && (i < N)`
* 如果對調 `printf` 跟 `i < N` 則會**輸出 `i -> N N -> i` (N 出現兩次)**
* 因為 `printf` 會先被執行,不會受到 `i < N` 成立與否影響。
3. 延伸問題:`i` 和 `N` 組合的有效上下界為何?
* 不妨將原本程式碼改寫為以下:
```cpp
#include <limits.h>
#include <stdio.h>
int p(int i, int N) {
return (i < N && printf("%d\n", i) && !p(i + 1, N)) \
|| printf("%d\n", i);
}
int main() {
return p(0, INT_MAX);
}
```
* 在 Linux x86_64 環境編譯並執行後,會得到類似以下輸出: (數字可能會有出入)
```
261918
261919
261920
程式記憶體區段錯誤
```
* 這裡的 segmentation fault 意味著 stack overflow,遞迴呼叫時,每一層都有變數存放於 stack 中,每次呼叫也要保存回傳位址 (return address)
* 為了滿足 [x86_64 ABI / calling convention](https://en.wikipedia.org/wiki/X86_calling_conventions),
* 回傳位址佔 8 bytes,
* (int) `i` 和 (int) `N` 這兩個變數合計 8 bytes,
* 函式的區域變數 (給 `printf()` 用的 format string 的位置) 8 bytes,
* p 回傳值 int 佔 4bytes ,
* 總共 32 bytes。
* 計算過程: ( 假設 可用 stack size 為 8MB )
```
8MB = 8,388,608 bytes
8,388,608 / 32 = 262,144 次
```
* 綜合上述,推算出 `0 < N - i < 262144`
:::info
* 可用 `ulimit -s` 來改 stack size,預設是 8 MB,計算後可推得,每個 stack 大約佔用 32 bytes,N 的限制取決於 stack size 的數值。
* 延伸閱讀: [通過 ulimit 改善系統效能](https://www.ibm.com/developerworks/cn/linux/l-cn-ulimit/)
:::
#### [Fibonacci sequence](https://hackmd.io/nWwDmm64SyqmlhGpgNbbag?both#%E9%81%9E%E8%BF%B4%E7%A8%8B%E5%BC%8F%E8%A8%AD%E8%A8%88)
* 數學定義如下:
$F_n = F_{n-1}+F_{n-2},$
$F_0 = 0, F_1 = 1$
數列值:
| $F_0$ | $F_1$ | $F_2$ | $F_3$ |$F_4$|$F_5$|$F_6$|$F_7$|$F_8$|$F_9$|$F_{10}$|$F_{11}$|$F_{12}$|$F_{13}$|$F_{14}$|$F_{15}$|$F_{16}$|$F_{17}$| $F_{18}$|$F_{19}$|$F_{20}$|
| ----| ---- | ---- |---- |---- |---- |---- |---- |---- |---- |---- |---- |---- |---- |---- |---- |---- |---- |---- |---- |---- |
| 0| 1 |1|2|3|5|8|13|21|34|55|89|144|233|377|610|987|1597|2584|4181|6765|
1. 遞迴法 (Recursive)
* 將 Fibonacci 數列定義 轉為程式碼
```cpp
int fib(int n) {
if (n == 0) return 0;
if (n == 1) return 1;
return fib(n - 1) + fib (n - 2);
}
```
```graphviz
digraph hierarchy {
graph [nodesep="1"];
11 [label="Fib(5)" shape=box];
21 [label="Fib(4)" shape=box];
22 [label="Fib(3)" shape=box];
31 [label="Fib(3)" shape=box];
32 [label="Fib(2)" shape=box];
33 [label="Fib(2)" shape=box];
34 [label="Fib(1)=1" shape=box];
41 [label="Fib(2)" shape=box];
42 [label="Fib(1)=1" shape=box];
43 [label="Fib(1)=1" shape=box];
44 [label="Fib(0)=0" shape=box];
45 [label="Fib(1)=1" shape=box];
46 [label="Fib(0)=0" shape=box];
51 [label="Fib(1)=1" shape=box];
52 [label="Fib(0)=0" shape=box];
11 ->{21 22}
21 ->{31 32}
22 ->{33 34}
31 -> {41 42}
32 -> {43 44}
33 -> {45 46}
41 -> {51 52}
}
```
2. 非遞迴法 (Iterative)
* 縮減原先使用遞迴法的函式呼叫造成之執行時期開銷。
* 先討論基本方法。
```cpp
int fib(int n) {
int pre = -1;
int result = 1;
int sum = 0;
for (int i = 0; i <= n; i++) {
sum = result + pre;
pre = result;
result = sum;
}
return result;
}
```
* 我們可減少變數的使用:
```cpp
int fib(int n) {
int pre = -1;
int i = n;
n = 1;
int sum = 0;
while (i > 0) {
i--;
sum = n + pre;
pre = n;
n = sum;
}
return n;
}
```
3. Tail recursion
* 第一次 call function 後即開始計算值
* 大幅降低時間,減少 stack 使用量
```cpp
int fib(int n, int a, int b) {
if (n == 0) return a;
return fib(n - 1 , b, a + b);
}
```
```graphviz
digraph hierarchy {
nodesep=1.0 // increases the separation between nodes
node [fontname=Courier,shape=box] //All nodes will this shape and colour
"Fib(5,0,1)"->"Fib(4,1,1)"
"Fib(4,1,1)"->"Fib(3,1,2)"
"Fib(3,1,2)"->"Fib(2,2,3)"
"Fib(2,2,3)"->"Fib(1,3,5)"
"Fib(1,3,5)"->"return 5"
}
```
4. Q-Matrix
$$
A^1 =
\left(
\begin{array}{ccc}
1 & 1 \\
1 & 0 \\
\end{array}
\right)
= \left(
\begin{array}{ccc}
F_2 & F_1 \\
F_1 & F_0 \\
\end{array}
\right)
$$
$$
\begin{split}
A^{n+1} &= AA^n \\ &=
\left(
\begin{array}{ccc}
1 & 1 \\
1 & 0 \\
\end{array}
\right)
\left(
\begin{array}{ccc}
F_{n+1} & F_{n} \\
F_{n} & F_{n-1} \\
\end{array}
\right) \\ \\ &=
\left(
\begin{array}{ccc}
F_{n+1}+F_{n} & F_{n}+F_{n-1} \\
F_{n+1} & F_{n} \\
\end{array}
\right) \\ \\ &=
\left(
\begin{array}{ccc}
F_{n+2} & F_{n+1} \\
F_{n+1} & F_{n} \\
\end{array}
\right)
\end{split}
$$
* Divide and Conquer Method
$$
A^{2n+1} =A^{n+1}A^n
$$
```cpp
int **matrix_multiply(int a[2][2],int b[2][2]) {
int *t = malloc(sizeof(int) * 2 * 2);
memset(t, 0, sizeof(int) * 2 * 2)
for (int i = 0 ; i < 2 ; i ++ )
for (int j = 0 ; j < 2 ; j ++ )
for (int k = 0 ; k < 2 ; k ++)
t[i][j] += a[i][k] * b[k][j];
return t;
}
// 使用 Divide-and-Conquer 方法加速矩陣次方
int **matrix_pow(int a[2][2] , int n) {
if (n == 1) return a;
if (n % 2 == 0) {
int t[2][2];
t = matrix_pow(a , n >> 1);
return matrix_multiply(t , t);
}
int t1[2][2], t2[2][2];
t1 = matrix_pow(a, n >> 1);
t2 = matrix_pow(a, n >> 1 + 1);
return matrix_multiply(t1, t2);
}
```
```cpp
int fib(int n) {
if (n < = 0) return 0;
int A1[2][2] = { { 1 , 1 } , { 1 , 0 } };
int result[2][2];
result = matrix_pow(A1, n);
return result[0][1];
}
```
5. Fast doubling
$$
\begin{bmatrix}
1 & 1 \\
1 & 0
\end{bmatrix}^n =
\begin{bmatrix}
F(n+1) & F(n) \\
F(n) & F(n-1)
\end{bmatrix}
$$
$$
\begin{split}
\begin{bmatrix}
F(2n+1) \\
F(2n)
\end{bmatrix} &=
\begin{bmatrix}
1 & 1 \\
1 & 0
\end{bmatrix}^{2n}
\begin{bmatrix}
F(1) \\
F(0)
\end{bmatrix}\\ \\ &=
\begin{bmatrix}
1 & 1 \\
1 & 0
\end{bmatrix}^n
\begin{bmatrix}
1 & 1 \\
1 & 0
\end{bmatrix}^n
\begin{bmatrix}
F(1) \\
F(0)
\end{bmatrix}\\ \\ &=
\begin{bmatrix}
F(n+1) & F(n) \\
F(n) & F(n-1)
\end{bmatrix}
\begin{bmatrix}
F(n+1) & F(n) \\
F(n) & F(n-1)
\end{bmatrix}
\begin{bmatrix}
1 \\
0
\end{bmatrix}\\ \\ &=
\begin{bmatrix}
F(n+1)^2 + F(n)^2\\
F(n)F(n+1) + F(n-1)F(n)
\end{bmatrix}
\end{split}
$$
```cpp
int fib(int n) {
if (n == 0) return 0;
int t0 = 1; // F(n)
int t1 = 1; // F(n + 1)
int t3 = 1; // F(2n)
int t4; // F(2n+1)
int i = 1;
while (i < n) {
if ((i << 1) <= n) {
t4 = t1 * t1 + t0 * t0;
t3 = t0 * (2 * t1 - t0);
t0 = t3;
t1 = t4;
i = i << 1;
} else {
t0 = t3;
t3 = t4;
t4 = t0 + t4;
i++;
}
}
return t3;
}
```
* 演算法比較
| 方法 | 複雜度 |
|:-------------- |:-----------:|
| Recursive | $O(2^n)$ |
| Iterative | $O(n)$ |
| Tail Recursion | $O(n)$ |
| Q-Matrix | $O(log\ n)$ |
| Fast Doubling | $O(log\ n)$ |
* [An integer formula for Fibonacci numbers](https://blog.paulhankin.net/fibonacci/)

#### 腦力激盪:字串反轉
- 用 C 語言實做 `char *reverse(char *s)`,反轉 NULL 結尾的字串,
限定 **in-place** 與 **遞迴**
* 先思考實做 swap 的技巧
* 參考 [Bitwise 筆記](https://hackmd.io/GSuuqlufRHGzar6WEFFPPg?both#4-XOR-swap)
* 解法 I : 一直 swap '\0'之前的character
* 演算法描述:
1. 先把首尾互換

2. 把尾端和'\0'互換

3. 重複遞迴,直到'\0'在中間

4. 層層把'\0'換回最尾即可

:::spoiler 過程示意
:::info
a b c ==d== ==e== -> a b c ==e== ==d==
a b ==c== ==e== d -> a b ==e== ==c== d
a b e ==c== ==d== -> a b e ==d== ==c==
a ==b== ==e== d c -> a ==e== ==b== d c
a e b ==d== ==c== -> a e b ==c== ==d==
a e ==b== ==c== d -> a e ==c== ==b== d
a e c ==b== ==d== -> a e c ==d== ==b==
==a== ==e== c d b -> ==e== ==a== c d b
e a ==c== ==d== b -> e a ==d== ==c== b
e a d ==c== ==b== -> e a d ==b== ==c==
e ==a== ==d== b c -> e ==d== ==a== b c
e d a ==b== ==c== -> e d a ==c== ==b==
e d ==a== ==c== b -> e d ==c== ==a== b
e d c ==a== ==b== -> e d c ==b== ==a==
:::
:::
```cpp
static inline void swap(char *a, char *b) {
*a = *a ^ *b; *b = *a ^ *b; *a = *a ^ *b;
}
char *reverse(char *s) {
if((*s == '\0') || (*(s + 1) == '\0'))
return NULL;
reverse(s + 1);
swap(s, (s + 1));
if (reverse(s + 2) != '\0')
reverse(s + 2);
reverse(s + 1);
}
```
* 程式碼解析:
* 假設我們要反轉:
$$
5\space 4\space 3\space 2\space 1\space
$$
1. $reverse(s + 1)$ 先反轉後4個:
$$
5\space 1\space 2\space 3\space 4\space
$$
2. 然後再把1跟5對調:
$$
1\space 5\space 2\space 3\space 4\space
$$
3. 為了讓後四個能再利用$reserve(s + 1)$反轉,我們必須先將後三個調轉,
* 也就是調用$reverse(s+2)$:
$$
1\space 5\space 4\space 3\space 2\space
$$
4. 這樣一來我們就能調用$reverse(s+1)$來調轉後四個:
$$
1\space 2\space 3\space 4\space 5\space
$$
* 因此,$reverse(s)$可以拆成:
* $reverse(s+1)$ -> $swap(s, s+1)$ -> $reverse(s+2)$ -> $reverse(s+1)$
- 缺點:時間複雜度為 $$ T(n) = O(n^2) $$
* 解法 II : 計算字串長度時,即可交換字元
```cpp
int rev_core(char *head, int idx) {
if (head[idx] != '\0') {
int end = rev_core(head, idx + 1);
if (idx > end / 2) // 走到中間
swap(head + idx, head + end - idx);
return end;
}
return idx - 1; // 回傳 字串長度
}
char *reverse(char *s) {
rev_core(s, 0);
return s;
}
```
* 時間複雜度降為 $$ T(n) = O(n) $$
#### 案例分析: 類似 find 的程式
* 給定 [opendir(3)](http://man7.org/linux/man-pages/man3/opendir.3.html) 與 [readdir(3)](http://man7.org/linux/man-pages/man3/readdir.3.html) 函式,用遞迴寫出類似 [find](https://man7.org/linux/man-pages/man1/find.1.html) 的程式
* find 的功能:列出包含目前目錄和其所有子目錄之下的檔案名稱
:::info
* DIR *opendir(const char *name);
* struct dirent *readdir(DIR *dirp);
* dirent = direct entry
:::
:::warning
* opendir 回傳的型態為 pointer to DIR
* 為什麼不 回傳 pointer to dirent 就好 ?
* 反而是 先回傳 pointer to DIR , 然後再帶入 readdir ,最後再從回傳的 pointer to dirent 得到想要的資料
【解答】
* DIR 結構 會根據不同的作業系統及檔案系統 而有不同的落差
* dirent 結構 不論哪種環境下 定義都相同
* 因此,我們先用 opendir 確認好 DIR 的結構
* 再帶入 readdir 取出 我們要的資料
- 可兼顧 跨平台的差異 及 效能
:::
```cpp
#include <sys/types.h>
#include <dirent.h>
void list_dir(const char *dir_name)
{
DIR *d = opendir(dir_name);
if (!d) return; /* fail to open directory */
while (1) {
struct dirent *entry = readdir(d); // 下一層
if (!entry) break;
const char *d_name = entry->d_name;
printf ("%s/%s\n", dir_name, d_name);
if ((entry->d_type & DT_DIR) // 檢查 型態是否為 目錄
&& strcmp(d_name, "..") && strcmp(d_name, ".")) {
char path[PATH_MAX];
int path_length = snprintf(path, PATH_MAX,
"%s/%s", dir_name, d_name);
printf ("%s\n", path);
if (path_length >= PATH_MAX) return; // 檢查路徑名稱是否太長
/* Recursively call "list_dir" with new path. */
list_dir (path);
}
}
if (closedir (d)) return;
}
```
* 練習: 如何連同檔案一併列印?
* 練習:上述程式碼實做有誤,額外的 `.` 和 `..` 也輸出了,請修正
source: [rd.c](https://www.lemoda.net/c/recursive-directory/rd.c)
#### 案例分析: Merge Sort
* [Program for Merge Sort in C](http://www.thecrazyprogrammer.com/2014/03/c-program-for-implementation-of-merge-sort.html): 內含動畫
* [非遞迴的版本](http://stackoverflow.com/questions/1557894/non-recursive-merge-sort)


* [Merge Sort](http://www.personal.kent.edu/~rmuhamma/Algorithms/MyAlgorithms/Sorting/mergeSort.htm): 複雜度分析
#### 函數式程式開發
* 進行中: [MapReduce with POSIX Thread](https://hackmd.io/s/Hkb-lXkyg)
* Functional programming 在 [concurrency 環境](https://hackmd.io/s/H10MXXoT) 變得日益重要
* 如何透過軟體,讓 多核環境 更有效率
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet