---
title: "平面幾何 II"
path: "平面幾何 II"
---

{%hackmd @RintarouTW/About %}

# 平面幾何 II

## 圓 (Circle)

圓，等距也。

### 直角三角形

共斜邊即共圓

<iframe src="https://rintaroutw.github.io/fsg/test/right-triangles-in-circle.svg" width="768" height="600"></iframe>

### 圓內接四邊形 (Cyclic quadrilateral)

1. 對角線將四邊形切成兩組相似三角形
2. 托勒密定理 (Ptolemy Theorem)：對角線乘積=兩組對邊乘積和

<iframe src="https://rintaroutw.github.io/fsg/test/Ptolemy.svg" width="768" height="600"></iframe>

$$
\angle{ADB}=\angle{ACB}\ (對同弧 AB)\\
令 \angle{EBC}=\angle{ABD}, 則\\
\triangle{ABD}\simeq\triangle{EBC}\\
\implies \overline{CE}:\overline{AD} = \overline{BC}:\overline{BD}\\
\implies \overline{AD}\times\overline{BC}=\overline{CE}\times\overline{BD}
$$
$$
又 \cases{
\angle{BAC}=\angle{BDC}\ (對同弧 BC)\\
\angle{ABE}=\angle{DBC}\\
}\\
則\triangle{ABE}\simeq\triangle{DBC}\\
\implies \overline{AE}:\overline{CD} = \overline{AB}:\overline{BD}\\
\implies \overline{AB}\times\overline{CD}=\overline{AE}\times\overline{BD}
$$

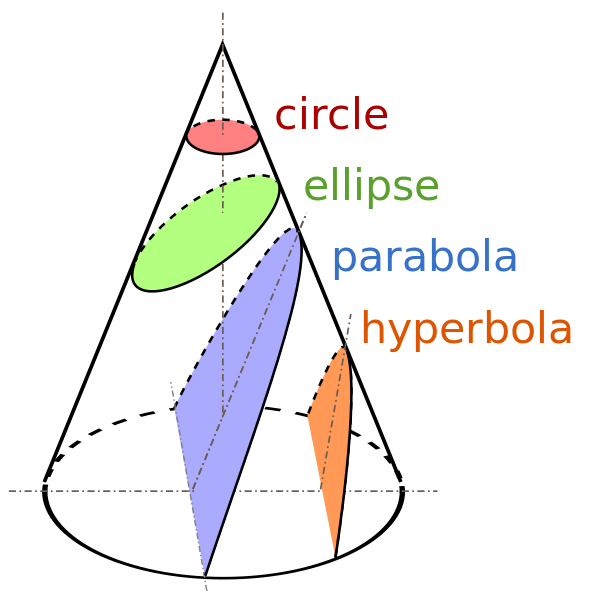
## 一點一線間的藝術 (圓錐曲線/切面 - Conic Section)

設 F 為定點， L 為定直線， e 為正常數，稱滿足$\frac {|PF|}{|PL|} = e$ 的動點 P 的軌跡為圓錐曲線。

其中 F 為其焦點， L 為準線， e 為離心率。


<center>圓錐曲線/切面 (Conic Section) 此圖來自<a href="https://en.wikipedia.org/wiki/Conic_section">維基</a></center>



## 拋物線 (<span class="synth">Parabola</span>)

動點 P 與 F, L 等距 (e = 1)，軌跡為拋物線。

拋物線上的點到焦點的距離等於該點到準線的距離。

## 橢圓 (<span class="synth">Ellipse</span>)

0 < e < 1 ，則為橢圓。

橢圓上的點到兩個焦點的距離和等於長軸長

正圓可視為橢圓之特例

## 雙曲線 (<span class="synth">Hyperbola</span>)

e > 1 ，則為雙曲線。

雙曲線上的點到兩個焦點的距離之差的絕對值等於貫軸長（2a）。

## 貝茲曲線 (<span class="synth">Bézier Curves</span>)

### 一次(線性)

$$
{\mathbf {B}}(t)={\mathbf {P}}_{0}+({\mathbf {P}}_{1}-{\mathbf {P}}_{0})t=(1-t){\mathbf {P}}_{0}+t{\mathbf {P}}_{1}{\text{ , } }t\in [0,1]
$$


### 二次 (TTF, Adobe Flash)

$$
{\mathbf {B}}(t)=(1-t)^{{2}}{\mathbf {P}}_{0}+2t(1-t){\mathbf {P}}_{1}+t^{{2}}{\mathbf {P}}_{2}{\text{ , }}t\in [0,1]
$$


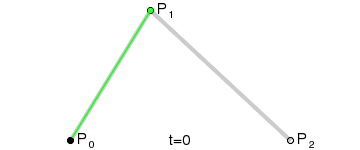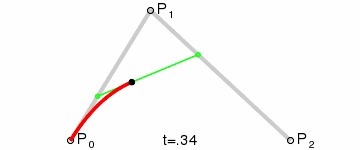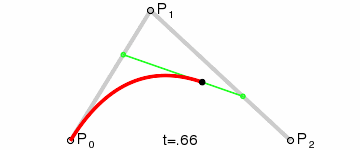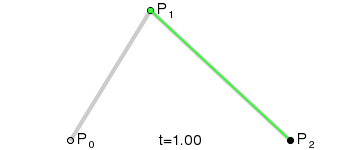
$P_0, P_2$ 為 Anchor Point; $P_1$ 為 Control Point

### 三次 (PostScript, Illustrator, etc...)

$$
{\mathbf {B}}(t)={\mathbf {P}}_{0}(1-t)^{3}+3{\mathbf {P}}_{1}t(1-t)^{2}+3{\mathbf {P}}_{2}t^{2}(1-t)+{\mathbf {P}}_{3}t^{3}{\text{ , }}t\in [0,1]
$$


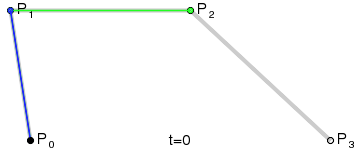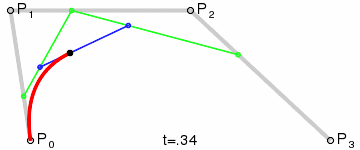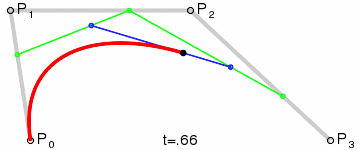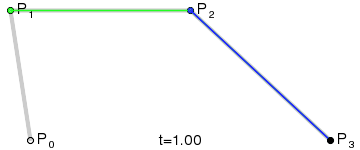
$P_0, P_3$ 為 Anchor Point; $P_1, P_2$ 為 Control Point

# 平行四邊形 (Parallelogram)

**由兩全等三角形組成**

<iframe src="https://rintaroutw.github.io/fsg/test/Parallelogram.svg" width="768" height="600"></iframe>

任意 $\triangle$ ABC，延任一邊平行可作一全等三角形 (或以任一邊中點為中心旋轉 $180^\circ$)，共三邊則可作另三個全等三角形，組合可成三種平行四邊形。

反過來看，$\triangle$ DEF 之各邊中點連線即為 $\triangle$ ABC。

**由兩梯形組成**

<iframe src="https://rintaroutw.github.io/fsg/test/Trapezoid.svg" width="768" height="600"></iframe>

**對角線分割成兩組全等三角形**

即對角線相互平分；反之，若一四邊形對角線相互平分，亦可證之為平行四邊形。

**對角線平方和**

對角線平方和 = 各邊長平方之和

**鄰角互補**

兩全等三角形 $180^\circ$ 相對，三角形內角合為 $180^\circ$。

如上圖，$\angle DCB = \angle ABC$，則 $\angle DCA = \angle DCB + \angle ACB = \angle ABC + \angle ACB$，故

$$
\angle DCA + \angle CAB = \angle ABC + \angle ACB + \angle CAB = 180^\circ (\triangle ABC 內角和)
$$

做高(間距)，$90^\circ + \theta + 90^\circ - \theta = 180^\circ$。

鄰角互補，亦可證兩線平行，兩條件等價。

$$
鄰角互補\iff 兩線平行
$$

**面積**

平行四邊形之高為對邊間距，面積等於同底同高之矩形。

反之，等高即等距，故等底即等積，亦積之比同底之比。

## 矩形 (Rectangle)

矩形為平行四邊形之特例，對角線既相互平分外，也等長。

## 梯形面積 (Trapezoid)

copy 再轉，組成平形四邊形，其邊長 = 上底+下底，寬為高，面積為

$$
(上底+下底)\times高
$$

因為一半面積是 copy 來的，所以實際梯形是平形四邊形的一半，要除 2。

$$
梯形面積 = (上底+下底)\times高 \div 2
$$

###### tags: `math` `geometry`